Hamming korrekciós kódok
A Hamming kódok építése a W blokk (az egyes szimbólumok számának) paritásának ellenőrzésén alapul, a kódblokk információblokkjában.
Pontosítsuk a paritásellenőrzés ötletét a legegyszerűbb korrekciós kód példájával, amelyet paritásellenőrző kódnak vagy paritásos (egyenlőségi) ellenőrzésnek nevezzük.
Ebben a kódban egy további bitet adunk hozzá a nem redundáns primer bináris m-bites kód (paritásellenőrző szimbólum, úgynevezett csekk vagy csekk) kódszavakhoz. Ha a szimbólumok „1” az eredeti kódszó még a további mentesítési generál pilotszimbólum 0, és ha a szimbólumok „1” páratlan, akkor további alakítási mentesíti szimbólum 1. Ennek eredményeként a szimbólumok teljes száma „1” semmilyen átküldött kódszó mindig egyenletes lesz.
Így a hitelesítési szimbólum létrehozásának szabálya a következő:
,
ahol i a megfelelő információs szimbólum (0 vagy 1), m az összes számuk, és a "" művelet alatt itt és alul a mod2 hozzáadása. Nyilvánvaló, hogy egy további bit hozzáadásával az eredeti forráskód kombinációinak számához viszonyítva az összes kombináció számát felére növeljük, és a paritási feltétel minden kombinációt elválasztja a megengedett és a megoldatlan formátumok közül. A paritásellenőrzéssel ellátott kód lehetővé teszi egyetlen hiba észlelését kódkombináció fogadásakor, mivel egy ilyen hiba megsérti az egyenlőségi feltételt, ha az engedélyezett kombinációt tiltottá alakítja.
A kapott kombináció helyességének kritériuma a kód összes n szimbólumának mod2 summációjának S egyenletének egyenlősége, beleértve a k1 ellenőrző szimbólumot is. Egy hiba jelenlétében S az 1:
.
Ez a kód (m + 1, m) - kód, vagy (n, n -1) - kód. A minimális kód távolsága két (dmin = 2), ezért nem lehet hibát kijavítani. Egy egyszerű paritásellenőrző kódot csak egy hiba észlelésére (de nem helyes) észlelhet.
A további ellenőrző számok számának növelése és a k ellenőrző szimbólumok létrehozása bizonyos szabályok szerint. 0 vagy 1 értékkel egyenlő, akkor erősítheti a kód korrekciós tulajdonságait, így nemcsak a hibák észlelését, hanem javítását is lehetővé teszi. Ez a Hamming kódok megalkotásának alapja.
Hamming kódok. Tekintsük ezeket a kódokat, amelyek lehetővé teszik egy hiba kijavítását egy közvetlen leírás használatával. A k = 3,4,5 ellenőrző szimbólumok minden egyes számához tartozik egy klasszikus Hamming kód a jelöléssel
azaz - (7.4), (15.11), (31.26) ...
Az m információs szimbólumok más értékeire az úgynevezett csonka (csonkolt) Hamming kódokat kapjuk. Tehát a MTK-2 nemzetközi távirat kódja. (9, 5), amely a klasszikus Hamming kóddal (15,11) csonka, mivel a kódok száma ebben a kódban csökken (rövidítve) 6-kal. Például vegye figyelembe a Hamming kódot (7.4) ), amely a 13.1 ábrán látható kódoló segítségével generálható és írható le. A legegyszerűbb formájában az adott négy (m = 4) információs szimbólumokat (i1, i2, i3, i4), feltételezzük, hogy vannak csoportosítva elején a kódszó, bár ez nem kötelező. Kiegészíteni ezeket információ szimbólumokat a paritás három (k = 3), kérve őket, a következő egyenletek paritás, amelyek által meghatározott megfelelő algoritmusok. Ismeretes, hogy a kód távolsága megegyezik az ellenőrzések minimális számával, amely magában foglalja az információs szimbólumot és az egyiket. A vizsgált kódban dmin. Ezért minden információs szimbólumnak legalább két ellenőrzést kell beírnia. Határozza meg a paritásszimbólumok kialakulásának szabályát az alábbiak szerint:
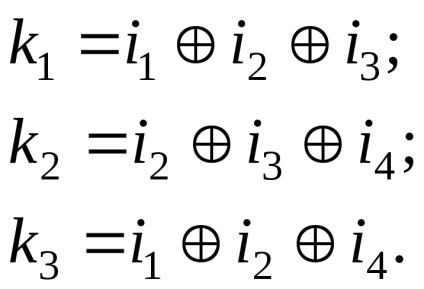
A 13.3 ábrán látható kiegyenlítési szimbólumok értékeinek meghatározására szolgáló algoritmussal összhangban a Hamming kód összes lehetséges 16 kódszava (7.4.) Szerepel.
Az 1. ábrán. A 13.2 ábra bemutatja a (7.4) - Hamming kód dekódoló áramkörét, amelynek bemenete egy kódszó
.
Az aposztróf azt jelenti, hogy egy szó bármely szimbóluma eltorzulhat az átviteli csatornán belüli interferenciával.
A dekóderben a hibajavító üzemmódban egy sorrendet állítunk elő:

A három karakteres sorozatot (s1, s2, s3) szindrómának nevezik. A "szindróma" kifejezést az orvostudományban is használják, ahol egy adott betegségre jellemző tünetek kombinációját jelöli. Ebben az esetben az S = (s1, s2, s3) szindróma a kódcsoport megfelelő szimbólumainak paritásvizsgálatának eredménye, és egy bizonyos hibakonfigurációt (hibavektor) jellemez.
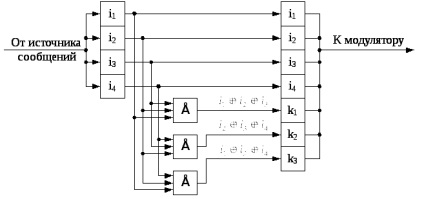
Ris.13.1. Coder egy egyszerű (7.4) - Hamming kódot
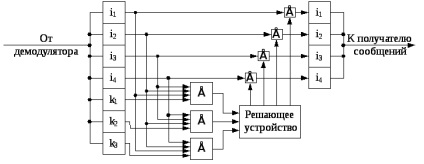
Ris.13.2. Dekóder egyszerű (7.4) - Hamming kód
Így a kód (7.4) lehetővé teszi az összes egyetlen hiba kijavítását. Egy egyszerű ellenőrzés azt mutatja, hogy mindegyik hiba sajátos szindrómával rendelkezik. Lehetőség van egy ilyen digitális hibajavító (szindróma dekóder) létrehozására, amely a megfelelő szimbólumot a megfelelő szindrómában a kapott kódcsoportban korrigálja. Korrekció után a ki ellenõrzõ szimbólumok nem adhatók ki a dekóder kimenetére (13.2 ábra). Két vagy több hiba meghaladja a Hamming korrekciós kódjait, és a dekódoló hibás. Ez azt jelenti, hogy helytelen javításokat végez és torz információs szimbólumokat hoz létre.
Az ilyen korrekciós kód megalkotásának gondolata természetesen nem változik, ha a szimbólumok helyzetét átrendezi a kódszavakban. Minden ilyen változatot szintén (7,4) Hamming kódnak neveznek.
A Hamming kiterjesztett kódjai a dmin = 3 kódok hozzáadásával keletkeznek az egyes paródiákkód-kombinációk általános ellenőrzéséhez. egy másik ellenőrző szimbólum. Ez lehetővé teszi a minimális kód távolságának növelését a dmin = 4 értékig.
A letöltés folytatásához össze kell gyűjtened a képet: