Magasabb matematika
Teszteld a munkaszámot 3
A gazdasági jellegű levelező tanfolyamokon
1. Két kockát dobnak. Mi a valószínűsége annak, hogy a pontok mennyisége 7 lesz?
2. Tegyük fel, hogy egy torpedónál a valószínűség a cél eléréséhez 0,7. Mi a valószínűsége annak, hogy három torpedó el fog süllyedni egy hajót, ha egy torpedó eltalálja a fulladás célját?
3. A kollektor 3 db dobozdarabot kapott az 1. üzemszámmal és 2 db 2-es gyártmányú dobozdarabokkal. Az 1-es számú növény szabványosságának valószínűsége 0,8, a 2. növény pedig 0,9. A gyűjtő a véletlenszerűen kiválasztott dobozból kivette az elemet. Keresse meg annak valószínűségét, hogy a szabványos részt kivonják.
4. Problémák megoldása a Bernoulli-képlet és a Moore-Laplace tétel segítségével.
a) Üzenet továbbítása esetén az egyik megjelölés torzulási valószínűsége 0,1. Mi ennek a valószínűsége. hogy egy 10 karakterből álló üzenet nem tartalmaz több mint 3 torzítást?
b) 400 fát ültettek. Az egyetlen fa túlélésének valószínűsége 0,8. Keresse meg azt a valószínűséget, hogy a túlélő fák száma: 1) 300, 2) nagyobb, mint 310, de kevesebb mint 330.
5. A lehetséges értékek listáját adják diszkrét értékek: x1 = -2, x2 = 1, x3 = 4, és ez az elvárás a velichinyM [X] = 2,5 és a kvadrataM [X 2] = 10,3. Keressétek egy X véletlen változó elosztási törvényét.
6. Egy folyamatos X véletlen változót egy eloszlásfüggvény adja
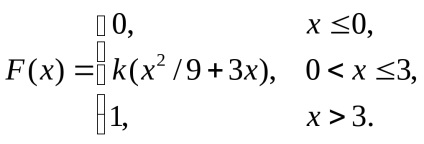
Keresse meg: a) a k paraméter; b) matematikai várakozás; c) diszperzió.
7. Ismerjük az a = 10 matematikai várakozást és a normál eloszlású X véletlen változó = 4 szórását. Határozza meg a következő valószínűségét: a) az adott értéknek egy adott intervallumban való leesése (5, 9); b) ennek a mennyiségnek a eltérése a matematikai várakozástól nem több mint na.
8. Egy mintát kivonunk az általános populációból, amelyet intervallumváltozat sorozat formájában ábrázolunk. a) Feltételezve, hogy a lakosság normális eloszlású, építésére megbízhatósági intervallum elvárás bizalommal veroyatnostyu = 0,95. b) Számítsuk ki a együtthatói ferdeség és csúcsossága, egy egyszerűsített számítási módszer, és hogy a megfelelő formában az eloszlási függvény a népesség feltételezések. c) A Pearson-kritérium alkalmazásával teszteljük a populáció normális eloszlásának hipotézisét = 0,05 szignifikancia szinten.
Magasabb matematika
Teszteld a munkaszámot 3
A gazdasági jellegű levelező tanfolyamokon
10. lehetőség
1. Öt terepi rádióállomás engedélyezett a gyakorlat során 6 rádióhullám működtetésére. A hullámválaszték minden állomáson véletlenszerű. Keresse meg annak a valószínűségét, hogy különböző rádióhullámokat fognak használni.
3. Az első doboz 20 darabot tartalmaz, amelyek közül 15 standard; a második - 30 részből 24 szabványos; a harmadik - 10 részből 6 szabványos. Keresse meg azt a valószínűséget, hogy véletlenszerűen a véletlenszerűen kihúzott dobozból kivont részlet standard.
4. Problémák megoldása a Bernoulli-képlet és a Moore-Laplace tétel segítségével.
a) Az esemény bekövetkezésének valószínűsége az öt független kísérlet mindegyikében 0,2. Határozza meg az esemény előfordulásának valószínűségét legalább 3-szor.
b) E növényfajta csírázása 90%. Meg kell találni azt a valószínűséget, hogy a 900 elültetett vetőmagtól a csírázás száma: 1) egyenlő 800, 2) 805 és 820 között.
5. Az X diszkrét véletlen változónak csak két lehetséges értéke van: x1 és x2. ahol x1 6. Egy folyamatos X véletlen változót egy eloszlásfüggvény adja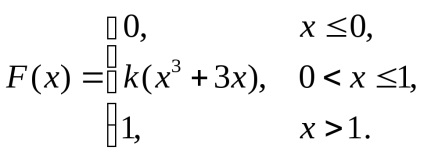
Keresse meg: a) a k paraméter; b) matematikai várakozás; c) diszperzió.
7. Ismerjük az a = 9 matematikai várakozást és a normál eloszlású X véletlen változó = 4 szórását. Keresse meg a következő valószínűségét: a) az értéket egy adott intervallumban (2, 10); b) ennek a mennyiségnek a eltérése a matematikai várakozástól nem több mint na.
8. Egy mintát kivonunk az általános populációból, amelyet intervallumváltozat sorozat formájában ábrázolunk. a) Feltételezve, hogy a lakosság normális eloszlású, építésére megbízhatósági intervallum elvárás bizalommal veroyatnostyu = 0,95. b) Számítsuk ki a együtthatói ferdeség és csúcsossága, egy egyszerűsített számítási módszer, és hogy a megfelelő formában az eloszlási függvény a népesség feltételezések. c) A Pearson-kritérium alkalmazásával teszteljük a populáció normális eloszlásának hipotézisét = 0,05 szignifikancia szinten.