Interpoláció algebrai polinomokkal

Az [a, b] intervallumban az f (x) függvény algebrai polinomjainak interpolációja P n (x) polinom, amelynek foka kisebb vagy egyenlő, mint n. amely az x0 interpolációs csomópontokon érkezik. x1. xn az f (xi) értékek:

P n (x i) = a 0 + a 1 x i + a 2 x i 2 +. + a n x i n = f (xi). i = 0. 1. n (x_) = a_ + a_x_ + a_x _ ^ +. + a_x _ ^ = f (x_), \ quad i = 0,1. n>

Nem zéró az xi minden páronkénti megkülönböztető értéke esetén. és az f függvény interpolációja az xi csomópontokon lévő értékekről a Pn (x) polinom segítségével mindig lehetséges és egyedi.

A kapott f (x) ≈ P n (x) (x)> interpolációs képletet gyakran alkalmazzuk az x függvény értékeinek hozzávetőleges számításához. az interpolációs csomópontokon kívül. Ebben az esetben az interpoláció szűk értelemben különböztethető meg, ha x ∈ [x 0. x n], x_ \ jobb]>. és extrapoláció. amikor x ∈ [a. b]. x ∉ [x 0. x n], x_ \ jobb]>

Tegyük fel, hogy n pontokat P 1 adtak meg az űrben. P n, P _, \ pontok, P_>. amelyek bizonyos koordináta rendszerben r 1. r 2. sugárvektorok vannak. r n _, \ mathbf _, \ pontok, \ mathbf _>.

Az interpoláció problémája a jelzett sorrendben áthaladó görbének kialakítása.

Pontos pontokon keresztül végtelen számú görbét lehet rajzolni, így az interpolációs probléma nem egyedülálló.

A paraméterezés és a rács bevezetése különféle módokon hajtható végre. Normális esetben egy egyenletes rácsot választunk, feltételezve, hogy a = 0. b = n - 1. t i = i - 1 = i-1. vagy, még előnyösebben, a kapcsoló tápvonal szegmensek pontok és paraméterértékeket a különbség t i + 1 - t i -t_> hogy intervallum hossza r i +1 - r i _- \ mathbf _>.

Az interpoláció egyik közös módja egy görbe alkalmazása n - 1 fokú t polinom formájában. vagyis függvényként

Ezek a feltételek a k> együtthatókhoz lineáris egyenletrendszerhez vezetnek

(1 t 1 t 1 2 ... t 1, n - 1 1 t 2 t 2 2 ... t 2 n - 1 ⋮ ⋮ ⋮ ⋮ 1 tntn 2 ... TNN - 1) (Anan - 1 ⋮ 1) = (r 1, r 2 ⋮ rn) 1t_t _ ^ \ ldots t _ ^ \\ 1t_t _ ^ \ ldots t _ ^ \\\ vdots \ vdots \ vdots \ vdots \\ 1t_t _ ^ \ ldots t _ ^ \ end> ​​\ mathbf _ \\\ mathbf _ \\\ vdots \\\ mathbf _ \ end> ​​= \ mathbf _ \\\ mathbf _ \\\ vdots \\\ mathbf _ \ end >>

Figyeljünk arra, hogy három egyenletrendszert kell megoldanunk: x esetén. y és z koordinátákat. Mindegyiknek ugyanaz a koefficiens mátrixa van, amely az r i_> pontok sugárvektorok értékei alapján kiszámítja a polinom együtthatóinak a k> vektorát. A mátrix meghatározója

W (t 1. t 2. ... T n) = | 1 t 1 t 1 2 ... t 1 n - 1 1 t 2 t 2 2 ... t 2 n - 1 ⋮ ⋮ ⋮ ⋮ 1 t n t n 2 ... t n n - 1 | = Π i. j. i> j (t i - t j), t_, \ ldots, t _) = 1t_t _ ^ \ ldots t _ ^ \\ 1t_t _ ^ \ ldots t _ ^ \\\ vdots \ vdots \ vdots \ vdots \\ 1t_t _ ^ \ ldots t _ ^ \ end> ​​= \ prod _ (t_-t _)>

Vandermonde meghatározónak nevezik. Ha a rács csomópontjai nem egyeznek meg, akkor a nullától eltérő, így az egyenletek rendszere megoldást kínál.

A közvetlen mátrix inverzió mellett az interpolációs polinom kiszámításának számos más módja is van. A polinom egyediségének köszönhetően a felvétel különböző formáiról beszélünk.

• Egy adott pontkészlet és egy paraméterhálózat esetében a görbe egyedileg van kialakítva.
• A görbe interpoláció, vagyis minden ponton áthalad.
• A görbe folyamatos sorrendben származik.

• A növekvő pontok számával növekszik a polinom sorrendje, és ezzel növeli a görbén lévő pont kiszámításához szükséges műveletek számát.
• Ahogy az interpolációs görbe pontjai nőnek, oszcillációk jelennek meg (lásd az alábbi példát).

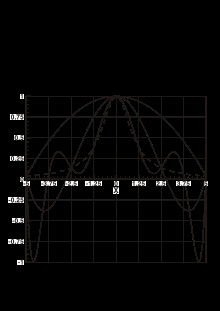
Interpoláció egy rácssorozaton. Runge példa.

Egy klasszikus példa (Runge), amely megmutatja az oszcillációk előfordulását egy interpolációs polinomban, az interpoláció a függvény egyenletes rácsán

amely az x i> pontokban az y i = 1 / (1 + x i 2) = 1 / (1 + x _ ^) értékeket veszi fel. Az ábra magának a függvénynek a grafikonjait (dash-pontozott vonal) és három interpolációs görbét mutatja n = 3. 5. 9:

• interpoláció a rácson x 1 = - 5. x 2 = 0. x 3 = 5 = -5, x_ = 0, x_ = 5> egy négyzetes parabola;
• interpoláció a rácson x 1 = - 5. x 2 = - 2,5. x 3 = 0. x 4 = 2,5. x 5 = 5 = -5, x_ = - 2,5, x_ = 0, x_ = 2,5, x_ = 5> a negyedik fokú polinom;
• interpoláció a rácson x 1 = - 5. x 2 = - 3.75. x 3 = - 2,5. x 4 = - 1,25. x 5 = 0. x 6 = 1,25. x 7 = 2,5. x 8 = 3,75. X 9 = 5 = -5, X _ = - 3,75, x _ = - 2,5, x _ = - 1,25, x_ = 0, x_ = 1,25, x_ = 2,5, x_ = 3,75, x_ = 5> - a polinom foka nyolc.

Az interpolációs polinom értékei, még a közbülső pontok közötti sima funkciók esetében is, erőteljesen eltérhetnek a funkció értékeitől.