Algoritmusok láthatatlan élek és arcok eltávolítására
A láthatatlan arcok eltávolítására szolgáló algoritmusok feltételesen két osztályra oszthatók, attól függően, hogy milyen elveik vannak a megvalósításukra. Az első osztály az objektumterületen dolgozó algoritmus. Ez azt jelenti, hogy egy adott arc láthatóságának megállapításához összehasonlítjuk a relatív pozícióját a háromdimenziós jelenet összes többi arcával. Legyen N az ábrák száma a háromdimenziós jelenetben. Ebben az esetben egy háromdimenziós jelenetet kell összeállítani, ezért össze kell hasonlítani az egyes arcok helyzetét a többiekkel, ami megköveteli a sorrendet
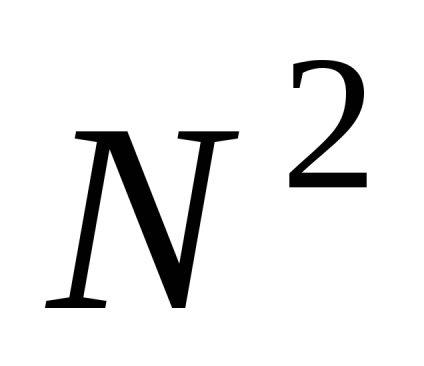
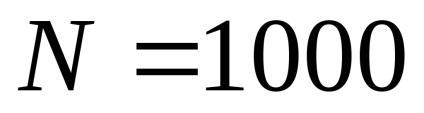
Az algoritmusok egy másik osztálya - amely a képterületen dolgozik - azon a ponton keresi a legközelebbi arcot, amely metszi a raszter adott pontján áthaladó látóvonalat. Mivel a raszter képernyőn lévő pontok száma meg van erősítve, akkor ennek az osztálynak az algoritmusa kevésbé érzékeny a háromdimenziós jelenetben lévő objektumok számának növekedésére. Legyen n a raszter képernyőn megjelenő pontok száma, majd a háromdimenziós jelenet létrehozásához szükséges műveletek száma
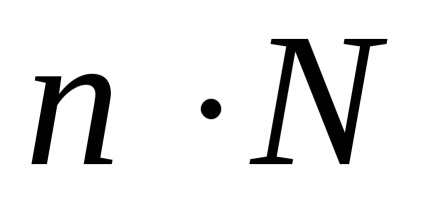

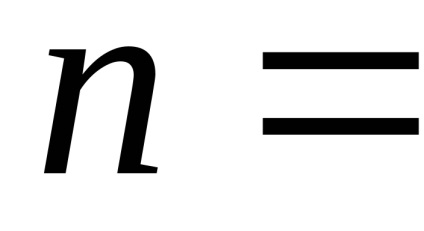
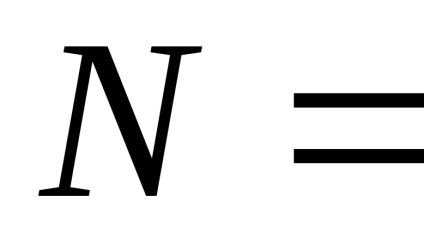
Tekintsünk egy algoritmust a láthatatlan arcok eltávolítására a z-buffer használatával, amely az egyik leggyakrabban használt a modern számítógépes grafikus alkalmazásokban. A képterületen működik, és olyan népszerű grafikus könyvtárakban használják, mint az OpenGL és a Direct3D.
Az algoritmus párhuzamos vetítéssel működik. Hagyja, hogy a kimeneti ablak vagy a képernyő mérete X pont legyen szélessége és Y pont magassága. Z-pufferként egy kétdimenziós téglalap alakú tömböt vezetünk be olyan méretekkel, amelyek egybeesnek a kimenettel vagy a képernyőablakkal, azaz X

Az algoritmus elején a végtelennek megfelelő értékek íródnak az z-pufferbe. Egy háromdimenziós objektum mindegyik arca, amelyet poligonként ábrázolnak, raszteres formává alakul át. Raszterbe bomláskor a sokszög minden egyes pontjára kiszámítjuk az z-koordináta értékét. Ha az z-koordináta kisebb, mint az aktuális érték az z-pufferben, a pont z-koordinátája az z-pufferbe van írva, és a pontot a képernyőn az aktuális sokszög színével rajzolja. Miután az összes sokszöget a raszterbe bontotta, a háromdimenziós jelenet képe épül fel.
Tekintsünk egy módszert a z-koordináták gyorsított számítására, amikor a poligonok raszterbe bomlanak. Adjuk meg a poligon által a térben kialakított sík egyenletét:.
A pont z-koordinátáját fejezzük ki :. Hadd legyen. Megtaláljuk a szomszédos pont z koordinátáját
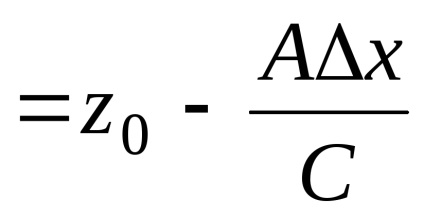
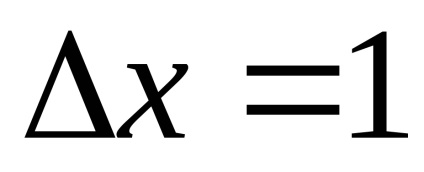
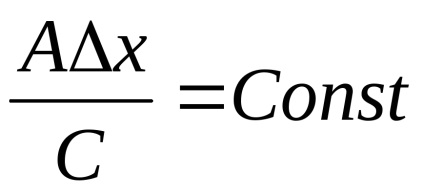
Az eljárás három fő lépésből áll:
Az összes sokszög elrendezése a legnagyobb z-koordinátákkal összhangban.
Minden olyan bizonytalanság feloldása, amely a poligonok z-shelljainak átfedésekor keletkezik.
Az egyes poligonok bitkép alakúvá alakítása, mely a legnagyobb z-koordináta csökkenésének sorrendjében keletkezik.
A legközelebbi sokszögek a raszteres alakzatokká alakulnak át a legutóbbiaknál, és bezárják a távolabbi sokszögeket, mivel azokat az előzőek tetején ábrázolták. Az 1. és 3. pont végrehajtása meglehetősen nyilvánvaló. Tekintsünk részletesebben a 2. pontra.
Hagyja, hogy a poligon P a megrendelés után a lista végén legyen, vagyis a legtávolabbi. Az összes poligonhéj átfedésben van a z-héjjal P-nek, el kell végezni az öt vizsgálat (lépcső) tesztjét. Ha egy bizonyos lépésnél pozitív válasz érkezik, akkor a P azonnal raszteres formává alakul.
x-A sokszögek poligonjai nem fedik egymást, így a poligonok nem átfedik egymást.
y-A sokszöghéjak nem fedik egymást, így a poligonok sem átfedik egymást.
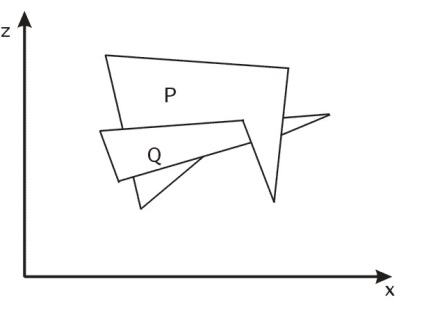
Teljesen a Q sík oldalán helyezkedik el, ami távolabb van a szempontból (ez a vizsgálat pozitív választ ad, amint azt a 36a. Ábra mutatja).
A Q teljesen a P sík oldalán helyezkedik el, amely közelebb áll a nézőponthoz. Ez a teszt pozitív választ ad, amint azt az 1. ábra mutatja. 36b).
Az xOy síkban levő sokszög-vetületek, vagyis a képernyőn, nem fedik egymást (ezt úgy határozzák meg, hogy összehasonlítják az egyik sokszög éleit a másik éleivel).
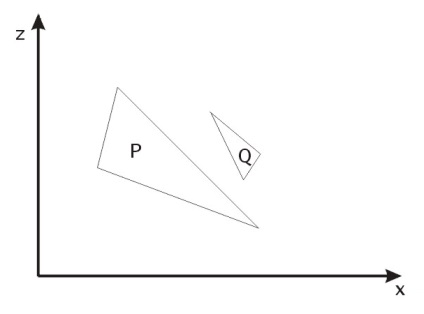
Ábra. 35.
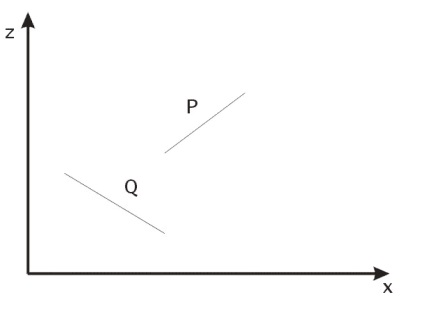
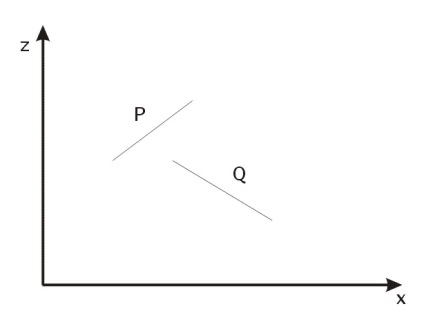
Ábra. 36. Háromszögek kölcsönös elrendezése az űrben.
Ha mind az öt teszt negatív választ kap, akkor P - valóban bezárja a Q.t. Ezután módosítsa a P és Q listákat a listában. Abban az esetben, ahogy a 37. ábrán látható, az algoritmust hurkoltuk.
A hurkok elkerülése érdekében korlátozás kerül bevezetésre: a lista végére (pl. Címkézett) áthelyezett sokszög nem helyezhető át. Ehelyett a P vagy Q poligont a másik síkja osztja két új sokszögre. Ez a két új sokszög a megfelelő helyen található a rendezett listában, és az algoritmus továbbra is működik.
Az univerzális algoritmusokkal ellentétben egy rendkívül speciális algoritmus a konvex testek láthatatlan arcainak eltávolítására teszi lehetővé a számítások gyorsabb elvégzését. Úgy működik, hogy a központi perspektíva vetülete. Vegyük fontolóra ennek az algoritmusnak a működését a 3. ábrán látható példában. 38.
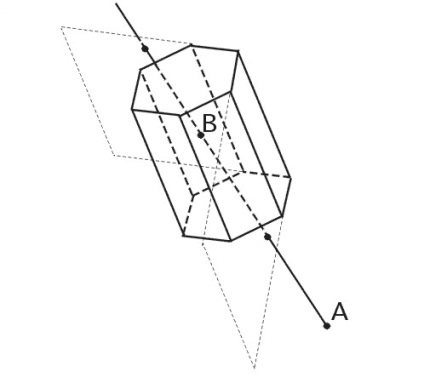
Ábra. 38. Az AB vonal metszéspontjai a prizma arcának síkjával.
Hagyja, hogy a megfigyelő az A ponton legyen. Válassza a B. pontot. amelyről ismert, hogy belső egy konvex alakra, ebben az esetben egy prizmára. Olyan arcot választunk, amelyről tudni akarjuk, hogy látható az A pontból. vagy nem látható. Megépítjük azt a síkot, amelyben a kiválasztott arc fekszik. Megtaláljuk a sík metszéspontját és az egyenes vonalat, amelyet az AB szegmens alkot. Ha az egyenes és a sík metszéspontja az AB szegmensben található. akkor arra a következtetésre jutunk, hogy ez az arc látható. Ha a keresztezési pont az AB szegmensen kívül van. akkor az arc nem látható. Abban az esetben, ha a vonal és a sík párhuzamos, feltételezzük, hogy az arc nem látható.