A teoretikusok wiki-cikke

1. Gyűjtsd össze és tanulmányozzák az anyagot.

2. Találjon meg egy csodálatos számot a természetes számokról.

3. Nyissa meg a szabályzatok és tulajdonságok sorszámát.

4. A megállapítások általános elemzése és következtetés levonása.

A vizsgálat eredményei

Egyszerű és összetett számok

A természetes számot egyszerűnek nevezik, ha csak két osztója van: az egyik és ez a szám. A természetes számot összetettnek hívják, ha több mint két osztó van. Az 1-es számnak csak egy osztója van: maga a szám. Ezért nem tekinthető sem vegyületnek, sem elsődlegesnek. Az első tíz olyan prímszám: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Tetszőleges számú vegyület lehet bontani két tényező, amelyek mindegyike nagyobb, mint 1. A prímszám, így nem lehet tényezőként. A termék két prímszám lehet egy egyszerű szám, ha az egyik szám egyenlő 1, a másik pedig egy prímszám. Minden első szám, a nagy 2, furcsa.

Megoldatlan misztérium a prímek

A prímszámok titka a megmaradt számok közötti elosztás: önkényes, minden rend nélkül. A természetes számsorok egyszerű számai a sorozat bizonyos részeiben egyenlőtlenül fordulnak elő, és másokban több van - kevesebb. A matematikusok évek óta igyekeznek megtalálni ezt a rendet, de sikertelenül. És a megrendelés hiánya azt jelenti, hogy a prémium számokat egymás után kell keresni. A kicsi prímszámokat az úgynevezett "Erastofen Sieve" segítségével könnyű megtalálni. A táblázatban minden számot beírunk 100-ra (az 1 nem tartalmazza: ez nem egy elsőszámú szám). Törölje az összes páros számok kivételével 2. Aztán összes szám törléséhez osztható 3, kivéve 3. A számok osztható 4, már törölték, így folytassa az 5, majd a 7. Az összes többi szám (sárga sejtek) - egyszerű.

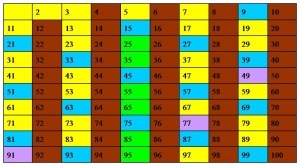
Egyszerű számokat neveznek tégláknak a matematika megépítésében, hiszen az összes többi szám egyszerűen megszorozható. Például 55 = 5 × 11 75 = 3 × 5 × 5 39 = 3 × 13 65 = 5 × 13 221 = 13 × 17 73 939 133 egy elképesztő főszám. Bármelyik számjegyet eltávolíthatja a végéről, és a fennmaradó szám is egyszerű lesz. Ez a legnagyobb ismert szám ebben a tulajdonságban.

Szuper-összetett számok (A könyv "Én ismerem a világot")

Különös, hogy egy személy megtalálja a mindent, amiben foglalkozik, "a Guinness Rekordok Könyve" megerősíti ezt. És melyik szám a legnagyobb? Nincs ilyen szám, mivel minden számot növelhetünk hozzá hozzá. Keressük a bajnokokat a természetes számok között az osztók számával. Az 1-es szám legkevesebb osztója a legkevesebb, csak az egyik az egység. Minden prím esetében két osztó van - maga a szám és az identitás. És melyik természetes szám van a legtöbb elosztóval? Nyilvánvaló, hogy nincs ilyen szám, mivel a természetes szám megszorzásával, mondjuk kettővel, növeljük annak különböző osztóinak számát. A túlméretezett szám olyan természetes szám, amelynek több osztója van, mint minden nagy természetes szám. Melyik szuperszám lesz a legkisebb? Az 1. szám pontosan egy osztó. A 2. és 3. szám pontosan két osztó, mivel egyszerűek. A 4-es szám három osztóval rendelkezik. A 6-os számnak négy osztója van: 1, 2, 3 és 6. Úgy tűnik, hogy a következőnek öt osztóval kell számolnia. A legkevesebb 16, osztó 1, 2, 4, 8 és 16. Ugyanakkor azt meghatároztuk az 12, amely hat alcsoportok: 1, 2, 3, 4, 6, és 12. Ezért, a 16 szám nem válik sverhsostavnym, és ők lettek A következő szám szuperkompozitív lesz a 30 szám nyolc osztóval. Ezután, 36, 40, 54, 56, mind a nyolc elválasztó 48 tíz osztója, száma 60 tizenkét osztója, és csak a 64 szám csak hét alcsoportokat, és így a 36. számú, 40, 48, 54, 56 és 60 svehsostavnymi számok . Kölcsönösen elsőszámú számok

A természetes számok viszonylag elsődlegesek, ha a legnagyobb közös osztójuk 1.

Az első tíz főszámban az ilyen párok 3, 5, 5, 7, 11 és 13, 17 és 19. Az "ikrek" problémája az egyik olyan probléma, amelyet eddig nem sikerült megoldani. Nem ismert, hogy ez a lista valaha is megtörik-e vagy végtelen-e, mint számos prímszám. Barátságos számok

A természetes számot jónak nevezzük, ha azt a számjegyek összegével osztjuk el. A jó számok meghatározásával az 1-9-es számok jó számok. A legkisebb kétszámjegyű szám 10, mivel osztva egy számmal egyenlő (1 + 0). A következő szám 12, mert A 12-et 1 + 2-vel osztjuk meg, amint már bizonyítottuk, ugyanaz a szám szuperkompozit. 13 nem jó szám, mivel a 13 nem osztható (1 + 3); A 14 nem jó szám, mivel a 14 nem osztható (1 + 4); 15 nem jó szám, mivel a 15 nem osztható (1 + 5); 16 nem jó szám, hiszen a 16 nem osztható (1 + 6); 17 nem jó szám, mivel a 17 nem osztható (1 + 7); 18 jó szám, mert A 18. ábra (1 + 8); 19 nem jó szám, mert A 19 nem osztható (1 + 9); Jó számok: 10, 12, 18, 20, 21, 24, 27, 30, 36, 40, 42, 45, 48, 50, 54 stb. Mint látjuk, minden jó szám összetett szám.

A tökéletes szám természetes szám, amely megegyezik a szám osztóinak összegével, kisebb, mint a szám. Pythagoras (VI. Kr.) És tanítványai tanulmányozták a számok felosztásának kérdését. Egy szám, amely megegyezik az összes osztójának összegével (a szám nélkül), a tökéletes számot hívták. Például egy 6 = 1 + 2 + 3, ahol az 1, 2 és 3 egy osztója 6. 28 = 1+ 2 + 4 + 7 +14, ahol a számok 1, 2, 4, 7 és 14 osztói 28. A következő elkötelezett száma - 496 = 1+ 2 +4 + 8 + 16 + 31 + 62 + 124 + 248, ahol a számok 1, 2, 4, 8, 16, 31, 62, 124 és 248 osztói 496 pythagoreusok ismerte csak az első három tökéletes szám. A negyedik tökéletes szám - 8128 vált ismertté az 1. században. Az ötödik - 33550336-ot a 15. században találták meg. Tökéletes számok szorosan kapcsolódnak a Mersenne prímszámok, azaz számok formájában 2m - 1. Még Euclid találtuk, hogy a szám n = 2m-1 (2m - 1) tökéletes, ha 2m - 1 prím. 1983-ra már 27 tökéletes szám volt, és az összes talált tökéletes szám páros szám. Az első 23 ilyen számok megfelelnek az m értékek: 2,3,5, 7, 7,13,17,19,31,61, 89,107,127,521,607,1279,2203,2281,3271,4219,4423,9689,9941,11213. De eddig a tudósok nem tudják, hogy vannak-e páratlan tökéletes számok, ott van a legnagyobb tökéletes szám.

A háromszög alakú számok Pythagoras (ie I. század) és tanítványai a geometriai alakzatokhoz kapcsolódó szekvenciákat tekintettek. Megszámoljuk a körök háromszögek, négyzetek, ötszög kaptak: - a szekvencia (a2) a háromszög alakú számok 1, 3, 6, 10, 15, ... a következőképpen állítjuk elő: 1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4, 1 + 2 + 3 + 4 + 5, ..., az 1, 4, 9, 16, 25, ..., négyzetek sorrendje (b2). a következőképpen állítjuk elő: 1, 1 + 3, 1 + 3 + 5 1 + 3 + 5 + 7, 1 + 3 + 5 + 7 + 9, ..., n 2 - szekvencia (c2) ötszögletű szám 1, 5, 12 , 22, 35, ... így kapható: 1, 1 + 4, 1 + 4 + 7, 1 + 4 + 7 + 10.4 + 7 + 10 + 13, ...,

Nugget számok Vegyük a számokat 5, 10, 11, 13, 17, 25, .... Minden számot, kivéve az 5-et, egyetlen szabály alkotja. A számjegyek száma hozzáadódik a számhoz. Tehát 5 + 5 = 10, 10 + 1 = 11, 11 + 2 = 13, 13 + 4 = 17, ... Minden az 5-ös számmal kezdődik. Egyértékű csomók egyszerre találhatók 1, 3, 5, 7 és 9. A kétjegyűek közül a legkisebb a 20, aztán a 31, ... A többszámú számok között van egy "nuggets" gyűjtemény. Például 132, 143, 233, 929, 1952 stb.

A számot hívják szimmetrikus, ha van egy vonal (vagy közepén szimmetria), hogy hordozza azt a számot önmagával. Ha figyelembe vesszük mind a tíz szám: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, ez látható: csak a 8. ábrán van egy függőleges szimmetriatengelye l és szimmetrikus szám képest ez a függőleges tengely (A vonal). Digitális 0 két szimmetriatengelye, függőleges és vízszintes, és az egyik központja szimmetria (a központ - a metszéspontja a függőleges és vízszintes tengelyek a szimmetria).

A 8-as és 0-as számok szimmetrikusak, tehát minden szimmetrikus szám ezekből a számjegyekből áll. A legkisebb és az egyetlen két számjegyű szám a 88-as szám. A 88-as szám szimmetriatengelye az a vonal, amely az első nyolc és a második közé esik. A következő szimmetrikus szám a 808-as szám, amelynek függőleges szimmetriatengelye p, a második szimmetrikus háromjegyű szám a 888-as szám.

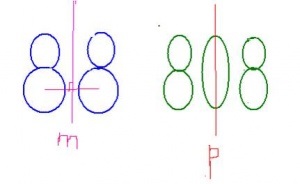
Négyjegyű szimmetrikus számok: 8008, 8888. Ötjegyű szimmetrikus számok: 80008, 80808, 88088, 88888.

A számok körülveszik minket és segítenek minket mindenben a dolgainkban. Ezek a számlák eszközei. Számok nélkül nem tudnánk, mi a mai nap, és milyen idő alatt. Manapság számok vannak mindenütt, és mindig szükségünk van rájuk. Nehéz elképzelni, hogy mi lesz a világ, ha nincs számunk! A szám a matematika alapfogalma, amely hosszú történelmi fejlődés során alakult ki. A szám koncepciója szoros kapcsolatban áll a mennyiségek tanulmányozásával; ez a kapcsolat most megmarad. A modern matematika minden területén figyelembe kell venni a különböző mennyiségeket és a számok felhasználását. A tárgyak kiszámításának szükségessége a természetes szám fogalmának megjelenéséhez vezetett. Minden nép, aki írott nyelven volt, rendelkezett egy természetes szám fogalmával. A "szám" fogalmának sok definíciója van. A szám első tudományos meghatározását Euklid "kezdeteiben" adta: "Az egység az, amely szerint minden meglévő dolog az egyik. A szám egy egység. " Korábban Euklid Arisztotelész adta ezt a definíciót: "A szám egy olyan egység, amelyet az egységek segítségével mérünk." Még Miletus Thales is - a görög spontán materialista filozófia alapítója - azt tanította, hogy "a szám az egységek rendszere". Az ókori görög matematikus Pythagoras azt mondta ezen: „A szám a törvény és a kötés a béke uralkodik az istenek és halandók”, „A dolgok lényegét az a szám, amely lehetőséget nyújt mindent egy egység és a harmónia”, „Minden szám.” Annak „általános aritmetikai” (1707), a nagy angol fizikus, mérnök, csillagász és matematikus Sir Isaac Newton írta: „A szám azt jelenti, nem annyira egy sor egységek elvont viszony valamilyen mennyiséget egy másik mennyiséget ugyanolyan vett egységnyi . A szám háromféle: egész, tört és irracionális. Egy egész szám egy egység által mért érték; frakcionális - egy egység többszöröse, irracionális - olyan szám, amely nem egyezik az egységgel. " Nincs vége a természetes számok csodálatos tulajdonságainak tanulmányozásához. Csoportunk számos természetes számot tanulmányozott érdekes funkciókkal, egyszerű és összetett számokkal, szuperszámítógépes számokkal, tökéletes számokkal és jó számokkal, két számmal, barátságos számokkal, egyszemélyes számokkal, szimmetrikus számokkal. A téma tanulmányozása során alaposan tanulmányozhatta az iskolai tantárgyakat, az egyszerű és összetett számokat. Megismerkedtünk a speciális kétjegyű számokkal, amelyekben a kétjegyű számok terméke nem változtatja meg értékét, ha átrendezzük számainkat. A csodálatos számok szimmetrikus számok. Számos természetes számot tanulmányozva sok természetes számok szingularitása található. Általában a feladatok megvalósultak. Az ókori görög matematikus Euklid (Kr. E. III. Század) "Elements" című könyvében, amely kétezer évig a matematika alapvető tankönyve volt, bebizonyította, hogy végtelen sok prím van, minden prímszám esetében még nagyobb elsőszámú szám van. Hipotézisünk helyes volt, a legnagyobb prímszámot, a vegyületet, a tökéletes, a szimmetrikus értéket feltüntetni lehetetlen. A téma tanulmányozása során alaposan áttanulmányozták az iskolai tantárgyakat, egyszerű és összetett számokat. A szuperszámítógépes számok megismerése érdekében, a kettős számjegyű számok, azaz a kétjegyű számok terméke nem változtatja meg értékét, ha átrendezik számukat. Új a csodálatos számokhoz - ezek jó és szimmetrikus számok, a számok csomók. Itt megáll a természetes vonalon. Nem sok figyelmet fordítanak a matematika kezdeti lépéseire? Erre válasz lehet a német matematikus Leopold Kronecker (1823-1891): "Isten természetes számokat hozott létre, minden más az emberi kéz munkája".

Hasznos források

• www.mersenne.org

• Bosova LL Informatika: a hatodik osztály tankönyve, az "Anyagi kíváncsi anyag"

• Algebra 9. fokozat ed. Makarycheva MN .. Glazer GI "A matematika története az iskolában", M: Felvilágosodás, 1982.

Egy könyv a diákoknak "Értem a világot"

• "Matematikai Encyclopaedia" / Ch. Ed. IM Vinogradov.-M .: Soviet Encyclopedia

• Textbook matematika 6. osztály besorolása: N. Ya. Vilenkin

Egyéb dokumentumok