A minimális átlagos négyzetes hiba számításai

Az automatikus vezérlőrendszerek elmélete

Ha az automatikus rendszert egyidejűleg hasznos jelzéssel és interferenciával üzemeltetik, akkor a probléma a rendszer optimális számításából adódik, hogy a legkisebb hibát eredményezze. A hasznos jel legjobb reprodukálása szempontjából a rendszernek a lehető legnagyobb sávszélességnek kell lennie, és az interferencia legjobb elnyomásának szempontjából a rendszernek éppen annyira sávszélességgel kell rendelkeznie. Itt az optimális megoldás megszerzésének kritériuma az eredményes rendszerhiba minimális értéke, amelyet a hasznos jel és interferencia határoz meg.

Véletlenszerű változók esetén a legegyszerűbb a gyökér-négyzethármas hiba meghatározása, ezért az automatikus rendszer pontosságának becslésére használják.

Tekintsük a rendszer kiszámítását a minimális átlagos négyzetes hiba kritériumán alapulva, egy hasznos jel és interferencia egyidejű működésével.

E kritérium szerint a hiba nemkívánatossága arányos a nagyságának négyzetével. Egy ilyen kijelentés gyakran logikus, de persze nem lehet teljes egyetemességre való jogosultság. Bizonyos esetekben például bármilyen célra történő felvétel során minden hiba nagyobb, mint egy bizonyos érték, egyáltalán nem kívánatos. Azonban az ellenőrzési rendszer átlagos négyzetes hibája

szinte minden esetben a legegyszerűbb számított érték, amely meghatározta ennek a kritériumnak a használatát.

A probléma számos megfogalmazása lehetséges. A legegyszerűbb probléma a következőképpen fogalmazható meg. Ha van valamilyen rendszer egy adott struktúra automatikus vezérléséhez, akkor a rendszer paramétereit ki kell választani annak érdekében, hogy a hasznos jel és interferencia adott statisztikai jellemzőihez minimálisan gyökér-négyzetes átlag hibát kapjunk.

Ez a probléma a következőképpen oldható meg. A hiba spektrális sűrűségével integrációjával megoszlik a diszperzió. A diszperziót a hasznos jel, interferencia és rendszerparaméterek valószínűségi jellemzőitől függően kapjuk meg. Ezt követõen olyan feltételeket kell keresni, amelyeknek a rendszer paramétereihez kell kapcsolódniuk a különbség minimális elérése érdekében. A variancia viszonylag egyszerű kifejezésével ez határozható meg a differenciálódás és a részleges származékok nullára történő egyenlítése révén.

Bonyolultabb esetekben meg kell keresni a minimális varianciát az érdeklődési paraméterek numerikus beállításával és a megfelelő grafikonok szerkesztésével, valamint a számítógép kiszámításával.

valamilyen transzformációs képlet segítségével

- a differenciálódás problémája, H

- statisztikai előrejelzés (előrejelzés), és így tovább.

A rendszer fenti hibája a formában megjeleníthető

A zárt rendszer súlyfüggvénye.

A (11.130) és (11.131) helyettesitését a (11.129) képletbe állítjuk elő

A probléma az, hogy megtaláljuk a Fourier-transzformációhoz tartozó súlyfüggvényhez tartozó zárt rendszer frekvenciaátviteli funkcióját

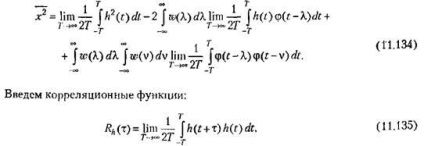
A zárójeleket (11.132) nyitjuk meg, és megváltoztatjuk az integráció sorrendjét:

Ennek eredményeképpen a kifejezés (11.134) átformálható a formára

akkor az integráció alsó határait (11.138) nulla értékre kell állítani. Ennek eredményeképpen kapunk

Az utolsó kifejezés azt mutatja, hogy a hiba átlag négyzetének megfelelő optimális súlyfüggvényt csak a hasznos jel és interferencia korrelációs függvényei határozzák meg.

Megmutatható [88], hogy a súlyfüggvényre kiszámítható kifejezés (11.139) minimalizálásához szükséges és elégséges feltétel az, hogy a Wiener-Hopf integrált egyenlet megoldása

Az optimális tömegfunkciónak megfelelő optimális átviteli függvény (11.133), amely a (11.140) egyenlet megoldása,

azaz az úgynevezett optimális simítás esetén van

Ebben az esetben a megoldás (11.1-11) egyszerűen ábrázolható:

Ennek a kifejezésnek a számlálója a következőképpen van meghatározva. Vegye figyelembe a következő kifejezést:

-

Amikor az optimális átviteli függvényt a rendszerben realizáljuk, az átlag négyzetes hiba elméleti minimális értékét kapjuk. Ezt a minimális értéket a

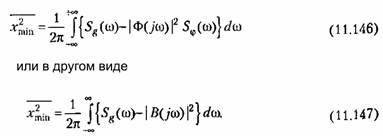
Tekintsünk példát példázatra. Tegyük fel, hogy egy hasznos jel u

a rendszer bemenetére való interferencia megfelel a spektrális sűrűségnek:

Iaidm a spektrális sűrűséget (11.136):

Az első kifejezés zárójelben történő elvetése az alsó fél síkban lévő pólusnak megfelelően megtaláljuk az előírt átviteli függvény számlálóját (11.143):

Az optimális átviteli funkció megtalálása nem jelenti azt, hogy az igazi automatikus rendszer optimálisan működhet, mivel megvalósítása nagy nehézségekkel járhat. Az optimális átviteli funkciót - a legegyszerűbb esetek kivételével - ideális funkciónak kell tekinteni, amelyhez azonban valódi automatikus rendszer teljesítményére kell törekedni. Az optimális rendszerek elmélete [22, 88, 89].