A frakciók csökkentése és "kiterjesztése"
A frakció nagysága nem változik, ha a frakció számlálóját és nevezőjét ugyanazon a számmal szorozzák.
= =;
= =;
= =;
Egy ilyen frakció ilyen átalakulását egy frakció "kiterjesztésének" nevezik. A frakciót a frakcióból a 6-ra növeljük.
A frakció mérete nem változik, ha a számláló és a frakció nevezője azonos számmal van felosztva.
Az ilyen átalakulást egy töredék összehúzódásának nevezzük.
A "százalék" szó a latin "procento" -ból származik, ami "százról" szól.
A százalék a szám századrésze,% -kal jelezve.
Bármely egész szám (például 1) 100%. Század része 1. 100 = 0,01. Ezért az egység 1% -a 0,01 lesz.
Ha a probléma az egész érték ismeretlen, és csak részei ismertek, akkor feltételezzük, hogy 100% vagy 1 (egy). Ha az egész valamilyen részből áll, akkor ezek a részek frakciók, amelyek összege egyenlő az egésznek (1). Ezeknek a frakcióknak arányos része az egésznek része lehet százalékban.
Ha a teljes térfogat 100%, akkor minden egyes rész (minden egyes frakció) nagyobb, mint 0%, de kevesebb, mint 100%, és az összes részösszeg százaléka 100%. Valamely érték százalékos értéke ennek az értéknek a hányadosa, tehát ha 1 = 100%, akkor minden egyes frakció (rendes vagy tizedes) megegyezik egy százalékos százalékkal.
Példa: Keresse fel az ezredik 0,3442524 számot.
Ezer a vessző után a harmadik számjegy, ami azt jelenti, hogy meg kell vizsgálnunk a negyedik számjegyet:
0,3442 524 - ebben az esetben 2, tehát kerekítünk és 0,344-et kapunk.
Emlékezzünk arra, hogy a 0,1,2,3,4 ábrák lefelé kerekítve. Az 5,6,7,8,9 ábrákon kerekítettek. Így van öt esetünk, és kerekítéssel a kisebb és nagyobb oldalra.
Szöveges feladatok # 8213; ez az egyik legkedveltebb feladat, különösen a középiskolások számára, mert minél tovább bonyolítja az állapotot, annál nehezebb lesz egy egyenlet létrehozása és a probléma helyes megoldása. De mint a matematika bármely témájában, ahhoz, hogy bizakodóan megoldja a komplex problémákat, meg kell oldania a legalapvetőbb technikákat.
Ezeket a problémákat a kezdetektől fogjuk elemezni. A szöveges probléma abból áll, hogy egy adott helyzetet leírtunk, és azt a kérdést, hogy melyikre kell választ adni.
Példa: A Kolya 5 matricával ragasztott 2 matricát. Hány matricát tapasztalt Kolya?
Állapot: Kolya ragasztott 5 db 2 matricával.
Kérdés: Hány matricát tapasztalt Kolya?
A szöveges probléma megoldása több fő szakaszra bontható:
· Az állapotfeltárás;
· Számos különböző feltétel létezhet egy egyenletre.
1. feltétel: Masha és Petya együtt talált 5 gomba. Masha talált 2. Hány gomba találta meg Petya?
2. feltétel: A csokor kamilla és harangokból áll. Összesen 5 virág van a csokorban, 2 közülük kamilla. Hány harang van a csokorban?
3. feltétel: 5 fa játék volt a fán. Két közülük esett, és összeomlott. Hány játék marad a fán?
A munka megkönnyítése érdekében hasznos az illusztráció vagy a modellezés használata. Ez lehet a feltétel rövid, matematikailag vagy verbális megfogalmazása. Ez egy további rajz vagy táblázat is lehet.
Példa: Petya magasabb, mint Koli, Seryozha Kolya alatt van. Ki magasabb?
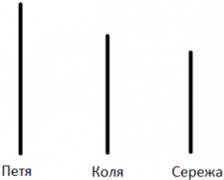
A képről egyszerre a válasz egyértelmű: Petya mindenek felett van.
Ahhoz, hogy az egyenletet a probléma állapota alapján dolgozzuk fel, különböző módszereket alkalmazunk, attól függően, hogy a mennyiségi függőség állapotában megadjuk-e.
Ezt a függést szavakban fejezzük ki: magasabb / alacsonyabb, több / kevesebb, drágább / olcsóbb, hosszabb / rövidebb stb.
Az egyenlet megfogalmazásában a "be" és az "on" előpozíciók különleges jelentőséggel bírnak.
Példa: Petya 20 cm feletti Kolja felett, Serezha 10 cm alatt Kolja alatt van, hány cm Petya magasabb, mint Seryozha?
Megoldás: Legyen Π # 8213; növekedés Petit, K # 8213; a Koli, C # 8213; Seryozha növekedése.
By the way, figyeljen erre a módszerre # 8213; válaszd a "beszélő" változókat, és ne az arc nélküli X és Yi játékokat, nehogy zavarodj az egyenlethez.
A fiúk növekedését fejezzük ki.
A Petya 20 cm fölött van Koli fölött: P - 20 = K.
Serezha Kolya alatt 10 cm-nél: K = C + 10.
A Koli növekedését az első egyenletben helyettesítettük: П-20 = С + 10.
Meg kell találnunk, milyen messze van Petya a Seryozha felett: P - S.
Megkapjuk, hogy Petya 30 cm-rel magasabb, mint Seryozha.
Példa: A munka leckében a diákok hópelyheket készítettek. Összesen 12 hópelyhet készítettek. Masha kétszer annyi hófehérjét csinálta, mint Kolé. Kolya kevesebb 4 hópelymet készített, mint a romák. Hány hópelyhet csinált Masha?
Tegyük fel, hogy M # 8213; a Masha által készített hópelyhek száma, K - Koli hófehérje, R # 8213; hópelyhek Roma.
Masha kétszer annyi hópelymet készített, mint Kolé: K = M / 2.
Kolya 4 hópelyheket hozott kevesebb, mint a romák: P = K + 4 = M / 2 + 4.
A srácok együtt 12 hófehérjét készítettek: M + K + P = 12.
Az M: M + M / 2 + M / 2 + 4 = 12 értékekkel helyettesítjük az összes értéket.
Masha 4 hópelyhet készített.
százalékában # 8213; ez mindig töredéke egy számnak.
100% # 8213; az összes szám;
50% # 8213; fele;
25% # 8213; negyedévben.
Ha 1% -ot keres, akkor 100-ra kell osztania az egész számot.
Az almák 1% -a # 8213; = 1 alma.
Az összes körte 1% -a # 8213; = 2 körte.
A százalékok feldolgozásához az arányt alkalmazzuk, amelyben a valós értékek egy oszlopban íródnak, egy másikban # 8213; megfelelő kamatot.
200 körte # 8213; 100%;
A fejlődés a mennyiségek függőségét tükrözi. Más módon két frakció formájában lehet leírni: =.
A frakciókkal való munkavégzés szabályain alapulva az alábbiak szerint dolgozhatunk:
· Az értékeket egyetlen frakcióban csökkentheti.
· A keresztértékek terméke 200 # 8729; 1 = 2 # 8729; 100.
Ezt a témát részletesen tárgyalja a tanfolyam.
Továbbá a szöveges feladatok a progresszióhoz, a termelékenységhez, a tempóhoz kapcsolódnak # 8213; erről mindannyian beszélünk a tanfolyamon. Most pedig kezdjék el a képzési feladatokat.
trapéz # 8213; Ez egy négyszög, amelynek két ellentétes oldala párhuzamos.
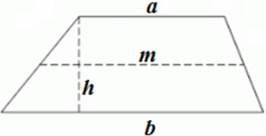
h # 8213; a trapéz magassága (a bázisok közötti távolság);
m # 8213; a trapéz középvonala (a trapéz oldalirányú oldalait összekötő szegmens).
A trapéz középvonala egyenlő a bázisok összegének felével: m = és ezzel párhuzamosan:
1) Négyszögletű # 8213; Trapéz, amelynek oldalirányú derékszöge van:
Az oldal a magasság.
2) Az ócsuklós # 8213; trapéz, amelyben az oldalak egyenlőek:
· A bázisok szöge egyenlő
· Az átló hosszai megegyeznek
A trapéz (és bármelyik négyszög) belső szögeinek összege 360 °.
· A szomszédos szögek összege 180 °.
· A trapéz alakja egy körbe írható, ha a trapéz alapjainak összege megegyezik az oldalsó oldalak összegével.
· Ha a trapéz körbe írható, akkor a trapéz alakú # 8213; egyenlő szárú.
· Az izzűrű trapéz alakról egy kör leírható.
S = m # 8729; h. ahol m # 8213; középső trapéz vonal.