Solenoid vektor mező
A vektor mezőt szolenoidnak nevezzük. ha létezik ilyen vektor mező. amelynél a mező a rotor mező :.
Egy mezőt vektor mezõ vektorpotenciálának nevezünk.
A vektor mezõ mágnesszelepjének jele: a vektor mezõ solenoid, ha és csak akkor, ha divergenciája nulla. (14)
A WPW hozzávetőleges változatának meghozatala
Probléma 1. Számítsuk ki a munkaerő mozgás közben a pont az erő alkalmazása mentén egy előre meghatározott görbe pont L. B. pont C. Ha a paraméter értékét t a B és C pontok vannak megadva :.
A munka kiszámításához a második típus görbületi integrálját (formula (3)) használjuk:
A lecsökkentett görbületi integrál egy meghatározott integrálra van redukálva a BC görbe paraméteres egyenleteivel:
Egy adott görbe esetén:
Így a munka megtalálásához egy meghatározott integrálszámot kell kiszámítanunk:
A változó változását egy meghatározott integrálissá tesszük:
Az "integráns egy részének összegzését a különbség jele alá" összegezve használjuk:
A: U. munkát.
2. feladat: A mozgó pont sugárvektorja meg van adva:
. A mozgás kezdete után 2 percen belül találja meg a pont sebességének és gyorsulásának vektorát.
A vektorfüggvény koordinátarendszerben van megadva:.
Megtaláljuk az x (t), y (t) z (t) vetületének első és második deriváltjait a t argumentumra vonatkozóan:
Találjuk meg a pont mozgásának sebességét és gyorsulását a (4) és (5) képletek szerint:
A mozgás kezdete után 2 percen belül a sebesség és a gyorsulás vektorok:
3. feladat: Adott egy vektor mezőt és a d sík egyenletét. 3x + y + 2z - 3 = 0. Szükséges:
1) megtalálják az áramlási mező révén a háromszög síkjában ABC ahol AV és C - metszéspontja a sík a koordináta-tengelyek d, merőleges irányban sík orientált „a származási”; készítsen egy tervet az OABC piramisról. ahol D a származás;
2) az Ostrogradsky-Gauss-formula felhasználásával számítsuk ki a mező áramlását az OABC-piramis teljes felületén a külső normál irányában.
1) A mező fluxusának kiszámításához az ABC háromszög síkjánál a (6) képletet használjuk: SAWS =. ahol D az ABC háromszög vetülete az xOy síkra. F egy függvény, amely meghatározza a d-síkot. amely az ABC háromszöghez tartozik.
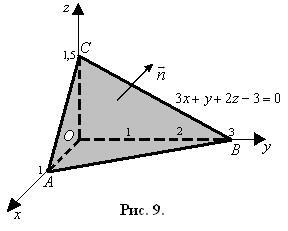
Construct piramis rajz, üzembe a koordinátatengelyeken A. B. C, és csatlakozott hozzájuk az elején koordináták O (ábra. 9).
A sík egyenletéből d. 3x + y + 2z - 3 = 0, melynek formája F (x, y, z) = 0.
Mivel a gradiens mindhárom előrejelzése pozitív, ez a vektor éles szögeket képez a koordináta tengelyeivel, azaz. a "d származtól" irányítják a d síkhoz képest. Ez azt jelenti, hogy a vektor és az egységvektor a "külső" normális. meghatározott a probléma, azonos irányban, így a számítás az átfolyást a a háromszög síkjában ABC csökken egy számítást a kettős integrál: Paws = + (mielőtt a szerves beállított a „+” jel), ahol AOV - vetülete a ABC háromszög XOY síkban.
Az AOB háromszög mentén az integrációs határértékek meghatározása (10. ábra) az AB egyenes egyenletét az xOy síkban találjuk:
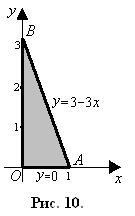
Így a mező áramlása az ABC háromszög síkján keresztül:
A belsõ integrált értéket az y változónál számoljuk ki:
A külső integrált értéket az x változó tekintetében számoljuk ki:
2) A mező fluxusának kiszámításához az OABC piramis teljes felületén. használjuk az Ostrogradsky-Gauss képletet:
Találjuk meg ennek a mezőnek a divergenciáját a (8) képlet segítségével :. A mezőhöz kapunk:
A mező áramlását az OABC piramis teljes felületén számoljuk ki:
. hol van az OABC piramis mennyisége? Ez a kötet a következőképpen számítható ki:
Ennek eredményeképpen:.
Probléma 4. Ellenőrizze, hogy a vektor erőtere potenciál vagy szolenoid. Abban az esetben, mező megtalálja a lehetségesség és a kapacitás felhasználásával számítható épület munkaerő Amikor az egységet súlya az M pont (0,1,0), hogy egy pont n (1,2,3).
Egy vektor mezõ potenciáljának ellenõrzéséhez a rotort a (10) képlet alapján találjuk:
Ezért a mező potenciálisan.
A terepi solenoiditás ellenőrzéséhez a (8) képlet alapján találjuk a divergenciát:
Következésképpen a mező nem solenoid.
Ahhoz, hogy megtalálják a potenciális U (x, y, z) vektor mező Vegyünk egy fix pont (0,0,0), az aktuális C pont (x, y, z) és kiszámítja a vonalintegrál mentén törött VEKC. amelynek kapcsolata párhuzamos a koordináta tengelyével és E (x, 0,0), K (x, y, 0) (lásd a 7. ábrát). A (12) képlet segítségével megkapjuk a következőket:
Elértük a mező potenciálját. ahol C egy tetszőleges konstans. A megoldás ellenőrzéséhez megtaláljuk a lehetséges gradienseket. . Következésképpen az erõteret potenciálját helyesen találjuk meg.
Lássuk egy vektormezõ munkáját, amikor az M (0,1,0) ponttól az N (-1,2,3) pontig egy (11) képletû egység tömegét mozgatjuk:
Válaszok: a mező potenciálisan nem solenoid; . ahol C jelentése tetszőleges konstans; munka A = -10.