Interpoláció az aitken sémán keresztül - matematika

2. Interpoláció az Aitken rendszer szerint

Az interpolációs Iteratív módszerek néhány egyszerű interpolációs séma ismételt alkalmazásán alapulnak. Az iteratív módszerek közül a leghíresebb az Aitken-módszer, amely a lineáris interpoláció többszörös alkalmazásán alapul.

Reakcióvázlat szerint Aitken lineáris interpolációval pontok Mi (XI. Yi) és Mi + 1 (xi + 1 Yi + 1) csökkenti a számítás a meghatározója a másodrendű

Ha három vagy több pontot interpolál, a polinomokat

Általános esetben az n-edik fokú interpolációs polinom, amely az yi (i =) értékeket veszi figyelembe az xi pontokban, az alábbiak szerint írható:

A fő előnye az a lehetőség, Aitken rendszer fokozatos növekedése az értékek xi alkalmazhatunk mindaddig, amíg az egymást követő értékek P0,1,2, ..., n (x) és a P1,2, ..., n-1 (x) nem egyezik egy előre meghatározott pontossági . Más szavakkal, a számítások leállnak, amikor a feltétel

Amikor a számítógép számítási a (3) képlet vannak megvalósítva rekurzív szubrutinok - funkció PX (I, J) a formális paraméterek I, J, meghatározó kódok extrém interpolációs csomópontot, amelyeket használni ahhoz, hogy megfelelő érték polinom Pi, i + 1, ..., j (x).

A P (x) kiszámított értékeinek tárolásához egy N * N méretű M méretű kétdimenziós tömböt használunk, ahol N az interpolációs csomópontok maximális száma. A P (x) minden lehetséges értéke megegyezik az M (I, J) elemek egyikével, a fõ átló felett (I

Például, az érték P1,2 (x) polinomot megfelelő elem M (1,2), az értéket P2,3,4 (x) - M elem (2, 4) stb Szimmetrikus elemek M (J, I), elhelyezett alatt a fő diagonális (J> I), jelzi, hogy a megfelelő értékek a P (x) ebben az időben kiszámítani, és meghatározott, mint

A PX rekurzív eljárás sémáját az 1. ábrán mutatjuk be. 1, ahol X az interpolációs csomópontok egy tömbje, Y a függvényértékek tömbje az interpolációs pontokon, és Z az argumentum értéke. Az X, Y, Z, M paramétereket a főprogram és a PX-rutin közös jellemzőinek kell tekinteni.

3. Newton interpolációs formulái az egyenlő távolságra lévő csomópontokhoz

Interpoláció csomópontok x0. x1. xn nevezzük ekvidisztáns, amikor, ahol h - lépése interpolációval. Sőt, néhány függvény f (x) értékeket táblázatos alakban a yi = f (xi), ahol xi = x0 + IH.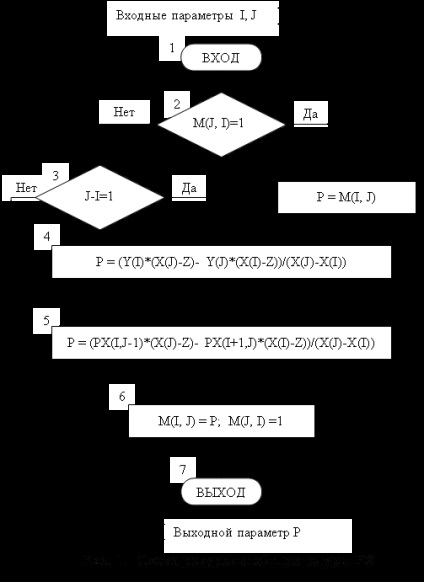

Két Newton-képlet létezik az egyenlő távolságú interpolációs csomópontok esetében, amelyeket Newton első és második interpolációs képletének neveznek, és amelynek formája:

;

,

Ezekben a képletekben D i yj véges különbségek, ahol i a különbség sorrendje, j a sorozatszám, és a t és q paraméterek a következők szerint vannak meghatározva:

Az első rend véges különbségeit Dyj = yj + 1-yj-ként számítjuk ki. ahol

j =, a magasabb rendeknél az ismert formula

Az így létrejött véges különbségeket célszerűen táblázatos formában ábrázolják, például táblázatok formájában. 1, melyet véges különbségek horizontális táblázataként neveznek.

A Newton első képletét az interpoláció előrehaladására használjuk, és visszamenőleg extrapoláljuk. a különbözet ​​táblázat elején, ahol a sorok kitöltődnek és elegendő számú véges különbség van. Ennek az interpolációs képletnek az alkalmazásával az x argumentum értékének a [x0. x1]. Ezenkívül x0 esetén az xk interpolációs pont indexel, ahol m a véges különbségek maximális sorrendje.

A második Newton-formulát az interpolációra alkalmazzuk hátrafelé és előre extrapoláljuk, azaz. a véges különbségek táblázatának végén. Ebben az esetben az x argumentum értékének az [xn-1] intervallumban kell lennie. xn], és minden interpolációs csomópont xn-ként vehetõ.

A véges különbségek egyik legfontosabb tulajdonsága a következő. Ha az i. Sorrend véges különbségei (pl

ahol L a számértékek száma a vessző után a függvény értékeinek ábrázolásakor.

Meg kell jegyezni, hogy Newton képletek a Lagrange-képlet módosításai. Azonban, Lagrange képlet nem lehet elhanyagolni bármelyik feltételeket, mivel ezek mind egyenlő és polinomok n-ed-fokú. A Newton-képletek közé tartoznak a növekvő fokú polinomok, mint koefficiensek, amelyek koefficiensei a véges különbségek és a faktorok. Véges különbség általában rohamosan, így szempontjából elhanyagolható Newton képletek, amelynek együtthatói lesz kicsi. Ez biztosítja, hogy a funkció közbenső értékeit egyszerű interpolációs képletekkel kellő pontossággal kell kiszámítani.

Információ a munkáról "A funkciók interpolációja"