A szorzás és kiegészítés szabályai
Látjuk, hogy bár az 1. és 2. példák nagyon eltérőek, megoldásuk pontosan ugyanaz. Ezek a szaporítás általános szabályán alapulnak.
Annak érdekében, hogy megtaláljuk az A és B tesztek független elvégzésének minden lehetséges eredményét, szorozzuk meg az összes A vizsgálati eredmény számát és a B. összes vizsgálati eredmény számát.
A két független tesztre vonatkozó szorzási szabályt egyszerűen téglalapok segítségével osztják négyzetekre vagy téglalap alakú táblákra. De ha három teszt van, akkor illusztrációként a hosszúságot, a szélességet és a magasságot kell használni, és a képen egy négyszögletes párhuzamos lesz, kockákra osztva. Itt a rajzok és a magyarázatok nehezebbek lesznek, mert például láthatatlan kockák lesznek. A helyzet még rosszabb a négy tesztnél. Ebben az esetben a képhez egyszerűen nincs elég mérés, mert a környező tér teljesen háromdimenziós.
Kiderül, hogy a három, négy, stb. Próbákra vonatkozó szaporítási szabály magyarázható anélkül, hogy túlmennené a síkot, egy geometrikus modell segítségével, amelyet az esetleges változatok faaként neveznek. Először is, mint bármely kép, és másodsorban lehetővé teszi, hogy mindent figyelembe vegye, anélkül, hogy hiányolna valami.
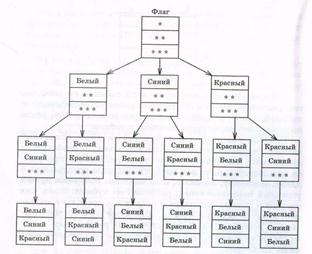
A megoldás. A megoldást a lehetséges variánsok fa segítségével keresjük (lásd a 4.1. Ábrát). Nézzük a bal "ágát", ami a '' zászlóból '', hagyja, hogy a felső sáv fehér legyen, akkor a középső sáv legyen kék vagy piros, az alsó pedig piros vagy kék. A zászlócsíkok két színváltozatából kiderült: fehér, kék, piros és fehér, piros, kék.
Tegyük fel, hogy a felső sáv - a szín kékje - a második "ág".
Ezután a középső sávnak fehérnek vagy pirosnak kell lennie, az alsó pedig vörös vagy fehér. Kiderült még két változata a színeknek a színek: kék, fehér, vörös és kék, piros, fehér.
Hasonlóképpen figyelembe veszik a vörös szín felső sávjának esetét is. Még két lehetőség van: piros, fehér, kék és piros, kék, fehér zászlócsíkok. Csak 6 kombináció.
Az elkészített séma tényleg olyan, mint egy fa, csak fejjel lefelé. Nyilvánvalóan ezzel összefüggésben azt is nevezik a lehetséges variánsok faaként.
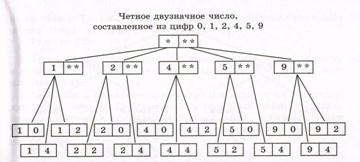
Így például az 1. példa (4.2. Ábra) lehetséges változatainak fája van:
4. példa Három izzólámpa lóg a folyosón. Hány különböző módja van a folyosó megvilágítására?
Az első út. Számoljuk ki az izzókat, és írjuk a '' + '' vagy '' - '' lépéseket, hogy a következő fény világít-e vagy sem. Az összes világítási mód egyszerűen felsorolható: + + +, + + -, + - +, - + +, + - -, - + -, - - +
Csak 8 módon.
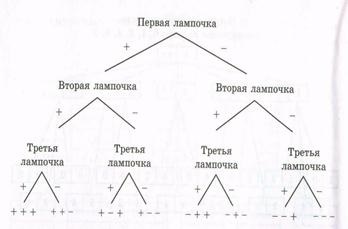
A harmadik út. Az első lámpa be- vagy kikapcsolható, ᴛ.ᴇ. Két lehetséges kimenet van. Ugyanez vonatkozik a második és a harmadik izzókra is. Feltételezzük, hogy az izzók égnek vagy nem függetlenül. tovább
4.3. Ábra: a szorzás szabálya, azt kapjuk, hogy a világítási módok száma 2 ‣ ↓ ↓ ↓ ↓
Mindhárom megoldás közül mindegyiknek megvannak az előnyei és hátrányai. A megoldás választása a tiéd! Megjegyezzük, hogy a szorzási szabály lehetővé teszi számunkra, hogy egy lépésben számos problémát megoldjunk. Például a matematikai tényezõ rendkívül fontos tényezõje. Nézzük először a példákat.
5. példa A család - 6 fő, és az asztalnál a konyhában 6 szék található. A családban úgy döntöttek, minden este, vacsorázva, hogy új módon üljön le a 6 székre. Hány napot lehet a családtagok megismételni?
A megoldás. A válasz meglepően nagy: csaknem két év! Megmagyarázzuk. Az érvelés megkönnyítése érdekében feltételezzük, hogy a család (nagymama, nagyapja, anyja, atyja, lánya, fia) váltakozva ül a székeken. Érdekelünk, hogy hányan vannak különböző módok arra, hogy azokat székre helyezzék.
Tegyük fel, hogy az első telepíti le a nagymamát. Hat lehetősége van a szék kiválasztására. A második nagyapával leül, és önállóan választja meg a többi öt székét. Anya választja a harmadikt, és 4 székekből választhat. A pápának már 3 lehetősége van, a lánya - 2, nos, és a fiú egyetlen üres székre ül. A szorzás szabályával azt találjuk, hogy 6 · 5 · 4 · 3 · 2 · 1 = 720 különböző elhelyezési mód van. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, a "játékban ülő" a család játszhat 720 nap, azaz közel 2 év.
6. példa Tíz különbözõ betût egymás után tíz borítékba helyezünk. Hányféleképpen lehet ezt tenni?
A megoldás. A javasolt helyzet eltér az előzőtől (5. példa). Valóban itt voltak emberek és székek - levelek és borítékok. Ugyanakkor itt és ott is meg kell tudnod találni, hogy hányféleképpen helyezhetsz el n elemeket n helyeken.
Az előző megoldás megismétlésével azt találtuk, hogy 10 vagy 9 · 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1 = 3,628,800 betűszó betűvel történő terjesztésének módja. Több mint 3,5 millió!
Amint látjuk, a feladatok feltételei eltérőek, és a megoldások és a kapott válaszok lényegében azonosak. Ebben a vonatkozásban célszerű ugyanazt a jelölést bevezetni az ilyen válaszokra.
Meghatározás Az első egymást követő n természetes számok termelését n jelöli!
Az n jele! "n" faktorikus "", amely az angol nyelvű szó szerinti fordításban "n tényezőkből álló". Több első értéket adunk n:
6! = 1 · 2 · 3 · 4 · 5 · 6 = 720, stb.
Nézzünk még néhány példát:
A megoldás. a) 3! = 1 # 8729; 2 # 8729; 3 = 6.
b) azóta 8729, 2, 8729, 3, 8729, 4, 8729, 5, 8729, 6, 8729, 7 és 5 = 1 8729, 2 8729, 3 8729, 4 8729, akkor 5! ki lehet venni a zárójelből, akkor kapunk 5 (6 # 8729; 7-1) = 1 # 8729; 2 # 8729; 3 # 8729; 4 # 8729; 5 # 8729; 41 = 4920.
8. példa A kifejezés egyszerűsítése :.
A megoldás. = 1 # 8729; 2 # 8729; 3 # 8729; ... # 8729; (n-1) # 8729; n # 8729; (n + 1); a = 1 # 8729; 2 # 8729; 3 # 8729; # 8729; (n-1) a rövidítés után n # 8729; (n + 1).
Hogyan készíthetünk egy általános kijelentést, amelynek konkrét esetei a 3., 5. és 6. példák megoldásai? Itt van az egyik lehetséges lehetőség.
ELMÉLET: n különböző elemeket rendelhetünk 1-től n-ig pontosan pontig! különböző módon.
A tételben leírt minden számítási módot 1-től n-ig gyakran egy adott n-elemkészlet permutációjának nevezik. Valóban feltételezhetjük, hogy mindegyik számozás csak a sor minden elemét helyezi vagy átveszi.
Az n elemek átáramlásait olyan kombinációknak nevezzük, amelyek csak az elemek sorrendjében különböznek egymástól.
Az n elemek halmazának permutációit Pn jelöli. Ezért a fenti tétel képlet formájában írható:
A combinatorics szaporítási szabályán kívül a kiegészítés szabályát néha használják: Annak érdekében, hogy megtaláljuk az A vagy B vizsgálat egyikének független elvégzéséhez szükséges összes lehetséges eredmény számát, az összes vizsgálati eredmény A számát és az összes vizsgálati eredmény számát V.
9. példa A pohárasztalon 5 ceruza és 3 toll van. Jegyzetek készítéséhez (írjon telefonszámot stb.) 5 db ceruzát vagy 1 db toll közül 1-et tehetünk, vagyis 5 opció közül választhatunk egy ceruzát és 3 opciót egy toll kiválasztásához. Mivel csak 1 tárgyat, ceruzát vagy tollat választunk, az összes lehetőség száma 5 + 3 = 8.
A sokszorosítási és kiegészítési szabályok bármely független tesztre vonatkoznak.
Összegezzük ismereteinket a legegyszerűbb kombinatorikus problémákkal. Megkaptuk az alapszabályt - a sokszorosítási szabályt, a geometriai modellt tekintettük - a lehetséges variánsok fája, új koncepciót vezettünk be - faktorikus, formulát készítettünk a permutációkról, amelyben ezt a koncepciót használjuk.