Legyen kisebb, mint egy félkör, ezért d (a, b)
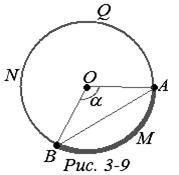
Legyen kevesebb, mint egy félkör, ezért d (A, B) az ív hossza. Az AOB középső szögének értékét az íves AMB-nél, és r (A, B) az AB szegmens hossza határozza meg. Mint tudják,
AOB (3-9. Ábra):
Az (1), (2) képletekből következik, hogy:
3. A gömb mozgása minden gömb izometrikus feltérképezése önmagára, azaz egy leképezés f. S ® S, amely megfelel a következő feltételnek: a gömb bármely A és B pontjának d (A, B) = d (f (A), f (B)). Ebből következik, hogy ebben az esetben r (A, B) = r (f (A), f (B)). Következésképpen az S gömb bármelyik mozgását a tér f0 mozgása generálja, és f0 (0) = 0. Ezzel ellentétben minden tér mozgása, amely az O invariáns pontot elhagyja, határozott mozdulatot hoz létre az S. gömbnek.
Ezért arra a következtetésre jutunk, hogy az S gömb mozgásainak halmaza olyan csoport, amely izomorf az O pont helyének H0 alcsoportjához a térmozgások csoportjában.
Két F, F 'Ì S mondat szerint kongruens vagy egyenlő, ha létezik az S gömb mozgása, amely az egyik számot átveszi egy másikra. Következésképpen az F, F ' Ì S egyenlõ, ha H0 egyenértékû.
4. A gömbbe S három pontot kapunk, A, B, C nem egy nagy körön. Három félgömböt definiálnak, amelyek mindegyike tartalmaz A, B, C pontokat, ezek közül kettő a félgömb széléhez tartozik. A három félgömb metszéspontját egy gömb alakú háromszögnek nevezik, amelynek csúcsai A, B, C AB körök, BC, AC nagy körök (kisebb félkörívek) az ABC gömb alakú háromszög oldalai.
Legyen ABC - gömbháromszög, a = d (B, C), b = d (A, C), egy = d (A, B) - a hossza az oldalán, a, b, g, illetve szögek BOC AOC és AOB.
Bizonyítsuk be a szinusz tételét egy gömb alakú háromszög számára.
Tétel. Tegyük fel, hogy a = d
Meg lehet bizonyítani, hogy a következő egyenlőség tartja, ami az ABC gömb alakú háromszög koszinus tételét fejezi ki:
Azt is bebizonyíthatod, hogy az ABC gömb alakú háromszög területét a képlet adja meg
hol van egy úgynevezett gömb alakú háromszög. Mivel a SABC> 0, a (8) képletből következik, hogy e> 0, azaz. Így bármely szférikus háromszög szögeinek összege nagyobb, mint p. Ez lényeges különbség a gömb geometriája között, mind az euklideszi sík geometriájától, mind a Lobachevsky sík geometriájától
A Lobachevsky geometria Poincaré modellje. (A francia tudós Henri Poincaré (1854-1912) - a legnagyobb matematikus leírt modell később a számukra felajánlott 1882 ..) által játszott szerepet a Lobacsevszkij síkban félig nyitott; az egyenes vonalak szerepe a benne lévő félköröknek felel meg, és a vonal mentén elhelyezkedő középpontok, valamint az erre a vonalra merőleges sugarak. Az átfedés szerepét inverz kompozíciókkal végezzük, ezeknek a félköröknek és a sugarak reflexióinak vonatkozásában. Minden Axióma euklideszi geometriát, a kivéve a axióma párhuzamos (ábra. 4-1 is), így ez a modell végezzük Lobachevskian geometria.
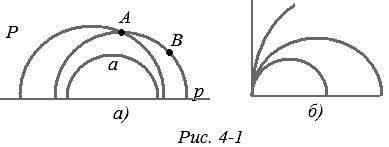
Részletesebben írjuk le ezt a modellt, és bizonyítsuk meg, amit mondtak. A szokásos Euklideszi síkra és a P határolt nyitott féltengelyére P-nek vesszük a p vonalvonalat. A P-fél-sík a Lobachevsky sík szerepét játssza; idézőjelekként "síknak" nevezzük. Pont a modell lesz a pont ennek a „sík”, azaz a. E. R. A félsíkot „közvetlen” a modellben elfogadott egyrészt szereplő P félkör akinek központok fekszenek a határvonal (ábra. 4-1, a). A modell "szegmense" AB a félkör A és B végpontjainak ívje.
Hangsúlyozzuk, hogy a "szegmens" vége nem lehet egy félkörkör vége, amely egy egyenes vonalat képvisel; annak végeit a határvonal mentén kizárják; A "sík" egy nyitott fél sík. Az "egyenes" pont két "sugarak" - két félköríves ív (kizárt végekkel) közös kezdetét szolgálja. A "szög" két, "közös" eredetű "sugarak" ábrája, amely nem szerepel egyetlen "egyenes vonalban" (4-1. Ábra, a).
Ezen "közvetlen" mellett vannak "közvetlen" is - ezek a félvonalak merőlegesek a határvonalra. Ezek a félkörök határai (4-1. Ábra, b). Ha a félkör közepét eltávolítják a határvonal mentén, és a félkör átmegy az adott ponton, akkor "kiegyenesedik", és a határérték a félvonalba kerül. Ezért a félvezetőket továbbra is a "közvetlen" modellek közé soroljuk félkörökként, mint a "végtelen sugarú félköröket". Ez lehetővé teszi, hogy eloszlassák az ilyen félvonalakkal kapcsolatos unalmas fenntartásokat, de emlékeznünk kell ennek konvencionálására, és készen kell állnunk arra, hogy ellenőrizzük az ilyen "félkörök" kimutatásait. (Az ilyen "egyenes" "szegmens" a szokásos szegmens, és a "sugarak" egy rendes sugár, a másik a szegmens, a határvonal kizárt végével.)
Most ebben a modellben vizsgáljuk azokat az axiómákat, amelyekben a szegmensek és szögek egyenlőségének fogalma nem lép be.
Az egyenes vonalú párhuzamos vonalak axiómája az ilyen axiómákra utal. Ebben a modellben nyilvánvalóan nem teljesül: egy "A" vonal mentén fekvő A ponton végtelen sok "egyenes vonal" halad át, amelyeknek nincsenek közös pontjai a (4-1.
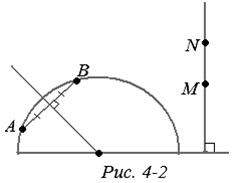
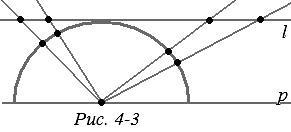
Minden olyan axióma, amely a pontok és a szegmensek vagy pontok és vonalak közötti kapcsolatról, a pontok és a vonalak kölcsönös elrendezéséről szól, itt elégedettek. Így a 3. ábrán. A 4-2. Ábra egy szegmens létrehozását mutatja meghatározott célokkal. Ezt követõen egy félkört veszünk, amely a modellben "egyenes vonalat" képvisel. Ehhez a félkörhöz egy vonalat rajzolunk, amely párhuzamos a határvonalral. Félkör alakú keretet helyezünk a középpontról az egyenes vonalra (4-3. Ábra). A vonal és a félkör közé, azaz az "egyenes" modellhez egy-egy rendelés-megőrző egyeztetést kapunk. Az axiómákban kifejezett összes tulajdonság ugyanaz lesz. Nyilvánvalóan a "közvetlen" modelleket ábrázoló félvonalakra is sor kerül. A sík felosztásának axiómája is teljesül. "Egyenes" - egy félkör - osztja a síkot két területre - a belső és a külső. Ez lesz a "fél-sík" a mi modellünkben. Az egyiktől a másikig nem lehet áthaladni semmilyen ív anélkül, hogy átlépné az "egyenes vonalat" - a félkört elválasztva.