A jelek entrópiájának tesztelése - online absztrakt adatbázis
Ábra. 2. Feltételes entrópia
3. Közös entrópia - az átlagos információmennyiség a továbbított és a fogadott szimbólumok párjánként (3. ábra).
H (X / Y) = H (X) + H (Y / X) = H (X) + H (Y / X) = H (X) + H (Y) X × Y).
4. A kölcsönös entrópia a statisztikailag függő üzenetek közös megjelenésének entrópiája (4.
Ábra. 3 Közös entrópia
Ábra. 4. Kölcsönös entrópia
A gyakorlatban gyakran vannak egymástól függő szimbólumok és üzenetek. Például a szöveges üzenetek küldésekor nemcsak betűket, hanem bizonyos szavakat is tartalmaznak. Ebben az esetben minden betű és a betűk kombinációja eltérő előfordulási valószínűséget eredményez a szövegben. A feltételes entrópia figyelembe veszi az események kapcsolatát a feltételes valószínűségeken keresztül.
Tekintsük a 2. ábrán látható áramkört. 5:
Ábra. 5. Üzenetek
Az üzenetforrás X - olyan üzeneteket hoz létre, amelyek elemei a forrásaláírás karakterei. az előfordulás valószínűsége, amelynek kimenete egyenlő p (x1), p (x2) értékkel. p (xm), míg:
A forrás entrópiája az elsődleges ábécé szimbólum megjelenésének bizonytalansága az üzenetforrás kimenetén, és az összefüggés határozza meg:
()
Az üzenetvevõ Y - olyan üzeneteket fogad, amelyek elemei a vevõ ábécéjének szimbólumai. az előfordulás valószínűsége, amelynek bemenete egyenlő p (y1), p (y2) értékkel. p (ym), míg:
A vevõ entrópiája a szimbólum üzenetek vételi bemenetén megjelenõ bizonytalanság, miután megjelenik a forráskimenetnél, és amelyet a reláció határoz meg:
Ha a kommunikációs csatornában nincs adatvesztés (nincs interferencia, hiba stb.), Akkor az yi szimbólum megfelel a xi szimbólumnak. Egyébként xi a lehetséges y1, y2 bármelyike lehet. ym. megfelelő valószínűségekkel.
Veszteségek hiányában: H (X) = H (Y). Interferencia jelenlétében megsemmisítik az információk egy részét. Ebben az esetben az információvesztés meghatározott és általános feltételes entrópia révén határozható meg.
Kényelmes kiszámítani az általános feltételes entrópiát csatorna mátrixok (az átmeneti állapotok mátrixa) segítségével.
A csatorna információcsökkenését a forrásból vagy az üzenetvevőtől lehet becsülni.
Vegye figyelembe a veszteségek meghatározásának sorrendjét a forrásoldaltól (a továbbított jel ismert). Ebben az esetben a feltételes valószínűség p (yj / xi) azt a valószínűséget jelenti, hogy az yj üzenet akkor érkezik, amikor az xi üzenetet továbbítjuk. A csatorna mátrix a táblázatban látható formában van. 1.
Az átlóban lévő helyszín valószínűsége a helyes átvitel valószínűségét jellemzi, a többi hamis. A vevőkészülék bemenetére vonatkozó egyenirányú jelek esetén a teljes feltételes entrópiát a következő képlet adja meg:
A vételi bemeneten a nem feltételezhető jelek esetében a teljes feltételes entrópiát a következő képlet adja meg:
Egy speciális feltételes entrópia, amely meghatározza az y1 jelnek tulajdonítható veszteségeket. egyenlő:
Példa 1. Számítsuk ki az üzenet forrásának entrópiáját, amely két 0 és 1 szimbólumot eredményez p (0) = 3/4, p () = 1/4 valószínűséggel és feltételes valószínűségekkel: p (0/0) = 2/3, p (/ 0) = 1/3, p (0/1) = 1, p (/ 1) = 0. azaz 1 után mindig 0 van.
Megoldás: Az egymástól függő, nem egyenetlen elemek esetében az entrópia:

2. példa. Határozza meg az üzenetforrás entrópiáját, ha a vevőegység bemenetére a szimbólumok előfordulási valószínűségei: P (b1) = 0,1; P (b2) = 0,3; P (b3) = 0,4, P (b4) = 0,2, és a csatorna mátrix formája:
A valószínűség összege azonos feltételek mellett
Megoldás: Határozza meg a forrás entrópiáját
.
= 0,1 × 0,01 + 0,3 × 0,98 + 0,4 × 0,01 + 0, × 2 × 0,01 = 0,301;
0,1 × 0 + 0,3 × 0 + 0,4 × 0,98 + 0,2 × 0,02 = 0,396;
0,1 × 0 + 0,3 × 0 + 0,4 × 0,01 + 0,2 × 0,97 = 0,198;
A forrás entrópiája:
3. példa Határozza meg a kommunikációs csatornán átadott üzenetek forrásának entrópiáját és feltételes entrópiáját, amely egyenirányítható szimbólumokat tartalmaz, ha a csatorna interferenciájának hatását mátrix írja le:
.
Megoldás: Egy üzenetben az azonosítható karakterek esetén az üzenetforrás entrópiai:
A teljes feltételes entrópia:
=
4. példa. Határozza meg az üzenetvevõ entrópiáját, ha az a1, a2 és a3 szimbólumok elõfordulási valószínűsége az üzenetforrás bemenetén P (a1) = 0,5; P (a2) = 0,3 és P (a3) = 0,2, és a csatorna mátrix formája:
,
Megoldás: A vevõ entrópia:
.
A jelek megjelenésének valószínűsége a vevő bemeneténél
;
;
.
.
2. A FOLYAMATOS ÜZENETEK FORRÁSA
Egy folyamatos forrás (jel) információ tulajdonságainak leírására a differenciál entrópia fogalmát használjuk. Ennek eléréséhez a diszkrét üzenetek entrópiájára vonatkozó képletet használjuk. A valószínűségi sűrűségfüggvény grafikonjával (6. Ábra) írhatunk p (xi) =?. Ahol p (xi) az a valószínűség, hogy x az i-os kvantálási lépésen belül helyezkedik el.
Ábra. 6. A valószínűségi sűrűségfüggvény grafikonja
Ebben az esetben az entrópia kifejezését a formában lehet ábrázolni
Átmegyünk a határig:
.
A folyamatos üzenetforrás teljes entrópiája két kifejezésből áll, amelyek közül az egyiket a terjesztési törvény határozza meg, a második pedig a kvantálási lépés meghatározó állandója, amely befolyásolja a mérések pontosságát. A kifejezés ezen kifejezése állandó komponenst definiál, és kizárható a megfontolásból.
Az első ciklus értékét a disztribúciós törvény határozza meg, és jellemzi a folyamatos forrás differenciál entrópiáját (mivel f (x) a valószínűségi sűrűség vagy a differenciálódási törvény)
A differenciál entrópia része a folyamatos üzenet forrása entrópiájának, amely az x (t) jel valószínűségi sűrűségétől függ. a forrás kiadja.
A fizikai jelenségek és folyamatok különböző osztályai megfelelnek a különböző terjesztési törvényeknek. A folyamatos jeleket teljesen elosztási törvények (integrál vagy differenciál) jellemzik. Valódi jelek bizonyos korlátozásoknak vannak kitéve, például: átlagos teljesítmény (fűtőberendezések); pillanatnyi vagy csúcsteljesítmény (túlterhelés).
Mivel az eltérés entrópia függ sűrűségfüggvénye definiáljuk, melyek törvény szerint maximális. E. A, amely a valószínűségi eloszlás, a teljesítmény jelet egy előre meghatározott maximális entrópia. Ahhoz, hogy megtalálja a maximális értéket az entrópia kell használni a variációs tétel segítségével Lagrange szorzók, ha a feltételek a normalizáció és az átlagos négyzetes ugyanaz:
; .
Az egyenletek megoldásával szimmetrikus normál terjesztési törvényt kapunk
Ha az átlagos teljesítmény nem korlátozott
akkor megkapjuk az egységes forgalmazási törvényt.
Meghatározzuk a differenciál entrópiát egy normál eloszláshoz, azaz egy korlátozott átlagos teljesítményű jelhez. A variációs probléma megoldásából kapott normál eloszlás szimmetrikus. Ha az x = y-mx értéket a differenciál entropia integráljára cseréljük. akkor az integrál nem változik, ezért az entrópia nem függ a matematikai elvárástól, és egyenlő a centrált random változó entrópiájával.
Határozza meg az entrópia maximális értékét:
A normál eloszlású differenciál entrópia:
A normál eloszlás teljes entrópiája:
Ha figyelembe vesszük, hogy h (x) a függvény [-log2 f (x)] függvény matematikai várakozása egy f (x) sűrűségű x véletlen változótól, akkor írhatunk.

A központi határérték tételének megfelelően a normál elosztási törvények az úgynevezett Gauss-véletlen folyamatok vagy valós jelek széles körére vonatkoznak.
A fehér zaj a leginkább "rosszindulatú" tulajdonságokkal rendelkező akadály, azaz a káros információ maximális mennyiségét adja át egy adott átlagos teljesítmény mellett, és lehetővé teszi a legrosszabb esetben a számítások egyszerűsítését.
Annak érdekében, hogy a korlátozott csúcsteljesítményű jelnek legyen maximális informatikussága, egyenletes eloszlás szükséges (9. Meghatározzuk a differenciál entrópiát az egyenletes eloszláshoz, vagyis egy korlátozott csúcsteljesítményű jelhez. Ha P-csúcs teljesítmény, akkor - a maximális amplitúdó. A differenciál entrópiának a korlátokkal való egyenlőtlenségekre vonatkozó egyenlete a következőképpen alakul:
A differenciál entrópia az egyenletes eloszlás szempontjából:
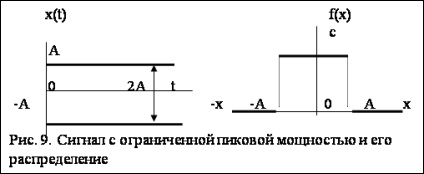
Egy egyenletes eloszlású jel teljes entrópiája:
ahol m a kvantálási szintek száma.
Meghatározzuk az exponenciális eloszlás differenciál entrópiáját. Ezt az eloszlást széles körben használják a rádiós elektronikus berendezések hibáinak intenzitására
Az exponenciális eloszlás teljes entrópiája:
2. Yaglom AM Yaglom IM Probléma és információ. M. 1957.
3. Shannon K. Működik az információelmélet és a kibernetika elméletéről. - M. Ed. külföldi. Irodalom. 1963. - 830. o.
4. Wolkenstein, MV entropia és információ. - M. Nauka, 1986. - 192 oldal.
5. Tsymbal VP Információelmélet és kódolás. - M. Vysshcha Shkola, 1977. - 288 o.
6. Probabilisztikus módszerek a számítástechnikában. / Ed. AN Lebedev, E. Chernyavsky. -M. Felsőoktatás wk. 1986.
Sedov E.A. Az információ, az energia és a fizikai entrópia közötti kapcsolat az irányítás és az önszerveződés folyamatában. Információ és menedzsment. M. Nauka, 1986.