A funkciók aszimptotikus viselkedésének összehasonlítása

A második figyelemre méltó határ

Az első figyelemre méltó határ

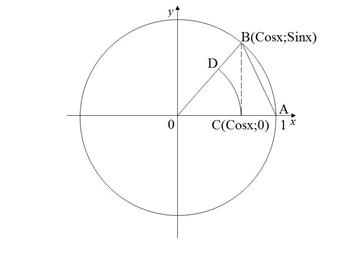
Bizonyítás. Ezt először megmutatjuk. Mivel az egyenlőtlenség minden funkciója egyenletes, az esetet tekintjük.

Nyilvánvaló, hogy az ívelt szektor OCD területe kisebb, mint az OAB háromszög területe, és kisebb, mint az OAB görbe szektor területe. A görbe ágazat területének képletét használjuk: (r a sugár, x a központi szög). majd

Az utolsó egyenlőtlenség minden részét x-vel osztjuk meg, és kettővel megszorozzuk. A legutóbbi egyenlőtlenség minden részének határait elérve megkapjuk, amit be kellett bizonyítani.

Cseréljük az utolsó határt, megkapjuk

Állítás Ha és, akkor

Az utolsó példában kaptuk.

a) Egyenértékű funkciók.

Ha egy pont egy bizonyos lyukas szomszédságában a függvény formában reprezentálható, akkor az u függvények egyenértékűek az u-val és írni

Assertion Ha valaki, akkor

abban az időben és csak akkor, amikor.

Például, mert; , mivel.

Az ekvivalens funkciók táblázata

Tétel, ha és majd

b) Az infinitezimális függvény fogalma a másikhoz képest.

Ha a pont bizonyos megszakított szomszédságában a függvény formában is reprezentálható, akkor a függvényt végtelenül kicsinek mondják, mint amikor írják.

Assertion Ha valaki, majd akkor, és csak akkor, amikor.

1. példa); 2) mikor.

Ha u mindkettő egyáltalán nem infinitezimális, akkor azt mondjuk, hogy van egy végtelen, magasabb rendű, mint a.

A szimbólum néhány fontos tulajdonsága.

Bizonyítsuk be például ezt. Valóban, mivel ha mindkettő végtelen, akkor is infinitezimális # 9632;

4 Folyamatos funkciók