Véletlen szám generáló algoritmusok elmélete
A mennyiséget véletlenszerűnek nevezik, ha valamilyen teszt (tapasztalat) kimenetelétől függ, és minden elemi eredményhez egyetlen értékű. Egy véletlen változót diszkrétnek neveznek. ha az összes lehetséges értékének halmaza véges.
Geometriailag a diszkrét CB összes lehetséges értéke a számtengely véges pontrendszerét képviseli.
Legyen X diszkrét CB. amelyek lehetséges és csak lehetséges értékei az x1 számok. x2. ..., xn.
ezeknek az értékeknek a valószínűsége (vagyis pi a valószínűsége az eseménynek, hogy X az xi) /
Az események X = xi (i = 1, 2, ..., n) nyilvánvalóan az események teljes csoportját alkotják
A diszkrét CB és a valószínűségeik közötti összes lehetséges érték közötti megfelelést egy adott CB terjesztési törvényének nevezzük.
Egy diszkrét SV esetében a terjesztési jogot kényelmesen adják meg a táblázat
Az első sor tartalmazza a CB összes lehetséges értékét, a második pedig a valószínűségeit.
Egy X véletlen változót folyamatosnak nevezünk, ha minden lehetséges értéke teljes egészében kitölt egy bizonyos véges vagy végtelen intervallumot 
A CB X jellemzésére az elosztási függvény
ha az elosztási függvény értékeinek száma megszámolható, akkor X egy diszkrét CB, ha a végtelen folyamatos CB.
Az elosztási funkció tulajdonságai:
4) ha x1
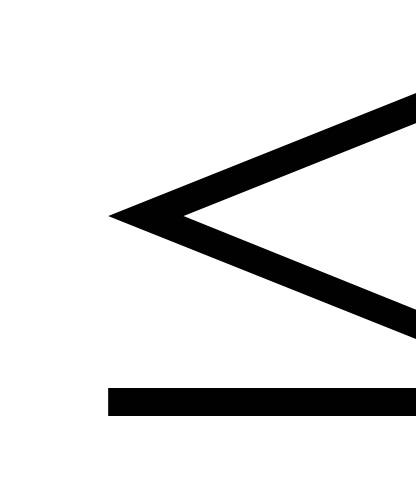
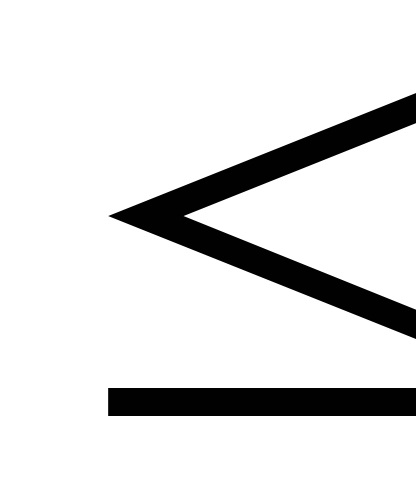
5) P (x1
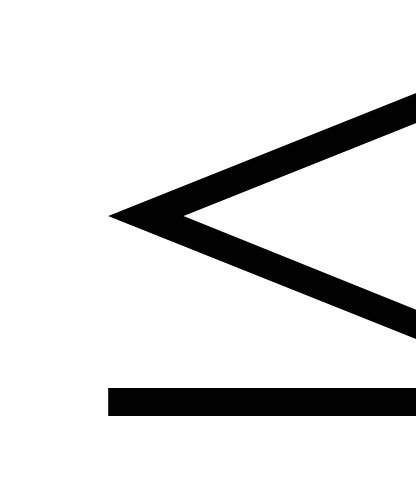
Tegyük fel, hogy a folytonos CBX esetében a Ф (х) eloszlásfüggvényének folyamatos deriváltja van
f (x) a valószínűségi sűrűség (adott eloszlás) vagy a CB X differenciálódási törvény.
Pszeudo-véletlen számok sorozata
Véletlen és pszeudo-véletlen számok, olyan számok, amelyek valamilyen véletlen változó megvalósításának tekinthetők. Rendszerint egy 0,1-es intervallumon egyenletesen elosztott véletlen változó megvalósulását értjük, vagy ezeknek a megvalósításoknak a megközelítését, amelyeknek véges számú számjegye van a reprezentációjukban. Ilyen szűk értelmezés esetén egy véletlenszám (dp) lehet véletlen számjegyből (sf) álló szám. S. c. a p-számjegyű számrendszerben egy olyan kísérlet eredménye, amelyen a p-nek valószínűsíthető kimenetele (mindegyik kimenet egy p-számjegynek felel meg). Kísérleteket kapni minden egyes s. c. feltételezik, hogy függetlenek.
Egy forrás innen. c. Kezdetben a népszámlálás és a számok egyéb tábláinak eredményei kísérletileg. Az első táblázatok. c. 1927-ben összeállították a matematikai statisztikák szükségleteivel összefüggésben (véletlenszerű kiválasztás szükségessége a kísérlet tervezésében). Később, a statisztikai tesztek módszerével kapcsolatban speciális kísérleti eszközök jöttek létre - szenzorok vagy generátorok c. h) a legtöbb esetben az elektronikus eszközök zajt használják.
A statisztikai tesztek módszere kidolgozásával a pszeudo-véletlen számok koncepciójának kialakulása is társul (alszekció). Ez utóbbit adott képlet alapján (algoritmussal) számolhatjuk ki, de tulajdonságaiknak közel kell válniuk c-hoz. h. A leggyakoribb algoritmusok, amelyekben az elkövetkezõ számok az elkövetkezõ számokból számolnak. Az így nyert szekvenciáknak olyan periódusa van, amely lényegében megkülönbözteti őket a c. h. Algoritmusok megkapjuk az n. h. Több nem vizsgálták behatóan, de a módszer A statisztikai számítások előnyben részesíteni vizsgálati n. h. t. k. tulajdonságait a szekvencia N. h. A teszt segítségével vizsgáltuk számítások és kísérleti eszközök biztosítják új szekvencia. h) minden használat során.
A véletlen egy adott tartományból származó mennyiség, amelynek előfordulási valószínűségét a terjesztési törvény funkciója határozza meg. Példa: egy diszkrét véletlen változó egyenletes eloszlása az 1-6 tartományban - valószínűség 1/6.
Valóban véletlen érték elérése csak akkor lehetséges, ha fizikai vagy kémiai folyamatot használnak meghajtó mechanizmusként. A számítógép segítségével pszeudo-véletlen szekvenciák nyerhetők. Számukra jellemző, hogy ugyanazok a kiindulási értékek kiválasztása azonos szekvenciák létrehozásához vezet, és van olyan N, hogy az N + 1 kifejezés egyenlő a szekvencia első időtartamával.
C-ben vannak olyan funkciók, amelyek lehetővé teszik, hogy létrehozzon egy pszeudo-véletlen egész számsorozatot, állítsa be a sor kezdeti értékét, a kezdeti értéket véletlenszerűen állítsa be (a rendszertől függően).
Ezután a pszeudo-véletlen számok előállítására szolgáló módszereket veszik figyelembe.
6.1. Közepes négyzetek módszere
a) Tetszőleges egész számot választunk ki a 2k-es számjegyű x0 számot. amely négyszögletű, az eredmény egy 4 k-os szám, amelyből kiválasztják az átlagos 2 k-os számjegyeket, amelyek a következő véletlen számot alkotják. Az eljárást megismétlik a szükséges számú alkalommal.
b) Két tetszőleges 2k-értékű számot veszünk, amelyeket megszorozzuk és kiegészítünk a 4k-értékkel. Középről 2k számjegyet veszünk, a következő számot a kapott szám és az előző termékből kapjuk.
Az így kapott számok pszeudo-véletlennek tekinthetők, mert a középső jelek függenek a szélsőségesektől, amelyeket eldobnak.
6.2. A multiplikatív módszer
A C és m konstansok adottak. Véletlen számot veszünk, a következő pszeudovéletlen szám az aktuális szám, megszorozva C-vel osztva, modulus szerint.
6.3. Adalék-módszer (Fibonacci-generátor)
Az m egész szám definiálva van. Két egész számot veszünk. A következő szám megegyezik a két előző összegével, a modulo-hoz.
6.4. Lineáris módszer
Ezt egy [j], j∈ [1, k] és m egész számú egész számkészlet határozza meg. Kezdetben minden számot veszünk. A következő pszeudo-véletlen szám megegyezik a [j] xi + 1-j osztott modulo produkciók 1-nél nagyobb összegével.
6.5. Kombinált módszer
Vegyünk egy egész 2 k -értékű x0 számot. Száma
x0 'az x0 négyzet utolsó 2k-ja,
x0 "a Cx0 'termékének első 2k része (C egy egész szám),
x0 '' 'az x0' 'négyzet első 2k számjegye,
x0 '' '' az x0 '' 'x0' ''
A pszeudo-véletlen szekvencia-generátor minősége meghatározható pseudorandom számok hisztogramjával. a terjesztési törvény egységes, az oszlopok magassága megközelítőleg azonosnak kell lennie.