Oktató matematikában, fizikában, programozásban, Kharkovban
Ennek a funkciónak a tartománya minden szám, kivéve azokat, amikor a nevező 0.
Az egyenlőtlenséget az intervallum módszerrel oldjuk meg.
Megoldjuk a kiegészítő egyenletet.
Az ismert mennyiségeket az egyenlet jobb oldalára helyezzük át.
Ennek az egyenletnek a választja:
.
Megjegyezzük a talált kritikus pontokat és a megfelelő intervallumokat a valós vonalon.
Az eredményül kapott oldatot az ábrán mutatjuk be.
A függvény megvizsgálásához megtalálja az első származékot
A konstans és a függvény termékének származéka megegyezik a konstans termékével a függvény deriváltjával.
A hányados származékának képletét használjuk.
Végezzük el a közös tényezőt.
Változtassuk meg a kifejezések jeleit az ellenkezőjére.
A termék mínusz jeleit veszünk.
A második származék az első származék származéka.
A konstans és a függvény termékének származéka megegyezik a konstans termékével a függvény deriváltjával.
A konstans és a függvény termékének származéka megegyezik a konstans termékével a függvény deriváltjával.
A hányados származékának képletét használjuk.
A hatalmak tulajdonát használjuk.
A termék származékának képletét használjuk.
Használjuk azt a szabályt, hogy megtaláljuk a származékot komplex funkcióhoz.
Kinyitjuk a zárójeleket a szaporodó törvény szerinti multiplikációval
Végezzük el a közös tényezőt.
A hatalmak tulajdonát használjuk.
Változtassuk meg a kifejezések jeleit az ellenkezőjére.
A termék mínusz jeleit veszünk.
Az x tengely metszéspontja:
A metszéspontok megtalálása az abszcissza tengelyen, a funkciót nullára állítjuk.
A frakció eltűnik, ha a számláló nulla.
Az egyenlet bal és jobb oldalát az ismeretlen koefficiensével osztjuk el.
A tengellyel metszéspontok
:
Meghatározzuk az argumentum értékét, amelynél a függvény nevezője eltűnik
Az ismert mennyiségeket az egyenlet jobb oldalára helyezzük át.
Hegyes aszimptoták: nem
Egy adott függvény határvonala a végtelenben megegyezik a 0 számmal
A kritikus pontok feltérképezéséhez az első származékot nullázzuk, és a kapott egyenletet megoldjuk.
Változtassuk meg a kifejezések jeleit az ellenkezőjére.
A frakció eltűnik, ha a számláló nulla.
Tehát a válasz ez:
.
Az ismert mennyiségeket az egyenlet jobb oldalára helyezzük át.
Az egyenlet bal és jobb oldalát az ismeretlen koefficiensével osztjuk el.
Tehát a válasz erre az esetre: nincs megoldás.
Lehetséges inflexiós pontok: nem
Ha lehetséges inflexiós pontokat találunk, akkor a második származékot nullázzuk, és a kapott egyenletet megoldjuk.
A frakció eltűnik, ha a számláló nulla.
Az egyenlet bal oldala csak pozitív értékeket vesz fel.
Válasz: nincs megoldás.
Szimmetria az ordinát tengelyéhez képest: a függvény egyenletes, a gráf szimmetrikus a tengely körül
.
F (x) függvényt akkor is mondhatjuk, ha f (-x) f (x).
A termék mínusz jeleit veszünk.
Szimmetria a származáshoz képest: nem
Egy f (x) függvény furcsa, ha f (-x) + f (x).
A termék mínusz jeleit veszünk.
Hasonló feltételeket idézünk.
A maximális ponton való áthaladás. a függvény deriváltja a pluszról a mínuszra ugrik.
A relatív maximális értéke (0,0).
A táblázat adatait a koordináta síkján kell ábrázolni.
A függvényvizsgálat eredményeinek felhasználásával grafikunkat készítünk.
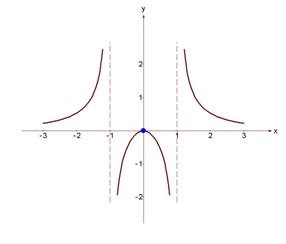
A függvény értékkészlete: az összes valós szám halmaza
A legkisebb érték és a legnagyobb érték: a funkciónak nincs a legkisebb és legnagyobb értéke