Egylapos hiperboloid, kanonikus egyenlete; egyenes vonalú generátorok
egysávú hiperboloid x 2 / a 2 + y 2 / b 2 - z 2 / c 2 = 1 a> 0, b> 0, c> 0; Keresztbe. koordináta osiploskostyami x = 0, y = 0, z = 0 és hiperbolák y 2 / b 2 - Z 2 / c 2 = 1 x 2 / a 2 - Z 2 / c 2 = 1, és ellipszoid x 2 / a 2 + y 2 / b 2 = 1. A szakaszok SSB hiperboloid síkok Z = H mindig kapott ellipszisek x 2 / a 2 + y 2 / b 2 = 1 + H 2 / C 2 a tengelyek és.
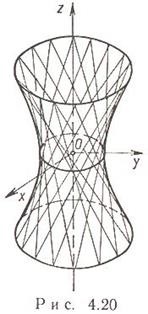
a = b egy órás tengelyű óriási forradalmi hiperboloid.
Az egyik lap hiperboloidjának szekciói ellipszis, parabola vagy hiperbola vagy egy pár egyenes (négyszögletes generátor).
Tetszőleges ponton át két iránytű generátor vezet át irányító vektorokkal és ahol:
Különösen, ha egy pontot választunk a torok ellipszisén, akkor az egyenlõs generátorok egyenletei:
Kétlapú hiperboloid, kanonikus egyenlete.
két-sheeted hiperboloid x 2 / a 2 - y 2 / b 2 - Z 2 / c 2 = 1, a> 0, b> 0, c> 0; X = H A cím ellipszis x 2 / a 2 + z 2 / b 2 = -1 + H 2 / C 2 a tengely b * root (H 2 / a 2 -1) és c * root (H 2 / a 2 - 1). Ha h = a, akkor kapunk pontokat (± a, 0,0) - a két üreg csúcsai. A koordináta keresztmetszeteiben z = 0 és y = 0, akkor megkapjuk a x 2 / a 2 - y 2 / b 2 = 1 és a x 2 / a 2 - z 2 / c 2 = 1 hiperbolákat.
a = b egy kétlapos, forradalmi hiperboloid az Oz tengely körül.
Kétlapú hiperboloidok szelvényei síkokkal: ellipszis, hiperbola vagy parabola vagy pont.
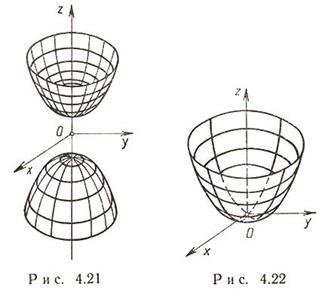
Elliptikus paraboloid, kanonikus egyenlete.
elliptikus paraboloid x 2 / a 2 + y 2 / b 2 = 2pz a> 0, b> 0;
p = q a forradalmi paraboloid az Oz tengely körül.
Az elliptikus paraboloidok síkokból álló része ellipszis vagy parabola vagy pont.
Hiperbolikus paraboloid, kanonikus egyenlete. Hiperbolikus paraboloidok egyenes vonalú generátorainak családjai.
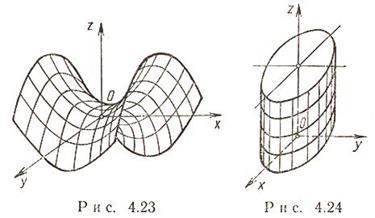
hiperbolikus paraboloid x 2 / a 2-y 2 / b 2 = 2pz a> 0, b> 0;
Hiperbolikus paraboloidok keresztmetszetei síkokkal - vagy egy hiperbola, vagy egy parabola vagy egy pár egyenes (egyenirányú generátor).
Egyenes vonalgenerátorok
Két egyenes vonalú generátor halad át minden ponton:
A forradalmi felület olyan felület, amelyet egy bizonyos síkvonal elforgatása képez, amely a vonal síkjában fekvő egyenes vonal körül van.
A forradalmi felület egyenletének levezetéséhez egy koordináta-rendszert kell kiválasztani. Annak érdekében, hogy a forradalmi felület egyenlete egyszerűbb legyen, a forgás tengelye az egyik koordinátatengelynek tekinthető.
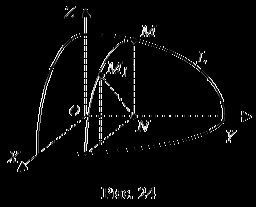
Adjuk meg az L görbét a Oyz koordináta-síkban az F (Y, Z) = 0 egyenlet segítségével (24. ábra). Forgassa el az L görbét az Oy tengely körül. Felületet kapunk. Legyen M (x, y, z) a kapott felület tetszőleges pontja. majd
. de mert ha az M1 pontot negatív applikátorral vesszük, akkor
Ezért van Y = y, és az M (x, y, z) pont koordinátái megfelelnek az egyenletnek
A (62) egyenlet a forradalom felületének szükséges egyenlete.
Így. hogy az L vonalnak a Oyz síkban való elforgatásával létrejövő egyenletet az Oy tengely körül körvonalazva megkapjuk, ehhez a vonal egyenletéhez z helyettesíteni kell
Hasonló szabályok alkalmazandók a más koordináta tengelyek körüli síkvonalak forgatásával kapott felületek egyenleteire is.
a másodrendű hengerek: egy elliptikus henger x 2 / a 2 + y 2 / b 2 = 1 a> 0, b> 0; hiperbolikus henger x 2 / a 2 - y 2 / b 2 = 1 a> 0, b> 0; parabolikus henger y 2 = 2px; egy pár egymást metsző síkok a2x2-b2y2 = 0 a> 0 b> 0, vagy egy pár egymással párhuzamos síkokban egybeeső X-a = 0 a> = 0; az x 2 + y 2 = 0 vonal
x2 / a2-y2 / b2-z2 / c2 = 0 a> 0, b> 0, c> 0; Kereszteződés pl. z = h -> x2 / a2 + y2 / b2 = 1. A szekcionált síkok x = 0, y = 0, van egy pár keresztbe vonalak y 2 / b 2 - Z 2 / c 2 = 0; x 2 / a 2 - z 2 / c 2 = 0 ill.