Bizonytalanság, információmennyiség és entrópia - stadopedia
Claude Shannon, az információelmélet alapítója meghatározta az információkat. mint eltávolított bizonytalanság. Pontosabban, az információszerzés szükséges feltétele a bizonytalanság megszüntetéséhez. A választás helyzete bizonytalanságot eredményez. A bizonytalanság kiküszöbölése során megoldott feladat a megválasztott lehetőségek számának (a sokféleség csökkenése) csökkenése, és végül az esetleges lehetséges lehetőségek közül egy adott helyzet megválasztása. A bizonytalanság megszüntetése lehetővé teszi a tájékozott döntések meghozatalát és cselekvését. Ez az információ ellenőrző szerepe.
Képzeld el, hogy mentél a boltba, és kérte, hogy eladjon egy rágógumit. Az eladó, aki 16 fajta rágógumit mond, bizonytalan. További információ nélkül nem tudja teljesíteni kérését. Ha megadott mondjuk - «Orbit», és 16 a kezdeti beállítások eladónő látja most már csak 8, akkor csökkenti a bizonytalanságot kétszer (előre néz, azt mondják, hogy a csökkentés a bizonytalanság kétszeresének felel kap 1 bit információ). Ha tompán filozofizálni, csak mutatta az ujját az ablakra - ez! - a bizonytalanság teljesen eltűnt. Ismét előretekintve, mondjuk, hogy ebben a példában ezt a gesztust közöltük az értékesítővel 4 bites információval.
A maximális bizonytalanság helyzete több, valószínűleg azonos alternatíva (változat) jelenlétét feltételezi, azaz egyik lehetőség sem előnyösebb. Ráadásul az egyenletlenebb változatok is megfigyelhetők, annál nagyobb a bizonytalanság, annál nehezebb egyértelmű választást tenni, és annál több információra van szükség ahhoz, hogy ezt meg lehessen szerezni. Az N változatok esetében ezt a helyzetet a következő valószínűségi eloszlás írja le:.
A minimális bizonytalanság 0, azaz 0. ez a helyzet tele van bizonyossággal. ami azt jelenti, hogy a választás megtörtént, és minden szükséges információt megkapnak. A teljes bizonyossággal járó valószínűségek eloszlása a következő:
Az információelméletben a bizonytalanság mértékét jellemzõ mennyiséget a H szimbólum jelöli, és entrópiának nevezik, pontosabban az információ entrópiaként.
Az entrópia (H) a bizonytalanság mértéke, bitben kifejezve. Hasonlóképpen, az entrópia is tekinthető egy valószínűségi változó eloszlásának egységességének.
Ábra. 8. Entrópia viselkedése két alternatíva esetén.
A 8. ábra két alternatíva esetében az entrópia viselkedését mutatja, a valószínűségeik arányának változásával (p, (1-p)).
Entrópia eléri a maximális értéket ebben az esetben, amikor a két valószínűség egyenlő egymás között és egyenlő ½, a nulla értéket az entrópia megfelel az esetek (p0 = 0, p1 = 1) és a (P0 = 1, P1 = 0).
Az I információmennyiség és a H entrópia ugyanazt a helyzetet jellemzi, de minőségi szempontból ellentétes oldalakon. Én vagyok a bizonytalanságot eltávolító információk mennyisége H. Leon Brillouin meghatározása szerint az információ negatív entrópia (negentropia).
Ábra. 9. Az entrópia és az információ mennyiségének összefüggése.
Amikor a bizonytalanság teljes mértékben eltávolodik, a kapott információ mennyisége megegyezik a H. kezdetben meglévő bizonytalanságával.
A bizonytalanság részleges megszüntetésével a kapott információ mennyisége és a fennmaradó bizonytalan bizonytalanság a kezdeti bizonytalanság összege. Ht + Ez = H.
Emiatt a H entrópiának kiszámításához az alábbi képleteket is bemutatjuk: az I. információ mennyiségének kiszámítására szolgáló képletek. amikor a bizonytalanság teljes eltávolításáról van szó. H számukra helyettesíthető I.
Általában. a H entrópiája és a bizonytalanság eltávolításával kapott információ mennyisége függ az N megfontolt változatainak kezdeti számától és az a priori valószínűségektől, hogy mindegyikük megvalósuljon P: 0. p1. ... pN-1>. azaz H = F (N, P). Az entrópia kiszámítása ebben az esetben Shannon képlet szerint történik. amelyet 1948-ban a "Matematikai elmélet kommunikációja" című cikkében javasoltak.Ebben az esetben. ha minden változat egyformán valószínű. A függőség csak a figyelembe vett változatok számától függ; H = F (N). Ebben az esetben a Shannon formula jelentősen leegyszerűsíti és egybeesik a Hartley-formulával. Először 1925-ben az amerikai mérnök Ralph Hartley javasolta, azaz. nem 20 évvel korábban.
A Shannon formula a következő alakú:
Az (1) képlet mínusz jele nem jelenti azt, hogy az entrópia negatív mennyiség. Ezt azzal magyarázza, hogy pi £ 1 definíció szerint, és az egynél kevesebb logaritmus negatív. A logaritmus tulajdonsága szerint. ezért ez a képlet a második változatban írható, mínusz nélkül az összeg jele előtt.
úgy értelmezik, mint egy bizonyos mennyiségű információt. Az i. Verzió végrehajtása során kapott eredmény. A Shannon-képletben az entrópia egy átlagos jellemző - a 0. i1, ... IN-1> véletlen változó eloszlásának matematikai elvárása.
Példát mutatunk az entrópia kiszámítására a Shannon-képlet alapján. Tegyük fel, hogy az intézményben az alkalmazottak összetétele a következőképpen oszlik meg: ¾ - nők, ¼ - férfiak. Ezután a bizonytalanságot, például arról, hogy kivel találkozol először, amikor az intézménybe jár, az 1. táblázatban bemutatott műveletek számával kerül kiszámításra.
A Shannon-formula (1) egybeesett a Boltzmann-formulával, amelyet 70 évvel korábban kaptunk az ideális gáz termodinamikai entrópiájának mérésére. Ez a kapcsolat az információmennyiség és a termodinamikai entrópia között a forró viták forrásaként szolgált, majd a számos tudományos probléma megoldásának kulcsa. A legáltalánosabb esetben az entrópiát értjük a rendellenesség mértékének, az anyagrendszer rendezetlenségének.
A termodinamika második törvényével összhangban zárt rendszereket, pl. rendszer megfosztotta attól a lehetőségtől, valós energia-információcsere a külső környezettel, keresik, és idővel elkerülhetetlenül jön a természetes stabil egyensúlyi belső állapot, amely megfelel az állam a maximális entrópia. A zárt rendszer hajlamos elemeinek homogenitására és az egymás közötti kötések energiájának eloszlására. Ie Információs folyamat hiányában az anyag spontán módon elfelejti a felhalmozott információt.
Már említettük, hogy a Hartley-képlet a Shannon-féle összetételű alternatívák formulájának speciális esete.
Az (1) képlet helyettesítve a pi helyett (az egyenlõtlen esetben az i) értéktől nem függõen. kapunk:
. Így a Hartley-képlet nagyon egyszerűnek tűnik:
Világosan jelzi, hogy minél nagyobb az alternatívák száma (N), annál nagyobb a bizonytalanság (H). Ezek a mennyiségek a (2) képletben nem lineárisan, hanem bináris logaritmussal kapcsolódnak. Logaritmus a 2. alapra és megadja az opciók számát az információmérési egységek - bitek számára.
Ne feledje, hogy az entrópia csak akkor lesz egész szám, ha N értéke 2, azaz. ha N a sorozathoz tartozik:
Ábra. 10. Az entropia függősége az egyenlőtlen választási lehetőségek számától (egyenértékű alternatívák).
Emlékezz rá, mi a logaritmus.
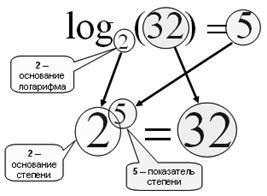
Ábra. 11. Az a alapú b logaritmus megkeresése egy erő megállapítása. amelyben szükséges a. hogy b.
Az alap-2 logaritmust binárisnak nevezik:
log2 (10) = 3,32 => 2,33 = 10
A 10 alap logaritmusa decimális:
log10 (100) = 2 => 10 2 = 100
A logaritmus fő tulajdonságai:
1. log (1) = 0, mert bármely nulla nulla teljesítmény 1;
Oldatok esetében inverz problémák, amikor ismert a bizonytalanság (H), vagy amelyeket annak eltávolítását mennyiségű információ (I), és szükség van annak meghatározására, hogy hány alternatívák egyaránt megfelel a megjelenését ez a bizonytalanság, az inverz képlet Hartley, ami még egyszerűbb:
Például, ha tudjuk, hogy ennek eredményeként a meghatározó, hogy mi érdekel Kohl Ivanov él, a második emeleten, ott kaptunk 3 bit információt, a szintek száma az épületben lehet meghatározni (3) általános N = március 2 = 8 emeleten.
Ha a kérdés: „az épület 8 emeleten, hogy mennyi információt meg kell tanulni, hogy mi érdekli Kolya Ivanov él a második emeleten?”, Akkor kell használni a (2) képlet: I = log2 (8) = 3 bit.