Személyes oldal - 13
13. A keresési, kiválasztási és válogatási algoritmusok.
A szekvenciális keresési algoritmus (APT) egymás után vizsgálja a lista egy elemét, kezdve az elsővel, amíg meg nem találja a célelemet. Feltételezzük, hogy a lista nincs rendezve.
A legrosszabb esetben: a célelem a lista utolsó eleme, vagy egyáltalán nem szerepel a listán.
Közepes eset: a keresés mindig sikeresen befejeződik, vagy néha a célérték nincs felsorolva.
A bináris keresési algoritmus (ADD):
A bináris keresés a rendezett listán történik. Az ötlet az, hogy a lista félig van felosztva, az átlagos el-t-t veszik és összehasonlítják a megcélzott el-tom-val. Összehasonlításkor három eredmény közül az egyik lehetséges: az értékek egyenlők, a célérték kisebb, mint a listaelem, vagy a célérték nagyobb, mint a listaelem. Az első, és a legjobb esetben az ügy befejeződött. A másik két esetben a lista felét le tudjuk dobni. Ha a célérték kisebb az átlagos elemnél, akkor tudjuk, hogy ha szerepel a listában, akkor ez a középső elem előtt áll. Ha ez több, mint az átlagos elem, tudjuk, hogy ha a listán van, ez a középső elem után van. Ez elég ahhoz, hogy a listának egy felét egyetlen összehasonlítással le tudjuk dobni. Ha ez az eljárás megismétlődik, akkor a lista fennmaradó részének felét eldobhatjuk.
A legrosszabb esetben a járatok száma k = log2 (N + 1).
Az átlagos A (N) ≈ log2 (N + 1) -1 eset
Néha szükségünk van egy e-mailre a listából, amelynek néhány speciális üzenete van, de nincs konkrét jelentése. Például az alkalmazottak listáján megtalálja az átlagéletkorot, vagy 5 munkatársat talál a legalacsonyabb fizetéssel. Általánosabb esetekben érdekelhetnénk az írásmódot a mező K-th legnagyobb értékével. Az ilyen rekord felfedezésének egyik módja a lista csökkenő sorrendbe rendezése; akkor a K. legnagyobb értékű rekord a K. helyre kerül. Ez sokkal több energiát igényel, mint a szükséges: az értékek, amelyek kevesebbek, mint amire keresünk, valójában nem érdekesek számunkra. A következő megközelítés hasznos lehet: megtaláljuk a legnagyobb értéket a listában, és a lista végén helyezünk el. Ezután megtaláljuk a legnagyobb értéket a lista többi részében, kivéve a már megtaláltat. Ennek eredményeképpen megkapjuk a lista második legnagyobb értékét, amelyet a listából a másodikra lehet elhelyezni. Ismételjük ezt az eljárást K-szor, megtaláljuk a K. legnagyobb értékét.
Az algoritmus minden egyes lépésénél kiválasztjuk az egyik bemeneti adatelemet, és beilleszti a már beállított listában a kívánt pozícióba, amíg a bemeneti adatok kimerülnek. A következő elem kiválasztása a forrás tömbből önkényes; szinte bármilyen választási algoritmust használhatunk. Általában (és egy stabil rendezési algoritmus elérése érdekében) az elemek beillesztésre kerülnek a megjelenés sorrendjébe a bemeneti tömbben. Az alábbi algoritmus ezt az adott kiválasztási stratégiát használja.
Bemenet: A tömb, amely A [1], A [2] elemekből áll. A [n]
míg j> 0 és A [j]> gomb:
Az algoritmus végrehajtási ideje a bemeneti adatoktól függ: minél nagyobb a szett rendezése, annál hosszabb a rendezés. A tömb kezdeti rendelése is befolyásolja a végrehajtási időt. Tehát a legjobb esetben a rendezett tömb, és a legrosszabb az a tömb, amely rendben van a rendezett sorrendben. A bemeneti adatok legrosszabb változatával rendelkező algoritmus időbeli bonyolultsága θ (n²).
Az algoritmus a rendezett tömbön átmenő ismétlésekből áll. Minden lépésnél az elemeket párhuzamosan egymással hasonlítjuk össze, és ha a páros sorrendje helytelen, az elemeket kicseréljük. A tömb mentén feltüntetett szakaszok addig ismétlődnek, amíg a következő lépés azt mutatja, hogy a cserék már nem szükségesek, ami azt jelenti, hogy a tömb sorrendben van. Amikor az algoritmus elhalad, egy olyan elem, amely nem a helyén van, "lebeg" a kívánt pozícióba, mint buborék a vízben, tehát az algoritmus neve.
A Shell rendezéskor először hasonlítsa össze és rendezze el azokat az értékeket, amelyek egymástól bizonyos távolságban d távolságra vannak. Miután ezt az eljárást megismételjük néhány kisebb értékei d, és a befejezett héj a fajta az elemek rendezését d = 1 (vagyis hagyományos beszúrási sort). Bizonyos esetekben a Shell válogatásának hatékonyságát az a tény garantálja, hogy az elemek "gyorsan" a helyére kerülnek.
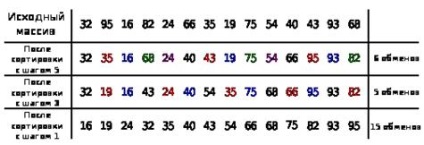
Egy példa. Adjuk meg az A = (32,95,16,82,24,66,35,19,75,54,40,43,93,68) listát, és sorba rendezzük a Shell módszerrel, és d értékeit választjuk 5,3 , 1.
Az első lépésben az összes A elemből álló A alosztályok, amelyek 5 pozícióval különböznek, azaz az A5,1 = (32,66,40), A5,2 = (95,35,43), A5,3 = ( 16, 19, 93), A5.4 = (82.75.68), A5.5 = (24.54).
A fogadott listában a második lépésben a 3 elemből elválasztott elemek alpontjai ismét sorba rendeződnek.
A folyamat az eredményül kapott lista betétlapjainak szokásos rendezésével végződik.
Az általános lista oszlopokra oszlik a kulcs rangja szerint. Minden egyes átjárónál a permutációkat a kulcs különálló értékének megfelelően végezzük. Minden egyes átvitel után a kötegeket egymásra rakják és egy másik kulcs kategóriába osztják.
Rekurzív rendezési algoritmus. Miután kiválasztott egy elemet a listán, a gyors sort két részre osztja. Az egyik részben az elemek kerülnek kiválasztásra, a másikban - kevésbé.
Olyan rendezési algoritmus, amely rendezi a listákat (vagy más olyan adatszerkezeteket, amelyekhez elemekhez való hozzáférés csak egymás után kapható, például - szálak) egy bizonyos sorrendben.
- Az osztható tömb két nagyjából azonos méretű részre tagolódik;
- Mindegyik kapott elem külön van rendezve, például - ugyanaz az algoritmus;
- Két rendezett félméretű tömböt egyesítenek.
A probléma kisebb méretűre történő rekurzív felosztása addig történik, amíg a tömb nagysága el nem éri az egységet (az 1-es hosszúság bármely sorrendje megrendelhetőnek tekinthető).