Inverz trigonometrikus funkciók
Bizonyos problémák a matematika és annak alkalmazása szükséges az ismert értékét trigonometrikus függvények, hogy megtalálja a megfelelő szög értéke kifejezett mértékben vagy radiánban. Ismeretes, hogy egy és ugyanazon érték a szinusz felel meg végtelen számú szögek, például, ha $ \ sin α = 1/2, $ szög $ α $ lehet egyenlő, és $ 30 ° $ és $ 150 °, $ vagy radiánban $ π / $ 6 és $ 5π / 6, és a $ bármelyike a szögek, amelyet úgy nyertünk, hogy a kifejezés a formában $ 360 ° ⋅k, $ vagy rendre $ 2πk, $, ahol $ k $ - bármilyen egész szám. Ez világossá válik a figyelmet a grafikon $ y = \ sin x $ a számegyenesen (lásd az ábrát $ 1 $ ..): Ha a tengely $ Oy $ elhalasztja szegmens hossza $ 1 / $ 2 és rajzol egy párhuzamos egyenes tengelye $ Ox akkor a szinuszot egy pont végtelen pontján metszik. A válaszok lehetséges változatosságának elkerülése érdekében inverz trigonometrikus függvényeket vezetnek be, más néven körkörös vagy ívfüggvényeket (a latin arcus-arc szóból).
Négy alapvető trigonometrikus függvények $ \ sin x, $ $ \ cos x, $ $ \ mathrm \, x $ és $ \ mathrm \, x $ megfelel a négy arkfunktsii $ \ arcsin x, $ $ \ ARccOS x, $ $ \ mathrm \ , x $ és $ \ mathrm \, x $ (olvasható: arcsine, arccosine, arctangent, arccotangent). Vegyük figyelembe az \ arcsin x és a \ mathrm \, x függvényeket, mivel a másik kettő az alábbi képletekkel fejezhető ki:
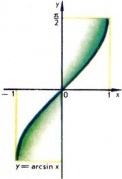
Egyenlet $ y = \ arcsin x $ eszközökkel definíció szögben $ y, $ radiánban és zárt tartományban $ - \ frac $, hogy $ \ frac, $ sine egyenlő $ x, $ azaz $ \ .. . sin y = x $ függvény $ \ arcsin x $ függvénye inverz függvény $ \ sin x, $ tekinteni az intervallum $ \ left [- \ frac + \ frac \ right], $, ahol ez a funkció monoton nő, és minden értéke $ -1 $ és $ 1 + $ egyértelmű, hogy az az érv, $ y $ funkciók $ \ arcsin x $ értékeket vehet csak az intervallum $ \ left [-1, + 1 \ right]. $ ez a függvény a $ y = \ arcsin x $ a szegmensben $ \ balra [-1, + 1 \ jobb], $ monoton módon növekszik, és értéke meg van töltve $ \ left [- \ frac, + \ frac \ right]. $ A függvény grafikája a 3. ábrán látható. $ 2. $
A $ \ -1 $ a \ $ a $ $ \ $ x = $ $ egyenlet összes megoldását az $ x = (-1) ^ n \ arcsin a + πn, $ n = 0, ± 1, ± 2, .... Például, ha
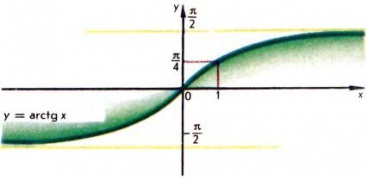
A $ y = \ mathrm \, x $ reláció minden $ x $ értékre definiálódik, és definíció szerint a $ y, $ radianumban kifejezett, $