Előadás rendezés
A rendezés az egyik legösszetettebb és legfontosabb tanulási algoritmus.
Először is, a válogatás számos számítógépes alkalmazás közös feladata. Gyakorlatilag minden lista értékesebb, ha egy bizonyos elv alapján rendezik.
Másodszor, sok rendezési algoritmus a programozás érdekes példái, amelyek fontos módszereket mutatnak: magánrendelés, rekurzió, listák kombinálása, bináris fák megtakarítása tömbökben.
Minden rendezési algoritmusnak előnyei és hátrányai vannak. A különböző algoritmusok teljesítménye az adattípustól, kezdeti helytől, mérettől és értékektől függ. Fontos kiválasztani az algoritmust, amely egy adott feladathoz legjobban megfelel.
A rendezés egyike azon kevés feladatoknak, amelyek pontos elméleti teljesítményhatárokkal rendelkeznek. Bármely rendezési algoritmus, amely összehasonlításokat használ, legalább O (N * logN) időt vesz igénybe.
Rendezés a választás szerint
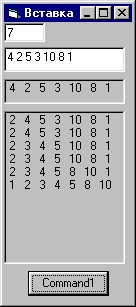
Válogatás szerinti választás egyszerű O (N 2) algoritmus. Feladata, hogy megkeresse a legkisebb elemet, amely az elemek elejétől kezdve a lista elejére vált. Ezután a fennmaradó elemek és a helyváltoztatások a második elemből származnak. A folyamat mindaddig folytatódik, amíg az összes elem el nem éri a végső pozícióját.
A legkisebb a7 = 1 elem van definiálva
Az első 1 4 5 3 10 8 2 helyek megváltoztatása
A többiek ismét keresik a minimális értéket és a második 1 2 5 3 10 8 4 változást
1 2 3 5 10 8 4 1 2 3 4 10 8 5 1 2 3 4 5 8 10 1 2 3 4 5 8 10
Ennek az algoritmusnak a végrehajtásához beágyazott For hurokra van szükség. A külső hurok (onI) a tömb elemek egymás utáni rögzítésére szolgál, belső (onJ) - a minimális (maximális) és pozícióját keresi. A belső hurok kilépése után az elemeket át kell alakítani. A külső ciklus utolsó elemét nem veszik figyelembe: ő maga fogja elfoglalni helyét.
Az i-edik legkisebb elem keresésekor az algoritmusnak ellenőriznie kell az N-megmaradt elemek mindegyikét. Az algoritmus végrehajtási ideje N + (N-1) + (N-2) + ... + 1 vagy O (N 2).
A választás szerinti választás jól működik olyan listákkal, ahol az elemek véletlenszerűen elrendezve vagy közvetlen sorrendben vannak, de a rendezett listák esetében ez az algoritmus teljesítménye valamivel rosszabb. A lista minimális elemének kereséséhez a kiválasztást a következő operátorok sorozata végzi el:
Ha a (j) Ha a listát sorrendben rendezzük el, az a (j) Ez nem a leggyorsabb algoritmus, de nagyon egyszerű, és gyorsan kicsi listákat rendez. A beszúrási rendezés egy másik O (N2) komplexitású algoritmus. Ez a részegység töredékének rendezett részében végrehajtott végrehajtáson alapul, ha megfelel a rendezési feltételnek. Az algoritmus növekvő sorrendben néz a forráslistára, és megkeresi azt a helyet, ahol új elemet szeretne beilleszteni. Ezután az új elemet a talált pozícióba helyezi. Az első lépésben a második elemet az elsőhöz, a másodikhoz - a harmadik elemhez hasonlítjuk össze az első és a második, és így tovább. Ha az ellenőrzött i + 1-es elem megfelel az elemek szerinti rendezési körülménynek, a sorrendbe zavarás nélkül beilleszti a j-os helyre. elemek indexekkel> = j és <=i-1 увеличивают свой индекс на 1. I = 2 és n 'összehasonlítást mindig kezdődik b = a (i): j = 1' az első Do Míg b> a (j) 'határozza meg a száma j = j + 1' behelyezésére hurok k = i-től j + 1 lépés: -1 'kiadott egy (k) = a (k - 1) „, ahol szúrni Következő ka (j) = b' hajtjuk inszertálására l = 1-től n Picture2.Print egy (L); ""; Következő Picture2.Print Következő I End Sub Az átmenetek teljes száma n-1. Az ilyen algoritmus rengeteg időt tölt, hogy megtalálja a megfelelő pozíciót egy új elemhez. Gyorsabb a választásnál. A buborék szortírozása olyan algoritmus, amely olyan rendezéseket tervez, amelyek már szinte rendezett állapotban vannak. Ha ez a feltétel teljesül, akkor az algoritmus nagyon gyorsan végrehajtódik, az O (N) sorrendben. Ha az elemek kezdetben tetszőleges sorrendben vannak elrendezve, az algoritmus végrehajtása (N2) lépésekben történik. A buborék válogatásával a listát szkennelni kell addig, amíg két szomszédos elem meg nem jelenik. Helyeket váltanak, és a listát tovább vizsgálják. Az első lépés után a legkisebb elem jelenik meg először (növekvő sorrendben). A következő lépés az elem megkezdése előtt történik, pl. a tömb többi része rendezve van. Az algoritmus megismétli ezt a folyamatot, amíg nem rendezi az összes elemet.Illessze be a válogatást
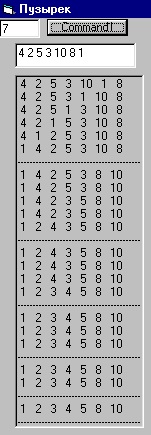
Bubble sorting

Piramis válogatás (bináris fák)
A piramis egy teljes bináris fa, amelyben minden csomó nagyobb, mint két gyermeke. Mindkét gyermekcsomónak kisebbnek kell lennie, mint a szülő csomópont, de bármelyikük nagyobb lehet a másiknál. A gyökércsomópont mindig a legnagyobb a piramisban.
Bármely tömbet piramisként ábrázolhatunk, ha a tömb első elemét a piramis gyökerébe helyezjük.
Például 2 4 5 3 10 8 1
A piramis egyik csomópontjából kiinduló alfa is piramis.
Ennek felhasználásával építhet egy piramist az alulról felfelé. A három csomóponthoz tartozó mindegyik részrészlethez piramist kell létrehozni. Ehhez össze kell hasonlítani a felső csomópontot a két gyermeke között. Ha a gyermekcsomópontok közül bármelyik nagyobb, akkor a felső csomóponthoz kell módosítania. Ha mindkét gyermekcsomó nagyobb, akkor a szülői csomópontról a gyermekcsomópontok nagyobbikjára kell váltania. Ezt a lépést addig ismételjük, amíg az összes alfa nem piramis:
Ezután nagyobb piramisok jönnek létre: a kis 10-es és 8-as csúcsú piramisokat összekapcsolják a 2. elemrel.
Ennek eredményeképpen a piramis legmagasabb pontja a szekvencia legnagyobb eleme. Mi dobjuk ki a piramisból, és helyére tegyük a legalacsonyabb elemet az alsó szinten. És újra piramist építünk. A tetején a következő legnagyobb elemet kapjuk, és így tovább.