Egységes forgalmazási jog
16. ábra - Az egyenletes eloszlás F (x) funkciója
Egy X véletlenszerű változó matematikai várakozása egy egységes jogszabályon keresztül [a. b], a mechanikai értelmezés (tömegközéppont) szerint, egyenlő a szakasz középső abszcisszal: M [X] = (a + b) / 2. Ugyanazt az eredményt lehet beszerezni és kiszámolni:
Az X véletlen változó varianciája a mechanikai értelmezésből is származik (tömegtörés pillanata a tömegközépponthoz képest): D [X] = (b - a) 2/12. Ugyanezt az eredményt kaphatjuk az integrál kiszámításával:
Egy egyenletesen elosztott véletlen változó átlag négyzetes eltérése
A módok nem egységesek; a szimmetriával kapcsolatos megfontolások mediánja (a + b) / 2. Ugyanezen szimmetriával kapcsolatos szempontokból az A [X] = 0 aszimmetria-együttható. Az X véletlen változó kurtózis-együtthatója -1,2: Ex [X] = -1,2; mint várható volt, negatív.
A rendszeres események várakozási ideje, például egy vonat várakozási ideje a metróban, egy bizonyos útvonali autóbusz várakozási ideje.
Tekintsünk néhány példát az egységes eloszlású véletlen változókra. Ha egy bizonyos értéket egy nagyméretű eszközzel mérünk, a kerekítési hibákat egy egységes törvény szerint osztjuk szét. Nyilvánvaló, hogy a számításokban az adatok kerekítéséből adódó hibák egyenletes eloszlást mutatnak.
17. példa A metróvonatok 4 percenként üzemelnek. Az utas bármikor érkezik a vonatplatformra. Keresse meg annak valószínűségét, hogy várni fogja a vonatot, hogy legfeljebb egy percet érjen el. Keresse meg a vonat átlagos várakozási idejét az utas által, számítsa ki a vonat várakozási idejének szórását és a várakozási idő szórását az utas által.
A megoldás. Vegyük figyelembe az X véletlen változót - az az idő, amikor az utas várja a vonatot. Valamennyi véletlen változó lehetséges értékei a [0; 4], és az állapot szerint mindezen értékek egyformán lehetségesek. Következésképpen a véletlen változó egy egységes törvény szerint osztódik szét az a = 0 és b = 4 paraméterekkel. Egy adott véletlen változó valószínűségi sűrűségfüggvénye:
Nézzük meg azt a valószínűséget, hogy az utas legfeljebb egy percet várni fog a vonatra:
A 17. ábrán a keltetésnél egy számot választunk ki, amelynek területe megegyezik a valószínűséggel
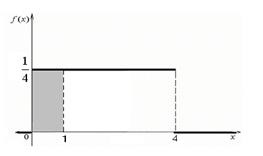
17. ábra - A valószínűségi eloszlási sűrűség grafikonja
Véletlen érték X - Várakozási idő az utasvonatra
Átlagos várakozási idő a vonat érkezésére az utas által