Bináris tömörítők
A tetszőleges igazságtáblázat alap-rendszerének végrehajtási elveivel összhangban, melyeket az előző fejezetekben figyelembe vettünk, megkapjuk a modulo 2 adder fő rendjét. A rendszer kialakítása nem különbözik a korábbi példáktól. Mint korábban, kiválaszthatunk olyan sorokat, amelyek egy kimeneti jelet tartalmaznak. Ezeket a "2I" elemekkel valósítják meg. A bemeneti jelek nulla potenciálját ezeken a vonalakban inverterek segítségével egyetlen egybe alakítják át. A logikai elemek kimenetének kombinálását a "2ILI" logikai elem végzi. A modulo 2 adder eredményezett áramköri ábráját a 15.1 ábrán mutatjuk be.
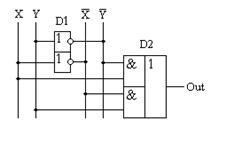
15.1 ábra - Az adder modulo 2 igazatábláját megvalósító vázlatos diagram
Az adder modul 2 (két bemenet esetén, áramköre teljesen egybeesik az exkluzív "OR" sémával) a kapcsolási rajzon látható, a 15.2. Ábrán látható módon.
15.2 ábra - Az "exkluzív VAGY" logikai funkciót ellátó áramkör feltételes grafikus kijelölése
A modulo 2 adder végrehajtja az összegzést anélkül, hogy figyelembe veszi a bináris számjegyek közötti átvitelet. Egy teljes bináris adderben figyelembe kell venni, ezért olyan elemekre van szükség, amelyek lehetővé teszik az átvitelt a következő bináris számjegyre. Az ilyen eszköznek, a félösszegzőnek nevezett igazatábláját a 15.2. Táblázat tartalmazza.
Megjegyezzük, hogy a fenti igazságtáblázatban lévő jelek az áramkörök számára elfogadott sorrendben vannak elrendezve, vagyis abban az értelemben, hogy a jel balról jobbra terjed. Ennek eredményeképpen jobbra van írva, hogy az összegzett számjegyek nagyobb bináris súlyúak. A matematikában a számjegyek eltérő sorrendjét fogadjuk el. A papír legmagasabb rangját a bal szélső számjegyre írja, a legalacsonyabb számjegy pedig az alacsony megbízást. Ennek eredményeként zavar keletkezhet. Ennek elkerülése érdekében megadom a félhitel igazatáblájának minden egyes sorának tizedesértékét (15.2. Táblázat).
Az igazságtábla első sorát a 0 + 0 = 010 (002) aritmetikai kifejezésből kapjuk. A második sor a 0 + 1 = 110 (012) aritmetikai kifejezésből származik. A harmadik sor az 1 + 0 = 110 (012) aritmetikai kifejezésből származik. A negyedik sor az 1 + 1 = 210 (102) aritmetikai kifejezésből származik.
15.2. Táblázat - A félhitel igazatáblája
Az önkényes igazságtáblázat felépítésének elveivel összhangban a félhitel vázlatos diagramját kapjuk. A 15.2. Táblázatban szereplő igazságtáblázatnak megfelelő sémát a 15.3. Ábra mutatja.
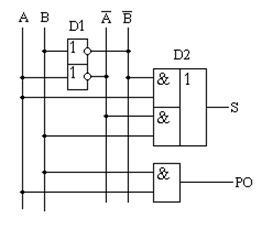
15.3 ábra - A fél eszköz hitelességi tábláját megvalósító digitális eszköz vázlata
A félig adókat különálló mikroáramkörök formájában adják ki, és különálló modulként használják a nagy integrált áramkörök szerkezetében, ezért a GOST biztosítja a féladagoló feltételes grafikus kijelölését. A 15.4 ábrán látható.
15.4 ábra - A féladagoló grafikus kijelölése
A fél-adder generálja az átvitelt a következő számjegyre, de nem veszi figyelembe az előző számjegyből történő átvitelt, így a fél-adder. Ennek a tulajdonságnak a következtében a fél-adagoló nem használható külön eszközként. A teljes összeadódás gyakorlati szempontból hasznos.
Egy teljes egybites bináris adder igazságtáblája (15.3. Táblázat), mint egy félösszegző igazságtáblája, beszerezhető a bináris számok számtani összegzésére vonatkozó szabályokból. A teljes összegző bemenetek és kimenetek kijelölésekor a következő szabályt alkalmazzuk: az egyjegyű bináris számokat A és B bemenetként használjuk; az összeg egy egyszámjegyű S bináris szám; az átadást P jelzi; az átvitel bemenetének jelzésére PI (I - rövid angol betűszó, bemenet) kombinációját használják; hogy az átvitel kimenetét PO (O-rövid, az angol szókibocsátás, a kimenet) kombinációjaként használják.
15.3 táblázat - Valódi bináris táblázat
Most, mint az előző esetekben, a tetszőleges igazságtáblázatot tartalmazó vázlatos diagram készítésének szabályai szerint egy teljes bináris egyszámjegyű sűrítő rendszert kapunk. A 14.3. Táblázatban szereplő igazságtáblázatnak megfelelő sémát a 15.5. Ábra mutatja. Ez a séma CDNF alkalmazásával készült.
15.5 ábra - Teljes bináris egyszámjegyű adder igaztáblázatát megvalósító vázlatos diagram
A teljes egybites összegző rendszere minimálisra csökkenthető. Ehhez elegendő megnézni az igazságtáblájának utolsó két sorait. Láthatjuk, hogy a hordozó jel nem függ a B bemeneti jeltől. Ezért ez a bemenet elhagyható az AND áramkör bemenetén.
A fenti érvelés eredményeképpen a két "3I" alsó elem helyett két 2-es "2I" elemet lehet használni. Pontosan ugyanaz a helyzet merül fel, ha figyelembe vesszük a 6. és a 8. sorokat. Ebben az esetben az A bemenet feleslegessé válik, azaz ebben az esetben egy két bemeneti "2I" logikai elemre lehet.
A PI bevitele felesleges a 4 és a 8 vonalakat ábrázoló kifejezésekben. A leírt műveletek eredményeképpen az adományozó következő számjegyére történő átvitelének vázlatos diagramja egyszerűsödik, és megkapja a 15.6 ábrán látható formát.
15.6 ábra - Minimalizált vázlatos diagram, amely egy teljes bináris egybites adder igazatábláját hajtja végre
Az egyszámjegyű bináris adder egy példája a beépített mikrokapcsoló K155IM1. A teljes bináris egyjegyű adder feltételes grafikus megnevezése a 15.7. Ábrán látható.
15.7 ábra - Teljes bináris egybites adder feltételes grafikus megjelenítése
Azonban a digitális jelfeldolgozó áramkörökben végzett számítások elvégzéséhez nem elegendő egy egybites adder pontossága. 16 vagy akár 40 bites bináris összeget használnak.
Annak érdekében, hogy a fenti egyszámjegyű többfunkciós készülék többszörös bitjét adja ki, elegendő a megfelelő bit fordítások bemenetének és kimenetének összekapcsolása. Négy egyjegyű adderrel végrehajtott négybites adder vázlatos rajza a 15.8. Ábrán látható.
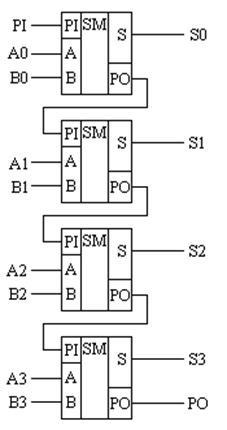
15.8 ábra - Négybites bináris adatfelvevő vázlata
A fenti séma szerint az A és B számok számjegyeinek bináris súlya közvetlenül a lánc nevéhez van hozzárendelve. Például az A0 áramkör az A szám nulla bitjét továbbítja, a B2 áramkör továbbítja a B szám második bitjét. A PI bemenet és a PO átvitel kimenete nem változik.
A teljes bináris négyjegyű additort ábrákon ábrázoljuk, a 15.9 ábrán látható feltételes grafikus jelöléssel. Megjegyezzük, hogy ebben a megjegyzésben az A bináris szó bemenetei egy külön mezőbe kapcsolódnak. Ugyanígy a bináris B bemenetek kombinálva vannak. A chip adott feltételes grafikus megnevezésén lévő átviteli jelek bemenete és kimenete külön mezőben is kiemelhető. Az így bemutatott chip sokkal jobban mutatja a funkcióit.
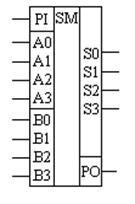
15.9 ábra - Egy teljes bináris 4 bites adder grafikus kijelölése az áramkörökön
A 15.8 ábrán bemutatott sémát nem optimalizálták a sebesség, hanem csak egy többbit bináris adder működésének elveit szolgálja ki. A gyakorlati sémákban soha nem lehetséges, hogy egymás után propagálják a szállítást a több bitű adder minden bitjén, mivel ez csökkenti a teljesítményét.
A bináris adder sebességének növelése érdekében minden bithez külön elválasztási sémát alkalmazunk. Az ilyen sémának az igazságtábláját könnyen beszerezhetjük az algoritmusból a bináris számok összegzéséhez, majd alkalmazzuk a digitális eszköz egy tetszőleges igazságtábláról való megépítésének jól ismert elveit.
A következő, amelyet a digitális jelfeldolgozó áramkörök széles körben használnak az eszköz által, digitális bináris multiplikátor. Ezeket az eszközöket mind a skálázási áramkörökben (erősítők vagy csillapítók), mind a heterodinizáló jelek, valamint a digitális szűrők részeként használják.