A Bernoulli-egyenlet
Távolítsunk el egy kis keresztmetszetű csövet egy állóáramú ideális folyadékból (39. Ábra). Tekintsük az áramlási cső falai által határolt folyadékmennyiséget, és az S1 és S2 szelvényekre merőleges irányban az áramvonalakat. Idővel Ez a térfogat az áramlási cső mentén mozog, és az S1 szakasz S'1 állásba mozdul el. az utat követve # 916; l1. Az S2 keresztmetszet az S'2 pozícióra mozdul el, az út mentén # 916; l2. A sugár folytonossága miatt az árnyékos mennyiségek ugyanolyan értékűek lesznek:
# 916; V1 = # 916; V2 = # 916; V.
A folyadék minden egyes részecske energiája a kinetikus energia és a potenciális energiából áll, a gravitációs erők területén. Az áramlás állóképessége miatt egy részecske idő után # 916; t bármely pontján az árnyékolt rész térfogata vizsgált (lásd, például egy O pont ábrán. 39.) azonos sebességgel (és ebből következően a kinetikus energia), amelyek egy részecske található ugyanazon a ponton a kezdeti időben időben. Ezért az energia növekedése # 916; E a teljes vizsgált térfogatból kiszámítható, mint az árnyékolt távtartók energiáinak különbsége # 916; V2 és # 916; V1.
Vesszük a jelenlegi cső és a szegmensek keresztmetszetét # 916; l olyan kicsi, hogy a v sebesség, a nyomás p és a h magasság egy és ugyanazon értéke hozzárendelhető az árnyékolt távtartók minden pontjához. Ezután az energiamegtakarítás az alábbiak szerint történik:
(# 961, a folyadék sűrűsége).
Az ideális folyadékban súrlódási erők hiányoznak. Ezért az energiamennyiségnek (98) meg kell egyeznie a kiválasztott erősségű munka által a nyomás erőkkel végrehajtott munkának. Az oldalfelületen lévő nyomóerők merőlegesek minden ponton azoknak a részecskéknek a mozgási irányára, amelyekhez hozzá vannak kötve, és ennek következtében semmilyen munkát nem végeznek. Csak az S1 és S2 szakaszokra alkalmazott erők munkája különbözik a nullától. Ez a munka
A (98) és (99) kifejezésekkel egyenlő, csökkentve # 916; V és az azonos mutatókkal egyenlő egyenrangúság egyik részébe való átvitelét kapjuk:
Az S1 és S2 szakaszokat teljesen önkényesen vették. Ezért azt lehet mondani, hogy minden része a cső jelenlegi kifejezésnek ugyanaz az értéke. Összhangban érintkező tett feltételezések származtatására egyenlet (100) lesz elég pontos csak hajlamos keresztmetszete S nullára, azaz. E. A kontrakciót csőáram a sorban. Így a p értékét, v és h, megjelenő bal és jobb oldalán az egyenlet (100) kell tekinteni tartozó tetszőleges két pontja egy és ugyanazon aktuális sor.
Az általunk nyert eredményeket az alábbiak szerint állíthatjuk elő: állóállapotú folyadék ideális folyadék bármely jelenlegi vonal mentén, állapot
A (101) egyenletet vagy az egyenértékű egyenletet (100) a Bernoulli-egyenletnek nevezzük. Annak ellenére, hogy ezt az egyenletet ideális folyadékhoz kaptuk, elég valósul meg valódi folyadékok esetén, ahol a belső súrlódás nem túl nagy.
Nézzünk néhány következményt a Bernoulli-egyenletből. Hagyja a folyadékáramot úgy, hogy a sebesség minden pontban ugyanolyan értékű legyen. Ezután, a (100) szerint, két tetszőleges pontra bármely áramvonalas,
amiből az következik, hogy ebben az esetben a nyomáseloszlás megegyezik a nyugalmi állapotban lévő folyadékkal [vö. (96)].
A horizontális áramvonalhoz a feltétel (100) a formát veszi fel
,
azaz a nyomás alacsonyabb azokon a pontokon, ahol a sebesség nagyobb (ez már kvalitatív módon szerepel az előző részben).
Bernoulli egyenletét alkalmazzuk a folyadék áramlásának esetére egy kis lyukon, széles nyitott edényben. Tüntessünk el egy folyadékban egy olyan folyadékcsövet, amelynek a szekciója egyrészt az edényben lévő folyadék nyitott felülete, másrészt a folyadék áramlásának nyílásán keresztül (40. ábra). Ezen szakaszok mindegyikénél a kiindulási szint fölötti sebesség és magasság azonosnak tekinthető, így számolni kell velük az e feltételezés alapján kapott (100) egyenletet. Ezenkívül mindkét szakaszban a nyomás atmoszferikus, és ezért azonos. Ezenkívül egy nyitott felület elmozdulási sebessége egy széles edényben nulla lehet. Mindezt figyelembe véve, a (100) egyenlet a formában írható
,
ahol v az átfolyási sebesség a lyukból. Vágás # 961; és h = h1 - h2 - a folyadék nyitott felületének magassága a lyuk felett, akkor:
,
Ezt a képletet Torricelli-képletnek nevezik.
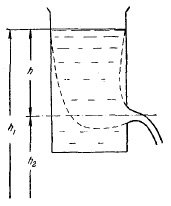
Folyadék, amely kilép a lyukból
Tehát a nyíláson levő nyíláson lévő folyadék kiáramlásának sebessége egy nyitott felület alatt h egybeesik azzal a sebességgel, amelyet bármely test megtalált, és h magasságból esik le.
Nem szabad elfelejteni, hogy ezt az eredményt azzal a feltételezéssel nyerjük, hogy a folyadék ideális. Valódi folyadékok esetén az áramlási sebesség kisebb lesz, és annál nagyobb az érték (102), annál nagyobb a folyadék viszkozitása.