Lineáris egyenletrendszerek vizsgálata
Vegyünk egy olyan m lineáris egyenleteket, amelyek ismeretlenek (1). Neki
Mivel a mátrix rangja lineárisan egyenlő a maximális számával
független sorokból (a mátrixban szereplő tételből), akkor a következő következtetést vonhatjuk le.
Ha a kiterjesztett mátrix sorai. és ezért az (1) rendszer egyenletei lineárisan függetlenek, akkor a mátrix rangja megegyezik egyenleteinek számával: r = m. ha lineárisan függenek, akkor r
A következő tételek két fontos kérdésre adnak választ:
1) Milyen esetben kompatibilis a rendszer (1)?
2) Ha a rendszer (1) kompatibilis, hány döntés születik?
Kronecker-Capelli tétel. A lineáris egyenletek rendszere csak akkor és csak akkor kompatibilis, ha a rendszer mátrixának rangja megegyezik e rendszer kiterjesztett mátrixának rangjával.
Egy közös rendszer esetében az r = r (A) = r () számot a rendszer rangsorának nevezzük.
A megoldások számáról szóló tétel. Adjuk meg a lineáris egyenletek közös rendszerének rangsorát. és az ismeretlenek száma a rendszerben n. Ha r = n. akkor a rendszer egyedülálló megoldást kínál; ha r
A rendszer (1) vizsgálatának eredményei egy áramkörben ábrázolhatók (2.
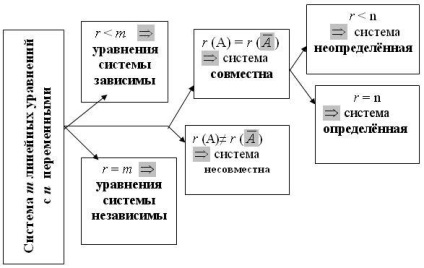
Ábra. 2 Lineáris egyenletrendszerek vizsgálata
Tegyük fel, hogy r
Az (1) rendszer megoldását, amelyben minden n-r nem alapváltozó nulla, az alapoldat.