Fény hullámelmélete
Fény hullámelmélete
Emlékezzünk arra, miért állítottuk le az optikai jelenségeket. Célunk volt egy másik, a korpuszkuláristól eltérő fényforrás bevezetése, ugyanakkor megpróbálva megmagyarázni a tények ugyanazt a területét. Ehhez meg kellett szakítanunk a történetet, és be kellett vezetnünk a hullámok fogalmát. Most visszatérhetünk témánkhoz. Az első olyan személy, aki teljesen új fényelméletet terjesztett elő, Newton kortárs, Huygens. A világosságról szóló értekezésében azt írta:
„Ha ezen túlmenően a fényt használ az áthaladás egy ideig -, hogy most fogjuk ellenőrizni, - ebből az következik, legyen egymás után időben, hogy ez a mozgás adódik át a környező ügyet; ezért, mint a hang, gömbölyű felületeken és hullámokon keresztül terjed; Úgy hívom őket a hullámok a hasonlóság, hogy azok a hullámok képződik a vízben, amikor műkő, ami egymás után bővülő körökben, bár a felmerülő különböző okok, és csak egy sima felületre. "
Huygens szerint a fény egy hullám, az energiaátadás, nem pedig az anyag. Láttuk, hogy a korpuszkuláris elmélet megmagyarázza a megfigyelt tények közül sokat. A hullámelmélet képes erre? Ismét meg kell kérdeznünk azokat a kérdéseket, amelyekre korpuszkuláris elmélet segítségével már válaszoltunk, hogy megnézzük, vajon a hullámelmélet ugyanolyan sikerrel tud-e válaszolni. Csináljuk itt a párbeszédes formában a H és D, ahol H - a beszélgetőpartner, győződve az igazságszolgáltatás a korpuszkuláris elmélet Newton, és a D - forrás győződve érvényességének Huygens elmélet. Sem egyik, sem a másik nem alkalmazhatja azokat a érveket, amelyeket a két nagy mester munkájának befejezése után nyertek.
H: A korpuszkuláris elméletben a fénysebességnek teljesen meghatározó jelentése van. Ez az a sebesség, amellyel a testek üres térben mozognak. Mit jelent a hullámelméletben?
G: Természetesen ez egy könnyű hullám sebességét jelenti. Mindenki tudja, hogy a hullám bizonyos sebességgel propagál, és ugyanaz a fény hullámainak kell lennie.
N: Nem olyan egyszerű, mint amilyennek hangzik. Hanghullámok terjednek a levegőben, a tenger hullámai - a vízben. Minden hullámnak rendelkeznie kell egy olyan anyaggal, amelyben propagál. De a fény áthalad a vákuumon, miközben a hang nem jár. Az üres térben lévő hullám feltételezése valójában azt jelenti, hogy egyáltalán nem vállalunk hullámot.
G: Igen, ez nehéz, bár nem új számomra. Tanítónő nagyon óvatosan tanulmányozta és úgy döntött, hogy az egyetlen módja annak, hogy egy hipotetikus anyagot, étert feltételezzen. amely közvetíti a teljes univerzumot. Az univerzum, úgymond, az éterbe merül. Ha bátran bátorítjuk ezt a koncepciót, akkor minden világossá válik.
N: De ezt a feltevést kifogásolom. Először új hipotetikus anyagot vezet be, és már túl sok anyag van a fizikában. Van egy másik ok is ellene. Nem kétséges, hogy mindent meg kell magyaráznunk, a mechanikán belül maradva. És mi van az éterrel? Képesek vagyunk válaszolni arra az egyszerű kérdésre, hogy az éter épül-e az elemi részecskékből és hogyan jelenik meg más jelenségekben?
G: Az első kifogásod természetesen tisztességes. De néhány mesterséges, súlytalan éter bevezetésével azonnal megszabadulunk sokkal több mesterséges könnyű szemcsétől. Csak egy "titokzatos" anyagunk van a végtelen számú helyett, amely a spektrum hatalmas számú színének felel meg. Nem gondolod, hogy ez valódi előrelépés? Legalábbis minden nehézség egy ponton koncentrálódik. Nincs szükségünk arra, hogy a különböző színű részecskék ugyanolyan sebességgel mozogjanak üres térben.
A második kifogás is igaz. Nem tudunk mechanikus magyarázatot adni az éterre. De kétségtelen, hogy az optikai és esetleg más jelenségek további vizsgálata feltárja szerkezetét. Jelenleg új kísérletekre és következtetésekre számíthatunk, de remélem, hogy végül képesek leszünk megoldani az éter mechanikai szerkezetének problémáját.
N: Egy darabig hagyjuk ezt a kérdést, mivel most nem lehet megoldani. Szeretném látni, hogy az elméletetek, még akkor is, ha nehézségekbe ütköznek, elmagyarázza azokat a jelenségeket, amelyek annyira világosak és érthetőek a korpuszkuláris elméletben. Vegyük például azt a tényt, hogy a fénysugarak vákuumban vagy levegőben haladnak egyenes vonalak mentén. Egy gyertya előtt elhelyezett papírlap tiszta és élesen árnyékolt árnyékot hoz létre a falon. Éles árnyékok nem lennének lehetségesek, ha a hullámelmélet helyes lenne, mert a hullámok a papír szélein megkerülnék, és így megpróbálták az árnyékot feltűnni. Egy kis hajó nem akadályozza a tengeri hullámokat, ahogy ön is tudja; csak körbejárják, és nem árnyékolnak.
G: Ez egy meggyőző érv. Vegyük a rövid hullámokat a folyón, egy nagy hajó oldalán. A hajó egyik oldalán megjelenő hullámok nem láthatók a másik oldalon. Ha a hullámok elég kicsiek, és a hajó elég nagy, nagyon tiszta árnyék jelenik meg. Nagyon is lehetséges, hogy a fény tűnik számunkra halad egyenes vonalban csak azért, mert a hullámhossza nagyon kicsi méretéhez képest a szokásos akadályok és lyukakat alkalmazunk a kísérletekben. Lehetséges, hogy ha elég kis akadályokat hozunk létre, akkor nem lenne árnyék. Nagy kísérleti nehézségekkel találkozhatunk olyan eszközök tervezésében, amelyek megmutathatják, hogy a fény elhúzza az akadályokat. Mindazonáltal, ha ilyen kísérletet lehetett végrehajtani, akkor döntő lenne a hullám és a fénysugaras világelmélet közötti küzdelemben.
H: A hullámelmélet a jövőben új tényekhez vezethet, de nem tudok olyan adatokról, amelyek meggyőzően megerősítik. Miközben bizonyossággal nem bizonyított, hogy a fény akadályozhatja az akadályokat, nem látok okot arra, hogy elhagyjam a korpuszkuláris elméletet, ami egyszerűbbnek tűnik számomra, és ezért jobb, mint a hullámelmélet.
Ezzel megszakíthatjuk a párbeszédet, annak ellenére, hogy ennek tárgya semmiképpen sem kimerült.
Meg kell mutatni, hogy a hullámelmélet hogyan magyarázza a fénytörést és a különböző színeket. Mint tudjuk, a korpuszkuláris elmélet képes ilyen magyarázatot adni. Elkezdjük a refrakciót, de először hasznos lesz egy olyan példát venni, amely semmi köze az optikához.
Hagyja, hogy két ember sétáljon a nagy nyitott téren, és szoros rudat tartva közöttük. Először egyenesen haladnak előre, ugyanolyan sebességgel. Míg a sebesség azonos, azok nagyok vagy kicsik - nem számít rúd elvégzi párhuzamos mozgás, azaz, hogy nem fog forogni, vagy változtassa meg irányát ... A rúd egymást követő pozíciói párhuzamosak egymással. De képzeljük el most, hogy egy nagyon rövid időre, talán egy másodperc törtrészeivel, mindkét ember mozgása egyenlőtlen. Mi fog történni? Nyilvánvaló, hogy ebben az időben a rúd el fog fordulni úgy, hogy az már nem mozog párhuzamosan eredeti helyzetével. Ismét folytatódik mozgást, azonos sebességgel, akkor azt eltérő irányban a kezdeti (ábra. 43) a változás irányát is bekövetkezik az időintervallum, amely a sebesség mind a gyalogosok változtattuk.
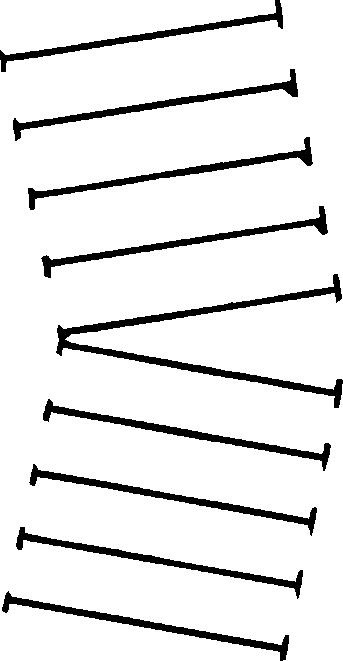
Ez a példa lehetővé teszi számunkra, hogy megértsük a hullám törését. Az éterben mozgó hullám síkja eléri az üveg felületét. Az 1. ábrán. 44 egy viszonylag széles elülső hullámot látunk, amely előre mozog. A hullám elülső része olyan sík, amelyben az éter minden része ugyanabban az állapotban van. Mivel a sebesség függ a médiumtól, amelyen keresztül a fény elhalad egy adott időben, az üvegben lévő sebesség eltér az üres tér sebességétől. Egy nagyon rövid időre, amire a hullám elülső része belép az üvegbe, a hullámfront különböző részeinek különböző sebessége lesz. Nyilvánvaló, hogy azok az alkatrészek, amelyek már elérték az üvegt, a fénysebességgel mozognak az üvegben, míg a többi rész még mindig az éterben a fény sebességében mozog. A meredekségi idő alatt a hullámfront mentén kialakuló sebességváltozás miatt a hullám iránya megváltozik.
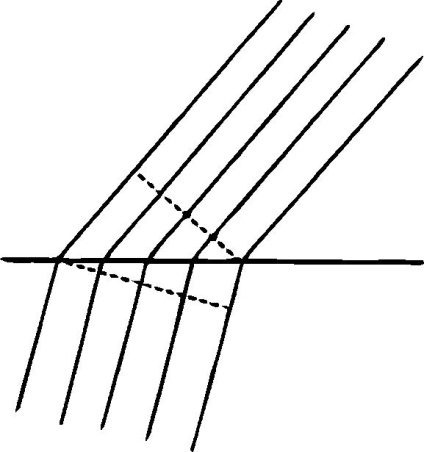
Tehát azt látjuk, hogy nem csak a korpuszkuláris, hanem a hullámelmélet is vezet a refrakció magyarázatához. A matematika további megfontolása és néhány alkalmazása azt mutatja, hogy a hullámelmélet magyarázata egyszerűbb és jobb, és ennek következményei teljes mértékben egyetértenek a megfigyeléssel. Valójában a kvantitatív analitikai módszerek lehetővé teszik számunkra, hogy a fénysebességet fénytörő közegen képzeljük, ha tudjuk, hogy a sugár megtörik mikor belép. A közvetlen mérések ragyogóan megerősítik ezeket a jóslatokat, és így a fény hullámelméletét is.
A színes kérdés továbbra is fennáll.
Nem szabad elfelejteni, hogy a hullámot két szám - sebesség és hullámhossz jellemzi. A fény hullámelméletének következő állítása nagyon fontos: a különböző hosszúságú hullámok különböző színeknek felelnek meg. A homogén sárga fény hullámhossza eltér a kék vagy az ibolya hullámhosszától. A különbözõ színekkel összefüggõ korpuszok mesterséges elválasztása helyett természetes hullámhossz különbséggel rendelkezünk.
Ebből következik, hogy Newton a fényszórással kapcsolatos kísérleteit két különböző nyelven írhatja le - a korpuszkuláris elmélet nyelve és a hullámelmélet nyelve. Például:
A különböző színekhez tartozó testcsövek vákuumban ugyanolyan sebességgel, de eltérő sebességgel vannak az üvegben.
A fehér fény a különböző színekkel kapcsolatos szemcsék gyűjteménye, míg a spektrumokban elválnak.
A különbözõ hullámhosszú, különbözõ színekhez tartozó sugarak ugyanolyan gyorsasággal rendelkeznek az éterben, de különbözõ sebességek az üvegben.
A fehér fény minden hosszú hullámhalmaz, míg a spektrumban elválasztottak.
Azt hiszem, nem lenne bölcs dolog elkerülni a kétértelműséget származó fennálló két eltérő elméletek ugyanaz a jelenség, úgy döntött, támogatja az egyikük alapos megfontolás után a előnyeiről és hátrányairól minden. Az N és G közötti párbeszéd azt mutatja, hogy ez nem egyszerű feladat. A döntés ebből a szempontból inkább az ízlés, mint a tudományos meggyőződés kérdése lenne. Newton idején és 100 évvel később a legtöbb fizikus inkább a korpuszkuláris elméletet.
A történelem sokkal később, a XIX. Század közepén ítélte meg a hullámelméletet és a korpuszkuláris elméletet. G-vel folytatott beszélgetése során kijelentette, hogy elvben lehetséges volt a két elmélet közötti vita kísérletileg megoldása. A korpusz elmélete nem teszi lehetővé a könnyű akadályokat, és világos árnyékokat igényel. A hullámelmélet szerint apró akadályok nem árnyékolnak. Jung és Fresnel munkáiban ezt az eredményt kísérleti úton szerezték; Elméleti következtetéseket is levontunk ott.
Már tárgyaltunk egy rendkívül egyszerű kísérletet, amelyben lyukkal ellátott képernyőt helyeztek egy fényforrás forrása előtt, és az árnyékot a falra dobták. A jövőben egyszerűsítjük a kísérletet, feltéve, hogy a forrás homogén fényt bocsát ki. A legjobb eredmény érdekében a fényforrásnak erősnek kell lennie. Képzeld el, hogy a képernyő nyílása kisebb és kisebb. Ha kap egy erős forrást, és képesek vagyunk, hogy egy lyuk elég kicsi, azt látjuk, új és meglepő jelenség, nem világos, hogy tekintve a korpuszkuláris elmélet. A fény és a sötétség között nincs éles különbség. A fény fokozatosan elhalványul, a sötét háttérbe átmenve egy sor könnyű és sötét gyűrűvel. A gyűrűk megjelenése nagyon jellemző a hullámelmélet számára. A világos és sötét sávok váltakozásának magyarázata egy kissé eltérő kísérleti beállítás esetén világos lesz. Tegyük fel, hogy van egy fekete papírlap, két tűs lyukkal, amelyeken keresztül fény áthaladhat. Ha a lyukakat szorosan egymás mellett helyezkednek el, és nagyon kicsi, és ha egyenletes fény elég erős, akkor a fal lesz a sok fény és sötét sávok fokozatosan gyengül, és fordult a sötét háttér előtt. A magyarázat nagyon egyszerű. Egy sötét zenekar jelenik meg, ahol az egyik lyuk hullám völgye találkozik a másik hullám hullámával, hogy mindkettő kialudjon. Fénysáv - ahol két medence vagy két lábon találkoznak a két lyukból érkező hullámok között, és megerősítik egymást. A korábbi példában szereplő sötét és könnyű gyűrűk magyarázata, amelyben egy lyukkal ellátott képernyőt alkalmaztunk, nehezebb, de elvben ugyanaz. Ez a megjelenése sötét és világos sávok, amikor a fény áthalad két hasíték, és a sötét és világos gyűrűk, amikor elhaladnak a lyukakat kell szem előtt tartani, mert később még visszatérünk, hogy a vita a két különböző kép. Az itt leírt kísérletek azt mutatják, diffrakciós fény - eltérés egyenes vonalú terjedési a fény, ha a fény útjába hullámok található kis nyílások vagy akadályok (ábra 45-47.).

Ábra. 45. A tetején látjuk a fényes foltok fényképeit, miután két sugarat két apró lyuk ment át egymás után (először egy rést nyitottunk meg, majd lezártuk, a másik pedig kinyílt). Az alábbiakban láthattuk azokat a sávokat, amelyeknek eredményeképpen a gerenda egyszerre haladt át mindkét kis lyukon (V. Arkadiev fotója)
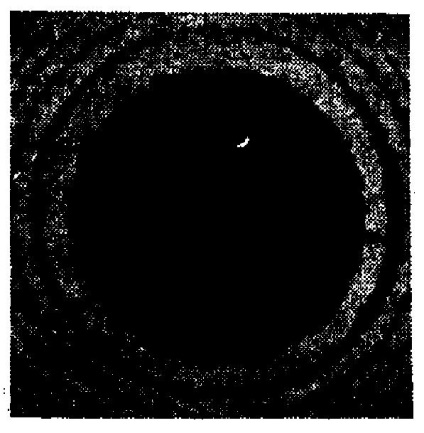
Ábra. 46. Fény fénydiffrakciója a gerenda körüli nagyon kis akadály következtében (Photo by V. Arkad'eva)

Ábra. 47. A fény átterjedése a sugár átvitelének eredményeképpen egy nagyon kis nyíláson keresztül (Photo by V. Arkadiev)
A matematika segítségével sokkal tovább tudunk menni. Meg lehet állapítani, hogy milyen nagy, vagy inkább, hogy milyen kicsi a hullámhossz, annak érdekében, hogy megteremtse a diffrakciós mintát. Így a leírt kísérletek lehetővé teszik számunkra az egyenletes fény hullámhossza meghatározását. Annak eldöntéséhez, hogy mennyire kicsi ezek a mennyiségek, megmutatjuk a látható napspektrum szélső sugarainak hullámhosszait, vagyis a piros és az ibolya sugarak hullámhosszát. A vörös fény hullámhossza 0,00008 cm, az ibolyaszín hullámhossza 0,00004 cm.
Nem szabad meglepődnünk, hogy ezek a mennyiségek nagyon kicsiek. A pontosan körülhatárolt árnyék, vagyis az egyenes vonalú fény terjedésének jelensége csak a természetben figyelhető meg, mert a szokásos lyukak és akadályok rendkívül nagyok a fény hullámhosszához képest. A hullám természete csak akkor észlelhető, ha nagyon kis lyukakat és akadályokat használnak.
De a fényelmélet keresésének története semmiképpen sem vége. A tizenkilencedik század ítélete nem volt végleges és végleges. A modern fizikusok számára a teljes választási probléma a korpuszok és a hullámok között újra létezik, most sokkal mélyebb és összetettebb formában. Fogadjuk el a korpuszkuláris fényelmélet vereségét, amíg nem találjuk, hogy a hullámelmélet gyõzelmének jellege problémás.
Ossza meg ezt az oldalt