A marcovite - stadopedia diverzifikációjának stratégiája
A stratégia középpontjában a portfólió hozamának kovariancia szintje áll. A befektető csökkenti a portfólió kockázatát azáltal, hogy a hozamot alacsony korrelációjú eszközök kombinációjával kezeli.
Hatékony portfólió Markowitz: a portfólió, amelynek kockázati szintje a legnagyobb, várható megtérülése. A modell a következő feltevéseken alapul: a befektető viselkedése:
- A döntést csak két paraméter befolyásolja: kockázat és jövedelmezőség;
- A befektető nincs veszélyben;
- Törekszik a maximális jövedelmezőségre meghatározott kockázati szint mellett;
- Ugyanazok a nézetek a várható hozamokról és kockázatokról;
- Mindenkinek közös befektetési horizontja van.
Egy eszköz készletének hatékony portfóliójához kiszámítjuk az n (n-1) / 2 változatok számát.
Ha a befektető kíván beruházni csak a kockázatos portfólió, ki kell választania egyet a portfoliók hatékony felderítő BC (lásd. Ábra. 2.1), amely megfelel a kockázat szintjét. Abban az esetben, a beruházás nélküli eszközök kockázati (eszköz Z, rf hozam) a hatékony felderítő kell választani csak egy portfólió, nevezetesen portfolió M. Megtalálható az érintők értékének kockázatmentes kamatláb rf a hatékony felderítő Markovtsev. A beruházó fogja választani portfolió M mivel hitelállománya álló eszközportfolió Z és M, ez lehetővé teszi a magasabb várható hozam az azonos kockázati szint, és a kockázatos portfóliók szegmensén helyezkedik hatékony BM határt. Így megalakult a hitelállomány változik a tényleges határ - ki van zárva a VM szegmensben, mint az új uralkodó portfóliók. Az effektív határt most az y / M vonal képviseli. Ez viszont azt jelenti, hogy abban az esetben, befektetés csak kockázatos eszközök, a befektetőnek választani portfóliók csak részben MS.
Tegyük fel, hogy a betétesek nem adható szabályt, és létrehoz egy listát az eszközök kockázata nélkül (Z) és a nagy kockázatú portfolió, de a kockázati portfólió úgy dönt, nem portfolió M9 és G. lista (lásd. Ábra. 2.2). Ezután a várt jövedelmezőség és kockázat lehetséges kombinációi az r / G. egyenes vonalon helyezkednek el.
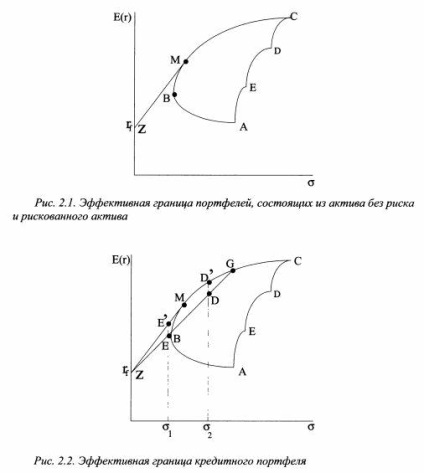
Amint az 1. ábrából látható. 2.2, ez a stratégia nem optimális, hiszen aktatáskák, határán helyezkedik r / MG, uralja a portfóliók a vonalon rf G (kivéve pont / y és G). Például, ha a befektető vállalja, hogy a kockázat a2, a portfolió D „uralja a portfolió a beruházó D. Ezért abba kell hagynia a választás csak kockázatos portfoliót D \ helyett kombinációja kockázatmentes eszköz és kockázatos portfólió G. Ha ő hajlandó kockázatot <УХ. то портфель Е' будет доминировать над портфелем Е. Чтобы получить портфель Е\ следует комбинировать актив без риска с рискованным портфелем Л/, а не G.
Így, ha a betétes egy hitelportfoliót szeretne létrehozni, akkor kockázatos portfólióként csak M. portfóliót kell választania.
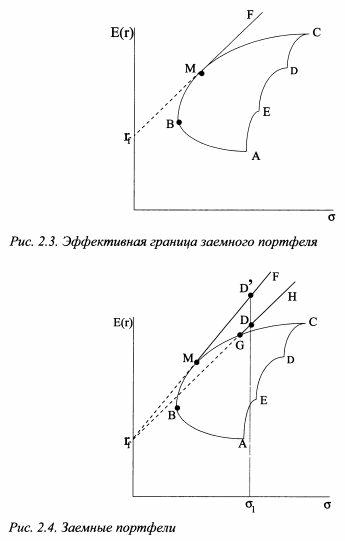
Tegyük fel, hogy a befektetőnek lehetősége van hitelportfólió létrehozására. Fogadja az alapokat a bet / y alatt, és kockázatos portfoliót szerez. Ezután minden lehetséges portfólió az MF vonalon található (lásd a 2.3. Ábrát), amelyet egy tömör vonal jelez. A kockázatos portfóliót úgy találjuk, hogy a ponttól / y-től az effektív határig érintő tangent rajzolunk. Tegyük fel, hogy a befektetői generál hitelállomány nem állományt megszerző A /, és egyéb kockázatos portfolió hatékony felderítő, mint portfolió G (lásd. Ábra. 2.4). Aztán kap hozzáférést bármilyen portfolió található egy egyenes vonal a GH, pl portfolió D. azonban ez a stratégia nem optimális, mert a nap a kockázati szint (<т,) можно получить более высокую ожидаемую доходность, купив портфель D\. Но для этого следует инвестировать заемные средства только в портфель M.
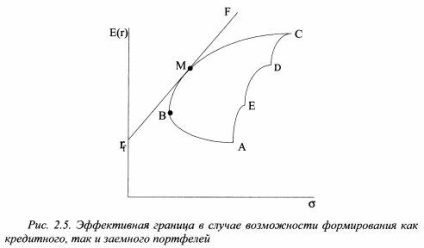
Így, ha egy befektető generálhat mind kölcsönzött és a hitelállomány, a kockázat az összes portfoliók hatékony felderítő, akkor válassza csak a M portfolió hatékony felderítő TFF viszont egy egyenes vonal (lásd. Ábra. 2.5).