A logikai elemek alapja
A logikai algebra szabályai lehetővé teszik, hogy egy logikai függvényt olyan formává alakítsunk át, amely logikai eszközként alkalmas a megvalósításra.
Például egy függvény
A funkció ebben a formában történő végrehajtásához két NE inverzort, három hárombemeneti 3I elemet, egy hárombemenetes 3If elemet:
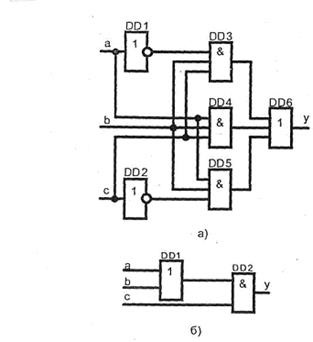
Az egyenértékű átalakulást a szabályok (6), (13), (19)
Nyilvánvaló, hogy az átalakulás után a 22 funkció sokkal egyszerűbb (23). A megvalósításhoz elegendő, ha egy két bemeneti elem 2I, egy két bemeneti elem 2ILI (b. Ábra). Mindkét séma (a, b ábra) lehetővé teszi egy és ugyanazon y függvény megvalósítását.
A logikai algebra törvényeinek figyelembe vételével csak három elemi függvényt használtunk (NEM, ÉS, VAGY). Összesen 4 függvény egy változó és 16 függvény két változó. Korábban megjegyezték, hogy az elemi funkciók segítségével bármilyen komplex logikai függvény létrehozható.
Definíció A funkcionálisan teljes rendszer (alap) logikai elemek gyűjteménye, amely lehetővé teszi bármely tetszőleges komplexitású logikai rendszer megvalósítását.
Bonyolult logikai függvény létrehozásához nem szükséges minden elemi funkciót használni. Engedélyezhető az elemi funkciók halmazának korlátozása, kivéve azokat az elemeket, amelyek mások által kifejezhetők. A függvények egymás után történő eltávolításával minimális bázist kapunk.
Definíció. Minimális alapon egy olyan funkciókészletet értünk, amely kizárja, hogy bármelyik függvény egy teljes rendszert egy hiányos rendszernévé alakítson.
Különböző bázisok lehetségesek, amelyek különböznek egymástól a benne foglalt funkciók számától és a funkciók formájától. Kiválasztása egy adott alapján készítettük logikai eszközök miatt milyen gazdaságosan kényelmes és egyszerű végrehajtani elemek műszakilag megvalósító függvények szerepelnek alapján, és minden logikai eszköz egészére.
Az inverzió (NOT), az (I), a diszjunktúra (OR) három logikai függvényében bármely elemi funkciót expresszálhat, és bármely komplex logikai eszközt létrehozhat. Három funkció (NEM, ÉS, VAGY) készlet alapja. Azonban az alap (NOT, AND, OR) nem minimális. Az egyik funkciót ki lehet zárni. A két függvény készletei (NEM, ÉS), valamint (NEM, VAGY) alapulnak. Valójában az AND függvény funkciókon keresztül valósítható meg (NEM, VAGY):
A VAGY funkció funkciókon keresztül valósítható meg (NEM, ÉS):
Korlátozás a bázisokra (NEM, ÉS); (NEM, VAGY) a kirekesztett művelet elvégzéséhez, három további NEM műveletet kell végrehajtania, ami gazdaságilag nem kivitelezhető. Ezért a gyakorlatban a három funkció (NEM, ÉS, OR) nem minimális alapját gyakran használják.
A chipeken nagyon praktikusan megvalósított logikai elemek kombinálják ezeket a funkciókat. A kényelem magyarázata az, hogy a tranzisztor inverzi a bemeneti jel fázisát, 180 ° -kal változtatja. Ezek az elemek AND-NOT (Sheffer stroke) és OR-NOT (nyíl Peirce).
Mindegyik elem (AND-NOT), (OR-NOT) egyénileg funkcionálisan teljes, lehetővé teszi tetszőlegesen összetett eszköz előállítását. Vegye figyelembe a NEM, ÉS, OR függvények végrehajtását (OR-NOT):
Az inverzióhoz mindkét bemenetre bemeneti jelet kell adni. A kötőszavakhoz először fordítsa meg a bemeneti jeleket, majd vigye be az OR-NOR műveletet. A diszjunktúra végrehajtásához hajtsa végre az OR-NOR műveletet, majd fordítsa meg az eredményt:
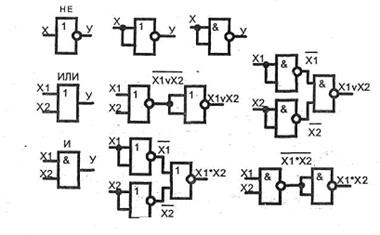
A (AND-NOT) alapon a NEM, ÉS, VAGY funkciókat az alábbiak szerint állítjuk be:
Látható, hogy a (24), (25) képlet hasonló. Az áramkörök megoldása a 3. ábrán látható.
A bázisok vonzereje egy logikai függvényből (AND-NOT) vagy (OR-NOT), hogy az egész logikai eszköz csak azonos logikai elemeken épül fel. Olyan logikai sémát kapunk, amely rendszeres szerkezettel rendelkezik. Csak ugyanazokat a logikai elemeket kell átköltöznünk. A logikai elemek (AND-NOT), (OR-NOT) alapjait széles körben használják az eszközök kialakításában, és nagy integrált áramkörökben megvalósíthatók. A nómenklatúra egy típusra való csökkentése megkönnyíti az eszközök tervezését. A bemeneteken lévő további inverterek javítják a terhelési kapacitást, és log-jeleket generálnak. 1 és a napló. 0 elegendő szintet.