A körvonal körül egy sokszöget ír le, keresse meg a kerületet - hogyan kell megoldani
A probléma leírása: Körülbelül olyan körből, amelynek R sugára R, olyan sokszöget írunk le, amelynek területe egyenlő S-vel. Keresse meg a kerületét.
A probléma része a USE-nek a 11. fokozatú alapszintű matematikához a 15. számon (tervezési problémák).
Nézzük meg, hogyan oldják meg ezeket a problémákat a példa felhasználásával, és általános megoldást találjanak.
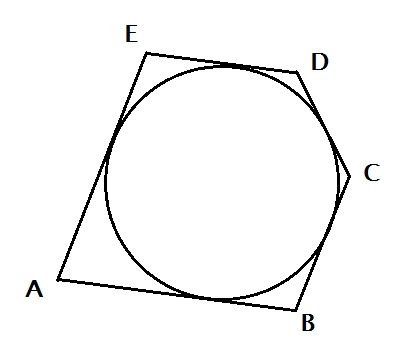
Egy olyan kör közelében, amelynek sugara 3, olyan sokszöget írunk le, amelynek területe 33. Keresse meg a kerületét.
A probléma megoldásához a kör közepét összekapcsoljuk a sokszög csúcsaival, és a háromszögek magasságát a poligon oldalára húzzuk.
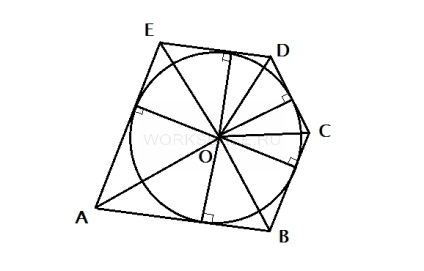
A sokszög területének megszerzéséhez mind az öt háromszög területét megkapjuk, és hozzáadjuk azokat. Ne feledje, hogy minden egyes háromszög magassága megegyezik a kör sugarával.
SABCDE = 1/2 ⋅ R ⋅ (AB + BC + CD + DE + EA)
Vegye figyelembe, hogy az összes oldal hosszának összege, vagyis a P perem zárójelben van, ezért a sokszögterületet a következő alakra alakíthatja:
SABCDE = 1/2 ⋅ R ⋅ P
Továbbra is helyettesíti a konkrét értékeket, és kifejezi a peremet:
P = 33/3 ⋅ 2 = 22
Így a poligon kerülete 22.
Általában a probléma megoldása a tervméretben a következő:
Egy poligon PERIMETER = 2 ⋅ S / R
ahol S a poligon területe, és R a benne írt kör sugara.
Csak a meghatározott értékek helyettesítésére és az eredmény kiszámítására marad.