A poligonok rendszeresek, félig szabályosak, csillagok

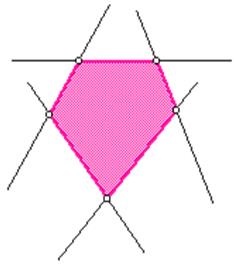
2 Konvex és nemkonverz poligonok A poligon konvexnek mondható, ha mindkét egyenes vonalán fekszik, amely két szomszédos csúcsa mentén halad.
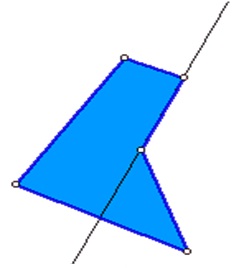
3 Konvex és nem konvektoros sokszögek A poligon nem konvexikus, ha van olyan vonala, amely az oldalát két részre osztja.
ha ($ ez-> show_pages_images $ page_num doc ['images_node_id'])
Konvex sokszögek tulajdonságai 1 0 A domború sík sokszögének két pontját összekötő szegmens (különösen bármelyik átlója) ebben a sokszögben található. 2 0 A domború sík sokszög háromszögekre oszlik minden csúcsának egyik (bármelyik) átlójából. 3 0 A konvex n-gon szögeinek összege 180 (n2).
5 Lapos sokszögek típusai
6 Konvex sokszögek típusai
7 Nem konvex sokszögek típusai
8 csillag-sokszögek típusai
9 típus sík poligonok

10 Szabályos sokszögek
11 Helyes sokszögek A konvex sokszögnek szabályosnak kell lennie, ha minden szög egyenlő és minden oldal egyenlő.
12 Pitagorák A rendszeres sokszögek tanítása a Pitagorasz-iskolában ered; Ráadásul a pythagoraiak úgy gondolták, hogy rendszeres sokszögek segítségével egy síkot fedeznek. A samosziak (Pythagoras of Samos) egy ősi görög filozófus és matematikus.

13 ARCHIMED A körkörös terület és a kör kerületének kiszámításához rendszeres feliratos és leírt sokszögek felépítését használtuk. Archimedes (BC) Ősi görög matematikus, fizikus, mérnök. ARCHIMED, amikor a megfelelő 96-gonnal dolgozott, levezette a π értékét.
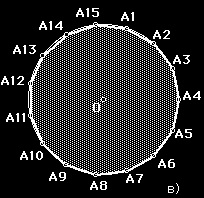

14 EVKLID Euclei (ie 300 körül) ókori görög matematikus. Először ismertette a rendszeres 3, 4, 5, 6-as konstrukciót, felépítette a megfelelő 15 gont.

16 AZ ÖRÖKSÉG SZERKEZET A gótikus stílus fejlődése és az ólomüveg széles körű használata a katedrálisok felépítésében szintén szükségessé vált a rendszeres sokszögek felépítésének problémáival való visszatéréshez.
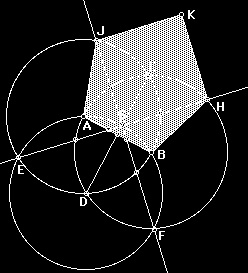

17 Albrecht DYURER- „Észak Leonardo” német művész Albrecht Dürer (r.) Végzett új építés egy szabályos ötszög, múló leszármazottai középkori út építésének végleges megoldást az iránytű.


18 ALBREHT DÜRER - "ÉSZAK-LEONARDO" A. Durer erődítményt folytatott, defenzív struktúrákat fejlesztett ki; megoldotta a rendszeres nyolcszög létrehozásának problémáját; kifejlesztette a művészileg végrehajtott betűk rajzolásának alapelveit.

19 nagy Leonardo da Vinci előadó és olasz tudós Leon CTA di Ser Pied nemzetségbe Bu nchi (Fa.) Bevonása konstrukciók, állítsa közötti arány az oldalsó és az n-szög apothem; Megfordult a figyelmet, hogy a fejlődés az első nyomtatás típusa; vonzotta figyelmét és díszeit.

20 Leonardo da Vinci barátja az olasz matematikus Luca Pacioli (r.) Leonardo mély érdeklődést az arányok létrehozott illusztrációk poliéderek, akiknek az arca szabályos sokszög.

22 KARL FRIDRICH GAUSS Biztosította a rendszeres 17-gon megépítésének lehetőségét. Ezt követően a 19 éves úgy döntött, hogy tanulmányozza a matematikát, nem pedig a filológiát.
23 Beírt és körülírt sokszögek A konvex sokszögnek egy körbe van írva, ha minden csúcsa ehhez a körhöz tartozik. A domború sokszöget körkörösnek nevezik, ha minden oldala megérinti ezt a kört.

24 A rendszeres sokszögek tulajdonságai 1 0 Egy szabályos sokszög van körkörösen fel van tüntetve és körülötte körülvéve, és ezeknek a köröknek a középpontjai egybeesnek. A rendszeres sokszög középpontja egybeesik a beírt és körülírt körök középpontjaival. 3 0 A szabályos n-gon oldalán az a = 2rsin 180 ° n képlet adja meg a körülírt kör R sugarát. 4 0 A rendszeres n-gonerek kerületét a körkörös körök sugarainak nevezzük.
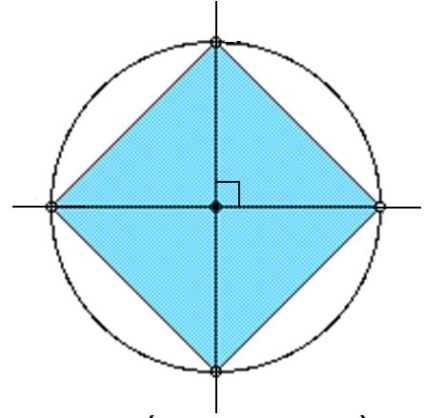
25 Szabályos sokszögek felépítése A jobb háromszög felépítése Szabályos hatszög létrehozása A jobb négyszög alakítása (négyzet)
26 Szabályos sokszögek felépítése Lehetséges bármilyen szabályos sokszög megépítése iránytűvel és vonalzóval? Ha rendszeres n-gont építettünk, akkor egy iránytűvel és egy vonalzóval használhatjuk a rendszeres 2n-gont. Például, ha a jobb háromszöget az iránytűvel és a vonalzóval megépítjük, egy iránytűvel és egy vonalzóval konstruálhatjuk a rendszeres 6-gon, 12-gon, 24-gon, 48-gont stb.
27 Szabályos sokszögek építése
28 A jobb sokszögek felépítése
29 A helyes szerkesztése Abban az esetben, ha egy szabályos sokszöget nem lehet egy iránytűvel és egy vonalzóval megépíteni, megközelítő konstrukciós módszereket használ (gyakorlati célokra). Például egy szabályos ötszög hozzávetőleges felépítése a következőképpen végezhető el: AD átmérő, AB = BC = CD; Az AMNKP a kívánt ötszög. sokszögek
31 PENTAGON Az amerikai katonai részleg épülete pentagram, és megkapta a "Pentagon" nevet, ami rendszeres ötszög.
32 Poligonális poligonok A következő konvex poligonokat félig rendszeres poligonoknak nevezzük: a) konformális poligonok, amelyekben az oldalak egyenlőek; b) egyenlő oldalúak, amelyeknél a szögek egyenlőek egyben.
33 Példák a félig szabályos sokszögekre Egyen-félig-spirális: ekvivalens-semireguláris:
34 Tulajdonságok semiregular sokszög 1 0 semiregular sokszög páros számú csúcsok a sokszög ravnougolnopolupravilnogo bárkinek lehet leírni egy kört, és akkor is csak az egyik bármely egyenlő oldalú semiregular sokszög kört lehet írva, és, sőt, csak egy ravnougolnopolupravilnogo átellenes oldalain egy sokszög párhuzamosak.

35 közül csillag sokszögek csillag sokszögek megkülönböztetni a jót és semiregular, ami viszont vannak osztva ravnougolnopolupravilnye és ravnostoronnepolupravilnye stellate sokszög.
36 Példák a rendszeres csillag alakú sokszögekre
37 Példák a félig szabályos csillag alakú sokszögekre Egyenetlen félkör alakú csillag alakú sokszög Egyenletes-félkör alakú csillag alakú sokszög
38. Épület a jobb csillag sokszögek Ha a felek szabályos n-szög, ahol n> 4, továbbra is keresztezi a kiterjesztése, másrészt, akkor kap a megfelelő csillag (önmagát metsző) n- gon. Egy példa az építőiparban a jobb csillag hatszög
39 Rendszeres sokszögek a természetben
40 Rendszeres sokszögek a természetben
41 Rendszeres sokszögek a természetben
42 Rendszeres sokszögek a természetben
43 Szabályos sokszögek parkettái

44 PENTAGRAM A legérdekesebb a tökéletes geometriai alak, az úgynevezett pentagram vagy pentacle. A Pentagram a pitagorai testvériség titkos jeleként szolgált, és az élet és egészség szimbólumaként választotta őket. A legenda szerint egy Pythagorean egy idegen földön megbetegedett, és halála előtt nem tudta fizetni a ház tulajdonosával, aki utánuk törődött. Az utóbbi egy csillag alakú ötszöget húzott házának falára. Miután látta ezt a jelet néhány évvel később, egy másik vándorló Pythagorean megkérdezte, mi történt a tulajdonosával és nagyvonalúan jutalmazta őt.
45 PENTAGRAM A Pentagram arányos, ezért gyönyörű. Nem véletlen, hogy ma az ötágú csillag a világ országainak majdnem fele zászlóin repül. Burkina Faso Venezuela Guinea-Bissau Görögország Vietnam Honduras Grenada Dzsibuti Dominika Zimbabwe Irak Jemen
46. Pentagram Kamerun Kína Comore Koreai Népi Dem-ik kerület - ka Kuba Libéria Mauritánia Mikronézia, Mozambik, Új-Zéland, Pakisztán, Pápua Új-Guinea Ilyen rendkívüli arányos szerkezete a pentagram, szépség eѐ belső matematikai tartalom az alapja eѐ külső szépség.
47. Jobb és csillag sokszögek művészeti Pattern „Star” minta „Daisy”
48. Jobb és csillag poligonok a mintát iparművészeti „nyolcágú csillag” minta „Pepita” minta „Sun” betét „Virág”


49 Pontos és csillag alakú sokszögek Udmurt művészeti és kézműves termékeiben
50 Pontos és csillag alakú poligonok Udmurt művészeti és kézműves termékekben

51. Jobb és csillag sokszögek udmurt termékek iparművészet
52 Köszönjük figyelmét!