A közvetlen prizmának egy elővágó sík általi építése autokad segítségével
Cél: megragadni a közvetlen prism keresztmetszetének valós értékét a síkcsere módszerével.
Tesztkérdések:
1. Milyen keresztmetszet a poliéder.
2. Melyik esetben a közvetlen prizmának a rajzból a további konstrukciók nélkül meghatározott vetülete?
1. feladat: a vetületi síkok cseréjével a prímszakasz valós értékét találja meg az elülső kiálló síkkal; a tárgyakat a vízszintes és az elülső síkra vetített vetületek adják (a feladatok változatait a B. függelék tartalmazza).
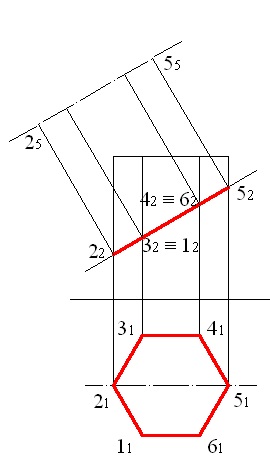
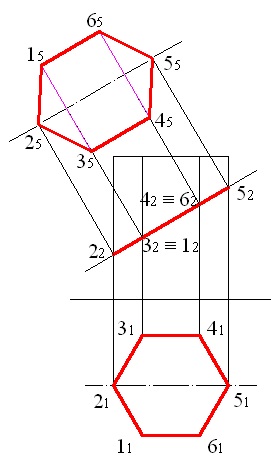
A problémát a vetületi síkok egyetlen cseréjével oldjuk meg. Az ábra egy hatszög keresztmetszetű, amit a rajzon az első síkja vetítési vonalszakasz és a vízszintes sík vetítési, mint a sokszög egybeesik a vízszintes vetülete a prizma (ábra. 5.1).
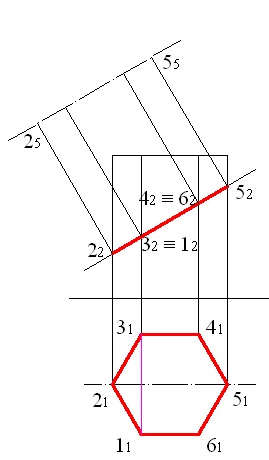
Ehhez tervezzük a szimmetria tengelyét egy további síkra
az OFFSET parancs segítségével rajzoljon egy szaggatott vonalat, amely párhuzamos a vágási sík első sávjával (5.2. ábra). A párhuzamos vonalak közötti távolság bármely lehet, ajánlott választani úgy, hogy az építkezés eredménye ne kerüljön a prizma elülső vetülete fölé.
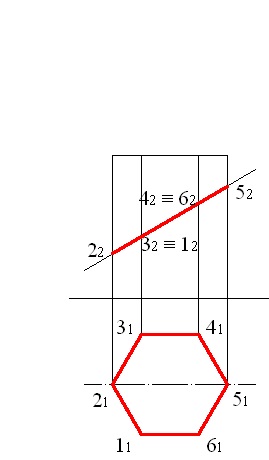
5.1 ábra - Egyenes hatszögletű prizma keresztmetszetének vetületei
5.2 ábra - A szimmetria-tengelynek egy további síkra való kivetítése
Most az 1-től 6-ig terjedő pontokat egy további síkra találjuk:
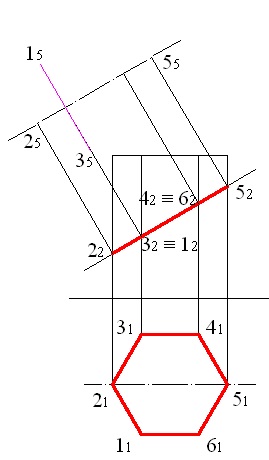
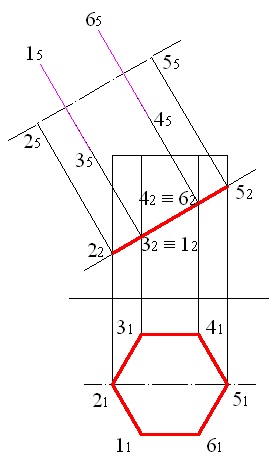
a szimmetriasík tengelyén a 22. 32. 42. és az 52. ábrán (2. ábra) merőlegeseket állítunk elő, ebben az esetben a 2. és 5. pontok nyúlványait kapjuk;
építésére vetítési pont 1, 3, 4 és 6, azt látjuk, a pontok közötti távolság 1 és 3, hogy csatlakoztassa a vízszintes vetületei ezeket a pontokat a szegmens (ábra. 5.4), a szegmens hossza egyenlő lesz a pontok közötti távolság, a párhuzamos a vízszintes síkkal;
5.3 ábra - A 2. és az 5. pontok kivetítése
5.4 ábra - Az 1. és 3. pont közötti távolság megkeresése
Az ALIGN parancs segítségével létrehozzuk az eredményül kapott szegmens vetületét a П5 síkra. Így a 15. és a 35. pont megtalálható (5.5. Ábra);
figyelembe véve, hogy ebben az esetben a 4 és 6 pontok közötti távolság egybeesik az 1 és 3 pontok közötti távolsággal, a kapott szegmenst másoljuk és a 45 és 65 pontokat kapjuk (5.6 ábra).
5.5. Ábra - Az 1. és 3. pontok kivetítéseinek elkészítése
5.6. Ábra - A 4. és 6. pontra vonatkozó kivetítések kialakítása
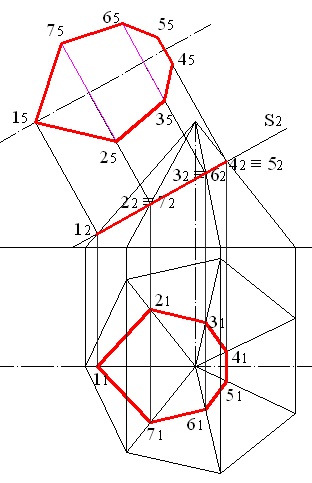
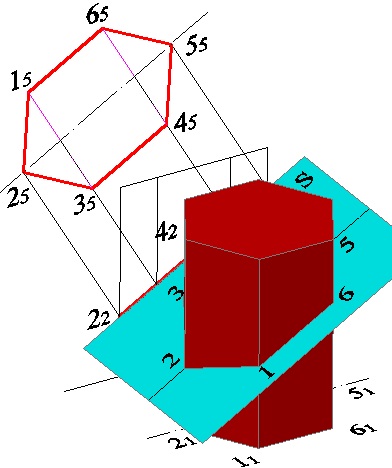
Mivel az AP5 sík párhuzamos a vágási síkkal, a 15. 25. 35. 45. és a 65. pontok a hatszög csúcsai, amelyek a keresztmetszet természetes értékei (5.7 ábra).
Az 5.8. Ábra bemutatja a szóban forgó konstrukció háromdimenziós modelljét.
Az 5.9. Ábra azt az esetet mutatja, amikor a secant sík áthalad a prizma felső bázisán.
Abban az esetben, ha a prizma alapja nem rendelkezik szimmetriatengellyel, akkor vonalat kell húzni a csúcs szélső szélétől jobbra vagy jobbra, majd mérni és rajzolni a távolságot a П5 síkhoz (5.10 ábra).
5.10 ábra - A szimmetria tengelyének hiánya
2. feladat: a kiugrások síkjainak cseréjével a piramisszakasz természetes értékét megtalálja az elülső kiálló síkkal; (a feladatok változatait a B. függelék tartalmazza).
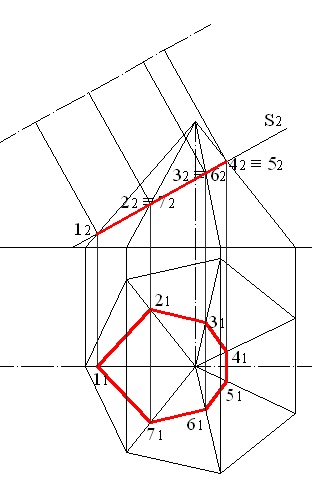
Tekintsük a heptagonális piramis szakaszának természetes értékét egy elülső kiálló síkkal. Az eredeti rajz az 1. ábrán látható. 5.11. A fentiekben ismertetett esetvel ellentétben a szakasz vízszintes vetülete nem egyezik meg az alap vetületével. Ezt a szélek metszéspontjainak homlokfelületeivel, a szekvenciasíkkal kell meghatározni, e pontok vízszintes vetületeit a levelezés határozza meg (5.12 ábra). A szakasz egy heptagon, csúcsa az 1., 2., 3., 4., 5., 6. és 7. pont.
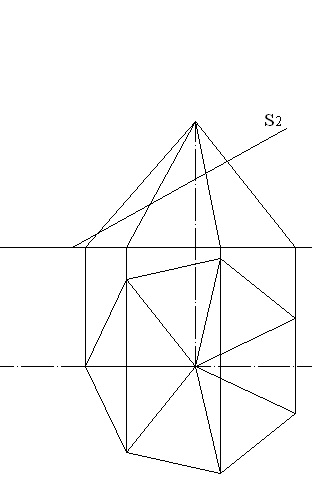
5.11 ábra - Piramis és szekvencia sík
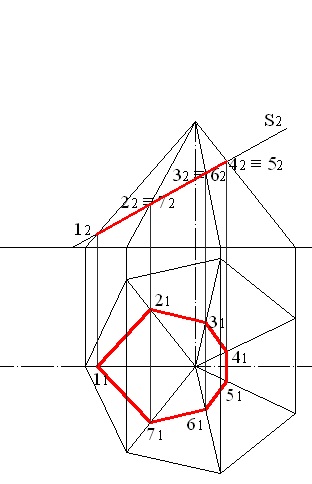
5.12 ábra - A piramisszakasz horizontális vetülete
A természetes keresztmetszeti érték megtalálásához az axiális vonal vetülete a szekcióval párhuzamos síkra épül. A merőlegeseket a szélek metszéspontjainak elülső nyúlványairól a szekvenciális síkra dobjuk (5.13. Ábra). A 2. és 7., 3. és 6., 4. és 5. pont közötti távolságot meghatározó szegmenseket építjük fel. Ezek a szegmensek párhuzamosak a vízszintes síkkal, így ezeket a fenti pontok vízszintes vetületei között megépítjük. Tervezzük a kapott szegmenseket a П5 síkra. A 15. és 25. pontok meghatározzák a 15. pontot. 25. 35. 45. 55. 65 és 75 a természetes keresztmetszeti érték (5.14. ábra).