Az azonosítható összetett objektumok ábrázolása relációs adatbázisban, nyitott rendszerekben
A kombináció a tárgy és relációs rendszerek aktívan tárgyalt a sajtóban - a különböző nézetek rendkívül Shiro, kezdve az ötlet alapvetően azonos adatokat modellek, ezt csak enyhe bővülése az egyiket, hogy a nyilvánvaló ellenzék, ami a következtetést, hogy lehetetlen az unió. A kritikát egyik vagy másik módon mindkét modellnek alávetik.
IT infrastruktúra az Ön vállalkozása számára
A kombináció a tárgy és relációs rendszerek aktívan tárgyalt a sajtóban - a különböző nézetek rendkívül Shiro, kezdve az ötlet alapvetően azonos adatokat modellek, ezt csak enyhe bővülése az egyiket, hogy a nyilvánvaló ellenzék, ami a következtetést, hogy lehetetlen az unió. A kritikát egyik vagy másik módon mindkét modellnek alávetik.
A részletek nélkül elmondható, hogy az egyes modellek hiányosságai elválaszthatatlanul kapcsolódnak előnyeikhez, és valójában ellentétesek egymással. Relációs rendszerek (R-rendszerek) kritizálták a rugalmasság hiánya, ami annak az eredménye a formális (és ezért a súlyossága és a stabilitás) és a tárgy (O-rendszer) - a hiánya formalitás, amely annak a következménye, a rugalmasság. [1.6.7,8, 19,21,22,23]
Ez a munka a relációs és tárgyi koncepciók gyakorlati teljességén alapul. Ennek a cikknek az a célja, hogy megmutassa, hogy ezek a fogalmak teljesen ellentmondanak egymásnak, és nem igényelnek változtatásokat ahhoz, hogy egy közös rendszerben használhassák mind az objektum, mind a relációs rendszerek tulajdonságait.
Ez az elgondolás a következő megállapításokon alapul:
- Ugyanazt az adatkészletet egyszerre több különböző modell írhatja le
- A relációs és az objektum modellek különböző modellek.
- A komplexitás szerkezete normalizálható.
Nézzük részletesen ezeket a kijelentéseket
Ugyanazt az adatkészletet egyidejűleg különböző modellek írhatják le
Mit értünk különböző adatmodellek alatt? Ezt az adatmodellek besorolásának szempontjából lehet figyelembe venni. Jelenleg az alkalmazott terület modellezés három szintjét különböztetjük meg: fogalmi, logikai és fizikai [18,20]. Ebben a példában kiválaszthatók a fogalmi szint (a C ++ objektummodellje) és a fizikai réteg (modell RAM) modellek. Így feltételezhető, hogy a különböző modellek különböző szintekhez kapcsolódnak. Az ilyen definíció azonban nagyon önkényes.
Szigorúan különböző adatmodellek nevezhetők ortogonális modelleknek. Az ortogonális modellek definíciója nagyon nem triviális. Ebben a cikkben érdekes az a következménye ortogonalitásának (azon a tényen alapul, hogy az adatok a modell lehet meghatározni, mint a beállított lehetséges adattípusok [2]): olyan adattípus határozza meg a modell M * ortogonális M modell lehet tekinteni az M modell csak a skalár (alap) típusú [6, 8, 10, 12, 13, 15]. A fenti példában a C ++ objektummodellben használt skalár típusok az alap típusok: int, char stb. Az adattároló elemek lehetséges típusainak leírása, pl. a RAM modellben meghatározott. Így azt mondhatjuk, hogy ugyanazt az adatkészletet egyidejűleg több ortogonális modell írhatja le.
Relációs és tárgyi modellek - különböző modellek
A relációs és tárgyi modellek az alkalmazási tartománymodellezés különböző szintjeire vonatkoznak. A relációs modell a modellezés logikai szintjére utal, az objektum modell fogalmi. Annak érdekében, hogy pontosabban meghatározzák a különbségeket a modellek között, fontolja meg az ezeken alapuló rendszereket.
Egy rendszert nevezhetünk olyan szabályszerűségeknek, amelyek meghatározzák a rendszer elemeinek létezését és kölcsönhatását. Egy bizonyos rendszer leírásához a következő műveleteket ismertetjük.
- Az ADR (X) művelet (ahol X a rendszer eleme) szükséges és elegendő a rendszer X elemének egyértelmű azonosításához. ADR (Xi)! = ADR (Xj) (Xi! = Xj) és ADR (Xi) = ADR (Xj) (Xi = Xj esetén). Az X elem egyértelmű azonosításához szükséges értéket adja vissza.
- Művelet (X) függvény az elem típusát X. Mivel a típus lehet meghatározni, mint a beállított attribútum nevek, akkor azt mondhatjuk, hogy a rendszerben van egy bizonyos sor az unió valamennyi készlet attribútum nevét minden fajta, amelyet a továbbiakban nevezzük a tér meghatározó típusok. Így az IS (X) művelet végrehajtja az X elemet a típusmeghatározási térbe.
Meg kell jegyeznünk, hogy általában az O-rendszer típusainak meghatározására szolgáló tér komplex és többdimenziós, ami a tipizálás különböző módozataiból következik [5,18] Az egyik ilyen módszer az öröklés. Ez a módszer csak az O-rendszerekben rejlik, és lehetővé teszi számunkra, hogy meglévő, általánosabb értelemben vett, alapvető típusokat használjunk az új típusok meghatározásakor. O-rendszerek örökségének köszönhetően ugyanaz a tulajdonság definiálható különböző típusokban. Az ábrán a B osztály az A osztály örököse, ezért az A osztályban definiált attribútumot a B. osztály-utódja is meghatározza. [1,5,16]
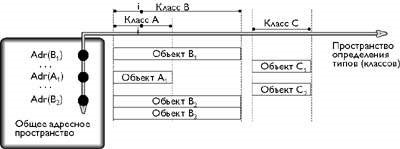
Ábra. 1. Az O-rendszer legegyszerűbb megvalósítása
Annak érdekében, hogy ábrázolja az R-űrrendszerekkel kell emlékezni klyuche.Eto koncepció kulcsfontosságú az R-rendszerek és a következőképpen definiáljuk: a legfontosabb kapcsolat egy részhalmaza halmazán belül az attribútumok nevei kapcsolat, amely hármas kapcsolat lehet egyedileg azonosítani értékeit a megfelelő attribútumokat ennek alcsoportok. Így a kulcs egy olyan értékkészletből áll, amely egyedileg azonosítja a táblázat bármely sorát. Egy bizonyos érték a kulcs mező (vagy mezők) tartozó rekord egy asztal, lehetővé teszi számunkra, hogy megtalálja ezt a bejegyzést a táblázatban. [1,4]
Egyedileg azonosítja a tuple R reláció X művelet ADR (X), vissza kell adnia kifejeződése formájában (R, K), amely úgy hangzik, mint a „K kulcsot tuple X R arány, ahol R = (x)». Ez a meghatározás egy idegen kulcs koncepcióján alapul, amelyet az O-rendszerek referenciáinak és mutatóinak R-analógjaként nevezhetünk. Meghatározása az ilyen jellegű bevezetését teszi lehetővé nem teszi lehetővé, hogy rendeljen egy linket (idegen kulcs) értékét adott ki a megfelelő arány az elsődleges kulcs értéket az R-rendszer (ábra. 2) egy olyan mechanizmus fenntartása a hivatkozási integritást.
Ha összehasonlítjuk az R- és O-rendszerek terét, két különbséget jegyezhetünk fel:
2. A típusmeghatározási térben: az 1. ábra örökölést szemléltet - az O-rendszerek egyik kulcsfogalmát. Az ábrán a B osztály az A osztály örököse.
Az R és O rendszerek kombináló rendszerének alapvető tulajdonságai külön-külön kell, hogy legyenek az egyes rendszerek mindegyikében rejlő tulajdonságokkal. ezért
- az ilyen rendszerben rendelkezésre álló összes adatot engedélyező struktúra tárgyává kell tenni.
- az ilyen rendszerben rendelkezésre álló összes adatnak relációs változók formájában kell megjelennie [9]
Ezek az érvek vezetnek bennünket a RecID-azonosító R-rendszerének bevezetéséhez, amely lehetővé teszi, hogy egyedileg határozzuk meg a rendszer bármelyik párját. Meg kell jegyeznünk, hogy a RecID-t tartalmazó mező bármelyik táblázat kulcsa, bár nem feltétlenül kulcsként definiálható.
A RecID bevezetése nem különösebben nehéz. A jelentés azonban nem magában a RecID-ben található. Fontos, hogy az értéket referenciák (vagy mutatók) inicializálására használják, amelyek lehetővé teszik a rendszer más részeinek hozzáférését ehhez a sorozathoz. Két esetet vizsgálhatunk:
Az örökség alkalmazása a kapcsolatokra
Nézzük meg ismét az (1) ábrán, amely leírja az O-rendszer térét. A B osztály az A osztály örököse. Így az IS (Bi) művelethez (ahol Bi a B osztály egyik objektuma) két lehetséges válasz helyes: az A és a B. osztály. Azt mondhatjuk, hogy IS (Bi) = IS (Aj) idő, mint IS (Ai)! = IS (Bj). Ez a minta az O-rendszerek rugalmasságának következménye az új típusok meghatározásának képességében.
Azonban, mivel különböző modellek egyidejűleg használhatók ugyanazon adatkészlet leírására, feltételezhető, hogy relációs és objektum modelleket lehet használni ehhez. Ehhez ezeket a modelleket ortogonálisnak kell tekinteni. És ahhoz, hogy ezeket a modelleket korrelálni tudjuk, erre emlékezünk
A komplexitás szerkezete normalizálható
Annak érdekében, hogy megértsük, mi értendő, térjünk vissza a példahez azzal a programmal, amely adatokat tárol a RAM-ban. Azt mondhatjuk, hogy minden információ RAM-ban tárolható (legalábbis eddig lehetséges volt). Ennek megfelelően információt modellezett objektum (itt azt feltételezzük, hogy minden programot, így vagy úgy egy eljárás modellezésére egy bizonyos domain) egy bizonyos memória elemek. Ami fontos, az a tény, hogy ez igaz minden program, hogy meg van írva a C, FORTRAN vagy szerelő (minden nyelv különböző programozási paradigmák és nem tiltakoznak) - minden esetben, akkor egy kis modellezett objektum társítva egy bizonyos memória elemek, az objektum adatait tárolja. Az előnye az objektum rendszerek, hogy azok lehetővé teszik csak kifejezetten meg a tárgy megfelel a szimulált területet azonosítható és értelmes (vagy, a másik, amelynek sajátos szerkezetét), egy sor memória elemek is (szempontjából G-rendszerek) nevezzük egy objektum.
Hasonló érvelés vonatkozik egy olyan objektumra is, amelynek adatait relációs adatbázisban kell tárolni. Abból a tényből, hogy az objektum egy tetszőleges belső szerkezetét információ tárolható egy relációs rendszer, ez szükséges ahhoz, hogy a következő következtetés: minden olyan tárgy is társítható azonosítható és értelmezhető sor sorok.
Tekintsük ezt a rendelkezést részekre:
1) az objektum egy azonosítható sorozata. Az objektumokkal kapcsolatos adatokat tartalmazó csoportok egy olyan egyedi azonosítóval társíthatók, amely valójában egy objektumazonosító (OID), amellyel egy adott sorcsoportra hivatkozhatunk;
2) az objektum egy értelmes sorcsoport. Az objektumot egy típus írja le, amelynek minden attribútumához egy bizonyos szemantikai értéket helyezek levelezésre. Ez a szemantikai érték határozza meg az objektumban lévő tuple jelentését, és ezenkívül az objektum attribútumához hozzáférést biztosít ehhez a sorozathoz.
Nagyon fontos megérteni, hogy itt az a pont, amely a tárgyak jellemzőjeként rejlik a zsidóságban. Az a tény, hogy bármelyik párkának van saját jelentése, és ezt a jelentést az a vezénylet határozza meg, amelyben ez a zsűri belép. A tuple maga semantikus értelemben vett adatkészlet. És ez az értelmes adatkészlet szintén értelmes az objektum kontextusában, amelynek egy attribútum. Ebben nincs ellentmondás. Tekintsük a következő példát.
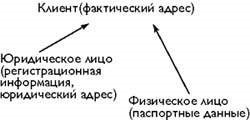
Példánkban osztályokkal (tárgymodell) és kapcsolatokkal (relációs modell) foglalkozunk. Mivel az objektum és a relációs modellek csak ortogonálisnak tekinthetők, ezt a példát az alábbiak szemléltetik (4. ábra)
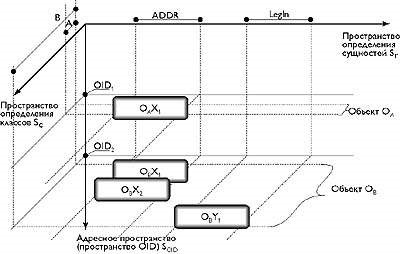
Ábra. 4. R * O-rendszer