A tanórákon kívüli tevékenység vizuális geometriában a 7. fokozatú "olló geometriájában
"Az olló geometriája. A vágási és hajtogatási adatokkal kapcsolatos feladatok »
A szövetségi állami oktatási előírások első helyen állnak, nem objektív, hanem személyes eredmény. Nem annyira maga a tudás, mint előtérbe kerül, mint a független beszerzés eszközei és eszközei, a tudás elmélyítése és frissítése, függetlenül attól, hogy melyik tartományhoz tartoznak.
Egy tanár számára a szövetségi állami oktatási normákra való áttérés átmenet a tudás átadásától az aktív tanulás feltételeinek megteremtéséhez és a gyermekek gyakorlati tapasztalatainak megszerzéséhez.
A hallgatók számára ez az átmenet az információ passzív asszimilációjától aktív keresésig, kritikai gondolkodásig, a gyakorlatban való felhasználásig.
Nehéz nem ért egyet azzal, hogy a geometriai problémák mindig a legnagyobb nehézségeket okozzák a diákoknak. Ennek eredményeképpen sok diplomás rosszul oldja meg a "Geometria" modul feladatait a végső minősítésen. Véleményem szerint sok oka van ennek a szubjektívnek és objektívnek. Íme néhány közülük: gyenge belső (kognitív) motiváció, az érdeklődés hiánya megoldásában geometriai problémák, a képtelenség, hogy biztosítsák a legfontosabb dolog a probléma gyengén fejlett térbeli képzelőerő, a megértés hiánya a kapcsolat a megszerzett tudás, készségek és azok gyakorlati alkalmazása, stb azt hiszem. Az ilyen feladatok megoldásában sok segítséget nyújt az építési feladatok. Ezek a feladatok általában nem teszik lehetővé számukra a szokásos megközelítést és a hallgatók számára való formális felfogást. Ezek a célok azonban az iskolai geometria során kapott kevés időt és figyelmet, a végén minden jön le csak úgy a legegyszerűbb műszaki problémák, bár a fontosságát konstruktív feladatokat a fejlesztés logikus gondolkodás, esztétikai nevelés és alkalmazott orientáció nem lehet túlbecsülni. Ezek a problémák hasznosak a térbeli látás fejlesztésében is, ami a felsőbb osztályokban a sztereometria tanulmányozásához szükséges.
Ezért egyszerűen meg kell vizsgálni az építési feladatokat a tanórán kívüli tevékenységekben, és minden bizonnyal hozzá kell adni a vágási és összecsukható számadatokat, valamint a kockás papírra vonatkozó feladatokat. Még ezek a látszólag egyszerű feladat hozott diplomások patthelyzet, hiszen nem a saját módszereit problémák megoldására, hiányzik belőlük a kialakított geometriai ábrázolása területet és annak tulajdonságait. Kihívások a vágás és a hajtogatás kockás papírra célkitűzések célja ezen hiányosságok kijavításának, továbbá azok a készségek fejlesztése, növelése érdeklődés geometria és a matematika, fejlesztésére képzelet, a logika, a forma és fejleszteni a kutatási képességek.
Példát adok az egyik geometriai extracurricular osztályba, amelyet a 7. évfolyamon tartottak.
- különböző feladatokkal rendelkező diákok ismerete a vágási és hajtogatási adatok tekintetében;
- a kockás papírra vonatkozó számok feltérképezése;
- a diákok térbeli képzeletének kialakulása;
- a hallgatók keresési és kognitív aktivitásának aktiválása;
- mérlegelni kell a geometriai problémák megoldásának különböző módjait a sík síkbeli ábrázolására és összecsukására;
- ismerkedjen meg a kockás papír feladataival és megoldásaival;
- A diákok leleményességének és nem szokványos gondolkodásának fejlesztése;
- érdeklődés kialakítása a tudás gyakorlati felhasználásában a tervezésben.
Nézd meg a híres és ismeretlen művészek képeit. Mit gondolsz, mi egyesíti őket?






Próbálj fantáziálni és kitalálni, hogy milyen feladatokkal lehet a képek karaktereit elfoglalni? Lehetséges, hogy megoldják az építési problémát. És mi ismerjük ezeket a feladatokat? Milyen eszközöket használhatok klasszikus építési feladatok megoldására?
De ma számos egyéb problémát megoldunk. És mi ezek a feladatok, találd magadnak. Ismeretes, hogy ezekkel a feladatokkal látszólag egy primitív emberrel szembesült, amikor megpróbált vágni egy halott vadállat bőrét, hogy saját ruháit varrja. Sok hasonló hasonló probléma megoldását az ókori görögök találhatják. Arra gondoltam, hogy milyen problémákról beszélünk?
Igen, természetesen a vágás feladatairól beszélünk. A számok kivágásának vagy átalakításának feladatai a szélsőséges ókorban jelentek meg. Már a 7.-19. században. BC Indiában a "kötél szabályai" című könyvet a két négyzetből álló alak átformálásával, egy négyzetével megegyező négyzetes négyzet alakításával kezeljük. A hasonló problémákkal rendelkező első írásos forrás a 10. századból származik - ezek az Abul-Weh perzsa csillagász fragmensei, akik Bagdadban éltek. A professzionális matematikusok komolyan foglalkoztak a XIX.
Tegye félre az iránytűket, és vegye az ollót. Vágás, vágás, gondolkodás - ez az, ami megoldja az ollók geometriai problémáit.
A számok vágásához és átformálásához szükséges feladatok.
Szerkessze át az ábrát, amely két négyzetből áll.
(A probléma megoldásához a fiúknak meg kell találniuk a választ a kérdésre: mely számok egyenlőek? Megtalálják a választ akár a matematikai referenciakönyvben, akár az interneten).
A megoldás. Vágjon át minden négyzetet átlósan. Az átlósok lesznek a létrehozott négyzet oldalai.
Vágja ki a téglalapot, amelynek hossza 9 cellás, és a szélesség 4, két egyenlő részre, így hozzáadhat egy négyzetet tőlük.
Építsen egy téglalapot 2 cm és 5 cm-es oldalakkal, vágja át a téglalapot átlósan. Adja hozzá a háromszöget a kapott részekből.
Lehetséges-e egy másik háromszög hozzáadását ezekből a részekből, amely nem egyenlő ezzel? Ha lehetséges, hajtson még egy háromszöget.
Hozzon létre egy téglalap alakú háromszöget, amelynek két oldala egyenlő. Vágjuk három egyenlőtlen részre, ahonnan két egyenlő négyzetet készíthet.
Vágja a négyzetet 3 darabra, ahonnan 3 éles szögből és három különböző oldalról háromszöget hajthat.
Az oldat az ábrán látható.
Feladatok a kockás papírra vonatkozó szám megtalálásához.
A diplomások átadják az USE-t, amely magában foglalja érdekes, nem szabványos problémák megoldását a geometriai folyamat során. Sokan közülük megoldások nélkül is megoldható, de a vágás és átalakítás módszerével. Tekintsünk egy ilyen problémára.
5. feladat. Keresse meg a trapéz területét egy kockás papírra 1 cm × 1 cm méretű cellával (lásd az ábrát). A válasz négyzetes centiméterben ad.
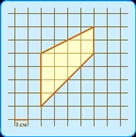
A srácok először kínálják megoldásaikat.
És most javaslom, hogy fontolja meg az egyik megoldást. Nem ismered a képletet a trapéz területének megtalálásához, de jó képzelőerővel. A módszer hasonlít egy puzzle megoldására - hogyan lehet egy lapos alakot részekre vágni, hogy ezekből a részekből, ha mindegyiket ugyanannyi alkalommal használják, téglalapot hajtanak? Ezután számold meg a téglalapon belüli cellák számát, és oszd meg az adott alak részleteinek ismétléseinek számával. Lásd.
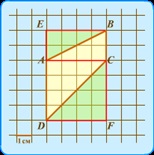
Újabb AC vonalat rajzolunk, és a trapéz két részre "vágjuk", ahogy a megoldásnál a második módon. További vonalakat rajzolunk, és az E és F csúcsokat felépítjük, mint a megoldásnál a harmadik módon. Meggyőződésünk, hogy az eredményül kapott zöld és sárga háromszögek páronként egyenlők (a megfelelő oldalakon lévő sejtek számítása). Így, hogy egy téglalapot építsenek, az adott ábra részleteit kétszer használták fel, egy sor sárga, a második pedig zöld. Számítjuk a töltött téglalap összes celláját. 24. 24. 2 = 24/2 = 12. Válasz: 12.
Tekintsünk még egy megoldást a probléma megoldására. A módszer ugyanazt a tudást igényli, mint az előző, csak kicsit másképp néz ki a képen. Most nem "vágjuk" a trapéz részeit, hanem "kivágjuk" egy téglalapból, amelynek oldala az adott trapéz csúcsain keresztül a rácsvonalakon halad át.
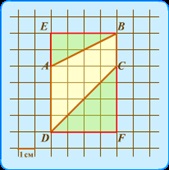
A vízszintes vonalakat a B és D csúcsokon keresztül húzzuk, folytassuk az AD és BC függőleges vonalakat a vízszintes vonalak metszéspontjához. szimbólumok jelölik metszéspontok E és F. kapott DEBF téglalap oldalai DE = 6 és DF = 4, területe 6 × 4 = 24. Annak érdekében, hogy a kívánt terület a trapéz, szükséges a terület a téglalap kivonó terület (zöld) AEB és DFC háromszögek.
SAEB = AE · EB / 2 = 2 · 4/2 = 4 és SDFC = DF · FC / 2 = 4 · 4/2 = 8.
Következésképpen a trapéz területének területe S = 24 - 4 - 8 = 12.
Tekintse meg a feladatokat az USE feladatok nyílt bankjából, javasoljon megoldásokat.




Kalandunk véget ér. A következő leckében továbbra is a problémák megoldását, a vágás, átalakítása, a megállapítás területek számok beosztású papíron, adjunk hozzá néhány számok a koordináta síkon. Remélem, hogy a vizuális geometria világa lenyűgözött.
Javaslom, hogy a következő lecke egyikének egyikét végezze el:
- az USE matematikai feladatok nyitott bankján lévő problémák kiválasztása és megoldása a kockás papíron ábrázolt területek megtalálásához.