A geometriai testek rajzai és axonometrikus vetületei - rx-fly Mindent tanulmányozok itt!

11. A geometriai testek rajzai és axonometrikus vetületei
Tehát már tudod, hogy a legtöbb tárgy alakja különböző geometriai testek vagy azok részei kombinációja. Ezért az olvasáshoz és a rajzoláshoz tudnia kell, hogyan képviselik a geometriai testeket.
11.1. Egy kocka és egy négyszögletes párhuzamos tüskék kivetítése. A kocka úgy van elhelyezve, hogy az arcai párhuzamosak a vetületek síkjával. Aztán megjelenítés azok párhuzamos síkokban vetületei egy életnagyságú - a terek és a merőleges síkokban - egyenes szakaszok (76. ábra).
A kocka vetülete három egyenlő négyzet.
A rajzban egy kocka és egy párhuzamos oszlop három dimenziót mutat: hosszúság, magasság és szélesség.
A 77. ábrán a részlet két téglalap alakú parallelepipedusból áll, amelyek mindegyike két négyzet alakú. Vegye figyelembe, hogy a rajzokon milyen méreteket ábrázolnak. A lapos felületeket vékony, metsző vonalak jelölik.
Hála a hagyományos jelnek # 9633; A részlet formája tiszta és egyenként.
11.2. A jobb háromszög alakú és hatszögletű prizmák kivetítése. Bázisok prizmák párhuzamos a vízszintes síkkal projekció ábrázolt ívelt az teljes méretű, és a frontális és a profil síkok - vonalszakaszok. Az oldalfelületek jelennek torzítás nélkül a projekciós síkon, amelyben azok párhuzamosak, és abban a formában vonalszakaszok azokra, hogy azok merőlegesek (ábra. 78). Face döntve a gépet projekció ábrázolt őket torz.
A prizmák méreteit a magasság és a bázis méret határozza meg. Az ábrán látható vonalkód-vonalak a szimmetria tengelyeit mutatják.
A prizmás izometrikus vetületek létrehozása a bázissal kezdődik. Ezután minden csúcsa a merőleges alap, amelyen sodrási hosszai azonos magasságú, és ezen keresztül a adatpontok végezzük egyenes, párhuzamos bordák egy bázis.
A téglalap alakú vetületek rajzolásával vízszintes vetítéssel is elkezdhetjük végrehajtani.
11.3. Szabályos négyszögletes piramis kivetítése. A piramis négyzet alakú alapját a H vízszintes síkra vetítik ki teljes méretben. Az átlós ábrák oldalirányú bordák az alap tetejétől a piramis tetejéig (79. ábra).
A piramis elülső és profilprojektjei egypólusú háromszögek.
A piramis méreteit a bázis két oldalának h hosszúsága és a h magasság határozza meg.
A piramis izometrikus vetülete az alapból indul. A központ az ábra kapott végezzük merőleges laikus erről a magassága a piramis és a kapott pont kapcsolódik, hogy a bázis csúcsok.
11.4. Henger és kúp kivetítése. Ha a körök fekvő bázisok a henger és egy kúp, párhuzamos a vízszintes síkkal H, azok előrejelzések ezen a síkon is körök (ábra. 80, b és d).
A henger elülső és profilprojektjei ebben az esetben négyszögek, a kúpok pedig egyenes háromszögek.
Vegyük észre, hogy minden vetületnél szimmetria tengelyeket kell alkalmazni, ahonnan a henger és kúp rajzok végrehajtása megkezdődik.
A henger első és profilprojektjei azonosak. Ugyanez mondható el a kúp vetületeiről. Ezért ebben az esetben a rajzon látható profilprojektek feleslegesek. Ezenkívül a 0 jelzésnek köszönhetően a henger alakját egy vetületben ábrázolhatjuk (81. Ebből következik, hogy ilyen esetekben nincs szükség három előrejelzésre. A henger és a kúp méretét h magasság és az alap d átmérője határozza meg.
A henger és a kúp izometriás vetületeinek előállítási módszerei megegyeznek. Ehhez az x és y tengelyek, amelyeken a gyémánt épült, készülnek. Oldala megegyezik a henger vagy kúp alaprészének átmérőjével. Az ovális be van írva a rombuszban (lásd a 66. ábrát).
11.5. A labda előrejelzései. A gömb összes vetülete olyan kör, amelynek átmérője megegyezik a gömb átmérőjével (82. ábra). Minden egyes kivetítésnél a középvonalak húzódnak.
A jelnek köszönhetően a gömb átmérője egy vetületben ábrázolható. De ha a rajz megnehezíti a gömb más felületektől való megkülönböztetését, akkor adja hozzá a "gömb" szót, például: "Sphere dmametra 45".
11.6. A geometriai testek csoportjának előrejelzései. A 83. ábra mutatja a geometriai testek egy csoportjának vetületeit. Mondhatod, hogy hány geometriai testet tartalmaz ez a csoport? Milyen testek ezek?
Miután megvizsgálta a képeket, meg lehet állapítani, hogy a kúp, a henger és a négyszögletes parallelepiped van rajta. Különböző helyzetben helyezkednek el a vetületek síkjaihoz és egymáshoz képest. Hogy pontosan?
A kúp tengelye merőleges a vetületek vízszintes síkjára, és a henger tengelye a vetületek profilsíkja. A parallelepipedus két oldala párhuzamos a vetületek vízszintes síkjával. A profilprojekcióban a henger képe a párhuzamos és a vízszintes - alul látható kép jobb oldalán található. Ez azt jelenti, hogy a henger a parallelepipedus előtt helyezkedik el, ezért a homlokoldalon lévő parallelepipedék egy részét szaggatott vonal jelzi. A vízszintes és a profilprojekteknél megállapítható, hogy a palack megérinti a parallelepipedét.
A kúp elülső vetülete a parallelepipedus vetületére vonatkozik. Azonban a vízszintes vetület alapján ítélve a parallelepiped nem érinti a kúpot. A kúp a henger bal oldalán és a párhuzamos tömszelencén helyezkedik el. A profilprojekcióban részben bezárja őket. Ezért a henger és a parallelepiped láthatatlan részeit szaggatott vonallal jelöltük.
20. Hogyan változik a profilkivágás a 83. ábrán, ha a kúp eltávolításra kerül a geometriai testek csoportjából?
1. A táblázatban fekvő maketteket, amint azt a 84. ábra mutatja, a. Számítsd ki a rajz szerint, hogy hány dákó van a közeledő első állásokban. Hány ellenfél van az asztalon? Ha a rajz szerint nehéz megszámolni őket, először próbálkozzon meg a darabok oszlopokkal történő bevételével és összehajtásával a rajz segítségével. Most próbálja megfelelően végrehajtani a feladatokat.
2. A négy oszlopban lévő táblázatban (84. ábra, b) találhatók dókák. Az ábrán két vetület látható. Hány trükk az asztalon, ha a fekete-fehér egyenlően oszlik el? A probléma megoldásához nem csak a vetítés szabályait kell ismernünk, hanem logikusan is érteni kell.
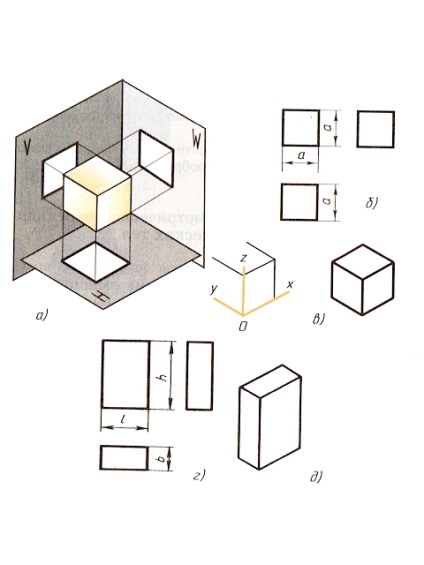
Ábra. 76. Cube és parallelepiped: a - vetület; b, d rajzok a négyszögletes vetületek rendszerében; c, d izometrikus vetületek
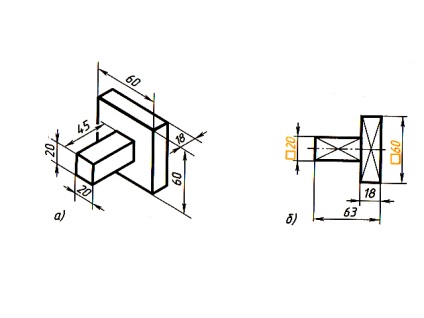
Ábra. 77. Részletes kép egy formában
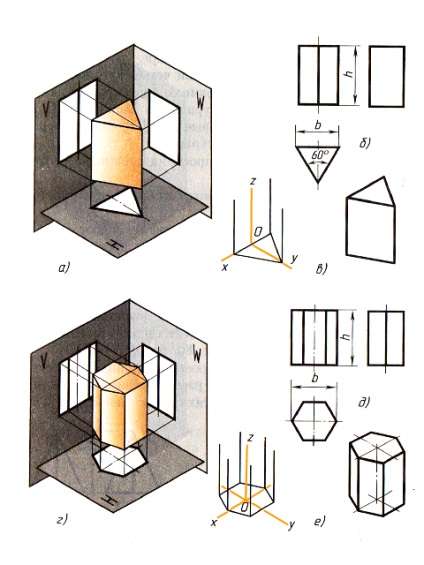
Ábra. 78. Prismák:
a, d - vetület; b, d - rajzok a négyszögletes vetületek rendszerében; c, e izometrikus vetületek
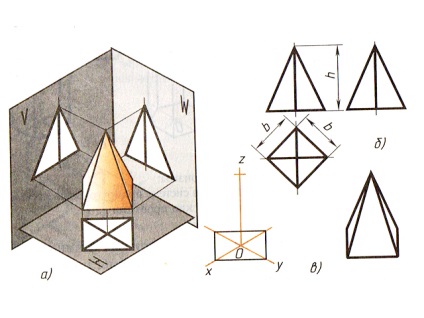
Ábra. 79. Piramis: a - vetítés; b - rajz a négyszögletes vetületek rendszerében; c egy izometrikus vetület
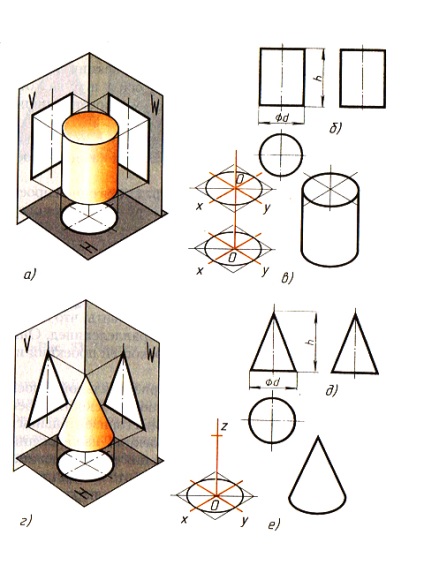
Ábra. 80. Henger és kúp: a, d - vetület; 6, d - rajzok a négyszögletes vetületek rendszerében; c, c - izometrikus vetületek
Ábra. 81. A palack képe egy formában
Ábra. 82. A labda előrejelzései
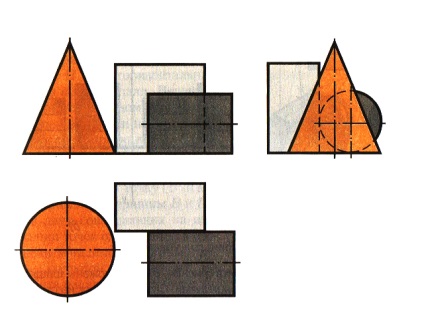
Ábra. 83. A geometriai testek csoportjának vetülete rajzolása
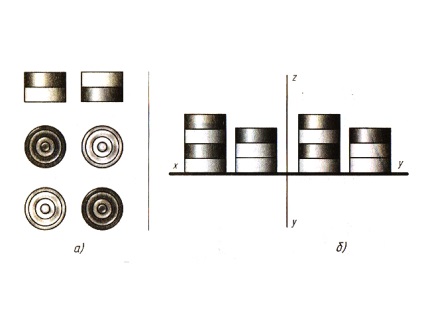
Ábra. 84. Gyakorlati feladatok



