A "funkció"
Funkció - az egyik alapvető tudományos koncepció; kifejezi a különböző tárgyak közötti kapcsolatot. A funkció koncepciója nem keletkezett azonnal, a koncepció kontúrjainak elsõ próbálkozása a 17. század végén történt. A koncepció bevezetésének őse Leibniz volt, valamint a Bernoulli testvérek is. A "funkció" kifejezés a Leibnizhez tartozik és a latin nyelvből származik. funkció "megvalósítása, végrehajtása".
A tizenkilencedik század elején egy függvénynek mint levelezésnek az elgondolása, amely szerint egy bizonyos X halmaztól kapott független változó egy másik "Y" változójú y változóvá alakult át, "kristályosodni kezdett.
Adjon meg néhány x értéket. t. e. ponthalmaz a valós tengelyen Ox, jelöljük D. Tegyük is tartalmaz két (X, Y) R. Ha bármely x értéknél a beállított X társul egy határozott törvény szigorúan meghatározott érték (bijektív egy másik y mennyiséget az Y készletből, akkor azt mondjuk:
· Az y mennyisége az x mennyiség függvénye, vagy hogy az x és y mennyiségek funkcionális függőséggel vannak összefüggésben
· Meghatározza azt a függvényt, amely az X halmazt az V. sorozatra térképezi
· Egy y = f (x) függvény szerepel az X halmazon.
Ez a funkciódefiníció grafikusan illusztrálható:
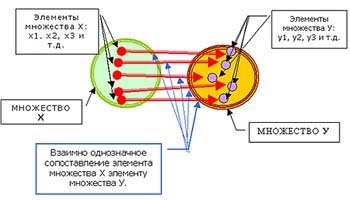
Az y függvény értékei az y függvény definíciójának X tartományából önkényesen tetszés szerint választhatók; ezért az x mennyiséget független változónak nevezik. A y függvény értéke. Ha az x független változó értéke már hozzárendelve van, nem választhat önkényesen. Ez az érték szigorúan meg lesz határozva, pontosan az, ami megfelel a független változó kiválasztott értékének. A függvény értékei a független változótól vett értékektől függenek, és változáskor változik. Ezért a függvény egy függő változónak is nevezhető.
Példaként tekintse meg a következő funkciókat.
1. példa A T hőmérséklet levegő ezen a helyen, mint óránként mértük a nap folyamán a függvénye integer-idő paraméterét t, kapó értékei t = 0, 1, 2, 3. 23. Valóban, minden egyes ilyen értékek megfelel a T értéke meglehetősen egy meghatározott értékű T, és ezért ennek a definíciónak megfelelően t függvénye. Itt a függvénydefiníció tartománya 24 "integrált" pontból áll. Ha a méréseket, hogy készítsen nem minden órában, és percenként, a hőmérséklet függvénye lesz az integrál érv fogadó már 24 x 60 = 1440 egymást követő egész szám.
2. példa Minden egyetemi hallgató egy adott kar meghatározott csoportjában tanul. Ha mi jelöljük X halmaza hallgatók ezen az egyetemen, és Y - számos képzési csoportok, azt mondhatjuk, hogy minden elemének X (minden tanuló) képezi le egy egyedülálló eleme Y (azaz a sáv, ahol tanul).