9 2 1 A síkok vágási módjának alkalmazása a problémák megoldásában
9.2.1. A síkok vágási módjának alkalmazása a
A 9. ábra. kúp és a félgömb.
A
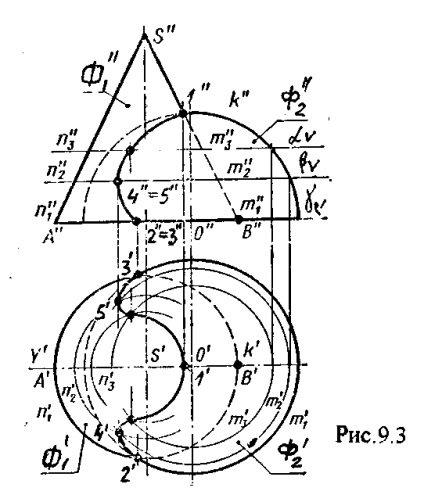
A keresztezési vonal megépítésének megkezdéséhez el kell kezdeni a keresztezési vonal megépítését, a referenciapontok megtalálása: a legmagasabb és a legalacsonyabb ebben az esetben. Más esetekben ez lehet a bal szélső vagy a jobb oldali pont. Mindkét felületet keresztezi a V síkkal és a forgástengelyen áthaladó felületekkel. Ennek eredményeként olyan keresztmetszeteket kapunk, amelyek ezen felületek elülső rajzai. Az 1 vázlatok metszéspontja a keresztezési vonalhoz tartozó pont.
Mivel mindkét felület alapjai ugyanabban a síkban helyezkednek el, a 2 és 3 körök metszéspontjai szintén közös pontok ezeknek a felületeknek.
Az 1,2,3 pontok a referenciapontok, az 1. pont a legmagasabb, a 2., a 3. pont a legalacsonyabb. Most mind a felületi síkja kereszt , alatt, a fenti 1. és 2. pont és a 3. metszi mindkét felülete körök N2 és M2 találni metszéspontja körök kapott m2 n2 = n2 4. m2 = 5.
A 4,5 pontok a kúp és a félteke metszésvonalához tartoznak. Ismételjük meg ezt a műveletet, a szükséges számú alkalommal, ezeknek a felületeknek egy metszésvonalát hozzuk létre.
9.3. A koncentrikus gömbök módszere
A
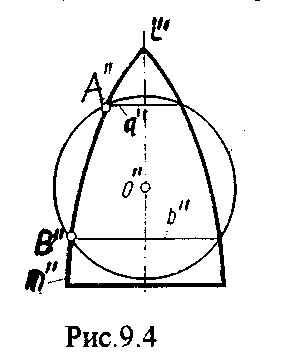
Ennek a módszernek az alkalmazása a következõ tulajdonságon alapul: Két tengelyirányú tengelyirányú tengely (együttes axiális felületek) keresztezik egymást a körök mentén. Valójában az m görbület forradalmi felületet képez az i forgástengellyel, az n görbét egy ugyanazon tengelyen lévő forradalmi felület képez. Ha m = A, akkor az "A" pont egy olyan kört ír le, amely mindkét felületen közös, így a metszéspontjuk vonala. (9.4 ábra).
Ha i tengelye merőleges a síkra H, akkor az által leírt kört az A pont vetített a frontális síkban a nyúlvány a szegmens és egy vízszintes síkban egy kör.
Az eddigiekből az alábbi következtetések vonhatók le:
1. Annak érdekében, hogy segítse a szelő szféra által metszett két kört adott forgási felület a gömb középpontján kell lennie metszéspontjában tengelyeinek ezeket a felületeket.
2. Ha az előre meghatározott forgástengely síkjával párhuzamos vetítési felületek, metszi a kör a kisegítő vágás egy gömb ezen felületek az előrejelzések ezen a síkon szegmensek.
Most megfogalmazhatjuk a koncentrikus szekeres szféra módszere alkalmazásához szükséges feltételeket:
1. A felületi adatoknak forradalmi felületeknek kell lenniük;
2. Ezen felületek forgási tengelyének metszi egymást;
3. Az ilyen felületek forgástengelyén áthaladó síknak párhuzamosnak kell lennie egy bizonyos vetületi síkkal.
A keresztezési vonal építése ellenőrzési pontok felépítésével kezdődik (9.5. Ábra). A támogatási pontok megépítéséhez minimális sugárral kell rendelkeznünk. A minimális sugár gömbje fel van tüntetve egy felületen és metszi a második.
A referenciapontok a kúppal és a hengerrel való keresztezés körének C és D közös pontjai. A referenciapontok magukban foglalják ezen felületek elülső rajzainak metszéspontjait is. Az OtiotFced szegmens, ahol az ezen felül elhelyezkedő rajzok metszéspontja az O определяет ponttól a legnagyobb sugár szféráját határozza meg.
Közbenső pontok létrehozásához szükséges egy R sugarú gömb választása, ahol Rmin egy ellipszis