Elektrosztatikus potenciál

Uraim, köszönjük mindenkinek!
Most emlékeznünk kell egy kapcsolatra. Térjünk vissza néhány cikkhez a feszültségről szóló cikkhez. Görgessen lefelé. Egy kicsit alacsonyabb. Igen, itt. Az a pontig, ahol nem ideális feszültségforrásnak tekintettük. Bár mi van ott, tudom, hogy legtöbbjük nem hivatkozott. Köztudott, hogy néha túl lusta, hogy egy kattintással egérrel végezzen és mindent látni akar itt és most. A VC fejlesztõi chipet forgatnak, így a közelmúltban a hyphos lejátszása automatikusan vált. Ezt a tendenciát követve ezt a képet is kihúzom ebből a cikkből. Ezt az 1. ábrán mutatjuk be.
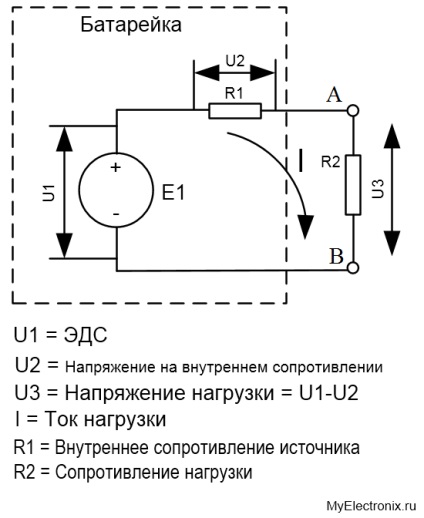
1. ábra - Nem ideális forrás
Emlékeztek erre? Itt van egy tápegység, amelynek EMF egyenlő E1-gyel és egy belső ellenállása R1-vel egyenlő. Ez a forrás bizonyos R2 terhelésnél működött. és megadja az U3 feszültséget és az áramot.
De aztán még mindig nem beszéltünk az Ohm törvényéről, és nem vettük figyelembe, hogy pontosan mi az U3. Most, az Ohm-törvényről szóló cikkből tudjuk, hogy ha egy áramot egy R1 ellenállással rendelkező ellenálláson keresztül áramolok, akkor ez a feszültség az ellenálláson
Ennek megfelelően most könnyű megtalálni az U3 feszültséget:
Igen, uraim, egy ilyen tökéletlen forrásban a forrás kimenetén a feszültség függ a jelenlegi áramlástól, és nem a legjobb oldalon. Magas áramerősség esetén a feszültség a tápegység kimenetén sag. hogy az áramforrás nem tartja a terhelést. Azok a források, amelyek nem tartják a terhet, ez természetesen olyan mókás téma, amely sok fejfájást képes átadni a fejlesztőknek, de most már egyáltalán nem róla. Emlékszem, egyszer csináltunk nagyfeszültségű tápegység magnetron adó KGHM ... ... nos, ez jobb, valahogy egy másik alkalommal ... A mi feladatunk abban a pillanatban az volt, hogy itt, az arány a feszültség a nem ideális teljesítmény
Vagyis, ha van egy forrás az áramkörben, egy EMF egyenlő E-val és egy ellenállás R-val egyenlő. És az összes áramban áramló áramkörben, a feszültséget az áramkör végein tudom kiszámítani. Hasznos arány, uraim, azt javaslom, hogy vegye el a képletedre!
Javítsuk meg a példát. Tegyük fel, hogy van egy 1,5 V-os EMF-es és 0,5 Ohm-os belső ellenállása. 1 ohm ellenállással kapcsoljuk. Tény, hogy egy normál akkumulátorhoz ez elég kemény mód, és nem tart sokáig, így a gyakorlatban nem ajánlom megismételni, és legalább 10-nél többször ellenállni. Azonban ez a példa jobban mutatja az akkumulátor belső ellenállásának hatását a nagy feszültségű kimeneti feszültségre (jól, vagyis kis terhelés esetén).
Az akkumulátor teljes ellenállása nyilvánvalóan a belső ellenállás és a terhelésállóság összegéből áll:
Az Ohm törvénye szerint az áram a körben
És most, az új képlet szerint, a feszültséget az akkumulátor kimeneténél tartjuk
Rengeteg időt töltöttünk olyan kérdésekben, amelyek első látásra úgy tűnnek, mint offtopic. Azonban a jövőben egyértelmű lesz, miért tartjuk ezt az arányt itt. Most menj a lényegre, hogy mi van a cikk címében.
Valószínűleg azt hallottad, hogy néha a feszültséget potenciális különbségnek nevezik. Azonban még nem mutattuk be a potenciál fogalmát, és minden bizonnyal nem volt különbség. Uraim, egyszerre fogom mondani, nem fogjuk fontolóra venni a potenciális formális definíciókat, amilyen például a fizika során. Nem mintha nagyon nehéz lenne ott, csak a jövőben ez a formális meghatározás nem fog minket sokat segíteni. Könnyű a google, és megtalálni, ha hirtelen érdekessé válik, nem okoz problémákat. Most fontos számunkra, hogy el tudjuk képzelni, hogy a potenciál kapcsolatban áll-e a feszültséggel és hogyan határozható meg az áramkörben. Nézzük a rajzot
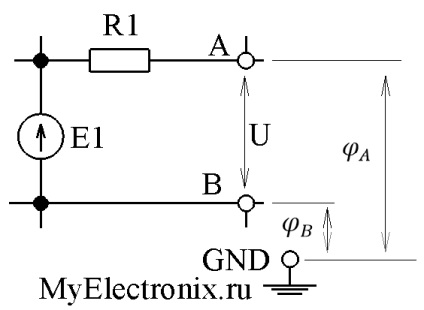
2. ábra - A potenciál meghatározása
Az áramkör egy töredékét mutatja. Amit magában foglal magában - ebben az esetben egyáltalán nem. Egy EMF E1-es forrást és R1 ellenállást rajzoltam. Lehet, hogy van valami más, ami tetszik. A GND az áramkör közös pontja. amelyhez minden fő feszültség létrejön, a jelszintek számítanak és minden ilyen. Ilyen pont minden rendszerben. Nagyon gyakran megalapozott, vagyis valamilyen módon közvetlen kapcsolatban áll a Földdel (igen, az a legfontosabb, amellyel mindannyian járunk), bár ez nem kötelező követelmény. Figyeljünk az A és a B sorkapcsokra. Feltételezzük, hogy van köztük valamilyen feszültség U. A kiszámítása most már teljesen irreleváns. Csak feltételezzük, hogy van egy U feszültség. Ugyanakkor az A pont és a GND áramkör közös pontja között bizonyos feszültség φA működik. és a B pont és az áramkör közös pontja között egy bizonyos feszültség φB. Tehát ebben az esetben azt mondják, hogy az A pont potenciálja φA. és a B pont potenciálja egyenlő a φB-vel. Ebben az esetben a GND pont potenciálja nulla. Ismét megjegyzem - ez nem egy formális definíció a fizikában, de közelebb van a gyakorlathoz. Hogyan kapcsolhatjuk össze az A és B pontok potenciálját az U feszültséggel, amely ezen pontok között működik? Ezek nagyon egyszerűen kapcsolódnak egymáshoz:
Úgy gondolom, hogy ez a kapcsolat nyilvánvaló, figyelembe véve, hogy az A és B pontok potenciáljait a GND egy közös pontjából mérjük.
Még egy érdekes esetet említek. Különösen érdekli, hogy gyakran foglalkozik a gyakorlatban. Például, maga a B pont közvetlenül kapcsolódik a GND rendszer közös pontjaihoz. Azt feltételezzük, hogy a B φ B pont potenciálja nulla, és az A φ A pont potenciálja egyenlő az U feszültséggel.
Amint azt látjuk, önmagában a potenciál általában viszonylagos. A feszültség, amely potenciális különbség, nincs ilyen. Amikor kivonjuk az egyik potenciált egy másikról, ez a relativitás megszűnik.
Talán kiderült egy kicsit ostoba. Tehát mindig amikor valami rokonról beszél, amely nincs egyértelmű referenciapontjával. De ha ismét röviden mondom, uraim, e szövegmennyiségből azt akartam, hogy egy egyszerű relációt viseljen, hogy ha az A és B pontok közötti feszültség egyenlő az U.-val, akkor
ahol φA és φB az A és B pontok potenciálja.
Most, kombinálva ezzel a két képlet együtt
Ez történik? Az áramkör végei közötti potenciálkülönbség megegyezik az ebben az áramkörben működő forrás EMF-rel, amely mínusz az áramkörben lévő áram terméke az áramkör terhelési ellenállása által. Uraim, azt javaslom, hogy emlékezzetek erre az utolsó kifejezésre. És még jobb tudni mind a három utolsó írott képletet. A jövőben szükségünk lesz rá. És Kirchhoff második törvényének származtatása során mindig ezt folyamatosan használjuk.
Ez minden, uraim. Köszönöm a figyelmet és hamarosan látlak!