Bemutatás a harmonikus oszcillációs grafikon témájára
1 A harmonikus oszcilláció grafikonja

2 A rendszeresen ismétlődő mozgásokat oszcillációnak nevezik

3 Mechanikus vibrációkat használnak a leggyorsabb betonozáshoz speciális vibrátorokkal; a fogak szinte fájdalmas fúrásához. Akusztikus rezgések szükségesek a hang fogadásához és reprodukálásához, és elektromágneses rezgések szükségesek a rádió, a televízió és az űrraketták közötti kommunikációhoz. Az elektromágneses vibrációk új híreket jelentenek a csillagok során előforduló összetett folyamatokról, a távoli galaxisok robbanásairól, olyan furcsa dolgokról, mint a pulzárok (neutroncsillagok), fekete lyukak stb. Az elektromágneses rezgések segítségével a tudósok a Hold hátsó oldaláról képet kaptak, és örökre a Vénusz felhői zárták.

4 fluktuációk kíséri és biológiai folyamatok, például, hallás, látás, észlelés ultraibolya (használják számos biológiai fajok) a gerjesztési idegszövet, szív és az agy. A szív vagy az agy munkájának rögzítésénél az orvosok elektrokardiográfiákat és enkefalogramokat kapnak. A szavak az alkotó a tanítás a bioszféra Vernadszkij: „Körülöttünk bennünk, mindenhol, bárhol, megszakítás nélkül, az örök változás, amely egybeesik, és összeütközött, a sugárzás különböző hosszúságú - a hullámok, amelyek hossza mérjük tíz milliomod frakciói milliméter hosszú, mért kilométer ".

5 Az ingadozások azonban nem mindig hasznosak. A gép rezgése a vágókészülékre és a munkadarabra hat, és házassághoz vezethet; a folyadék rezgése a rakéta tüzelőanyag-tartályaiban fenyegeti integritását, és a repülőgép szárnyainak rezgése kedvezőtlen körülmények között katasztrófához vezethet. Még egy jól szorított anya a rezgés hatására gyengül és a gépet felrobbantják. És a legszörnyűbb, hogy a vibráció hatására a fémek belső szerkezete megváltozik, ami az úgynevezett fáradtsághoz és a későbbi váratlan romboláshoz vezet.

6 rezgések magyarázható az esetben a híd esés, amellyel megszerezték a katonai egység, valamint a megsemmisítés hidak alatt hurrikánok, katasztrófák kovácsolás üzletek, ahol több mechanikai kalapácsok kezdett dolgozni tapintat. Az oszcilláció harmonikus rezgései, amelyekben a fizikai (vagy bármely más) érték idővel változik szinuszos vagy koszinus joggal.

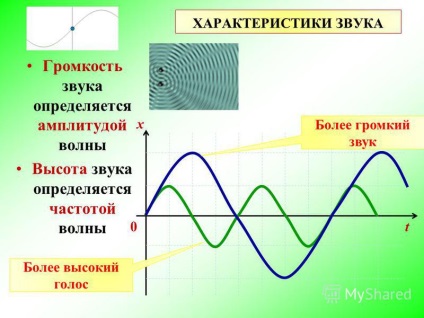
7 HANG JELLEMZŐK A hangerőt a hullám amplitúdója határozza meg A hang hangmagasságát a hullám frekvenciája határozza meg t x Hangosabb hangzás Magasabb hang 0
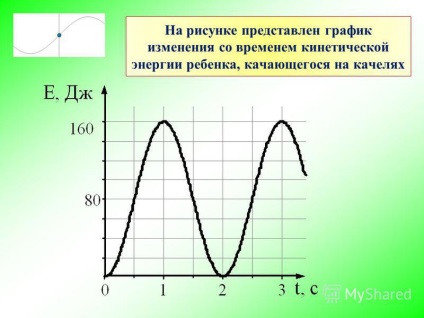
8 Az ábra a lendületben lengő gyermek mozgási energiájának időbeli alakulását mutatja
9 Az ábra egy karakterlánc egyik pontjának oszcillációját ábrázolja
10 Az ábra azt mutatja, hogy a gömb középpontjának koordinátája függ a rugótól időben felfüggesztve.
11 Megjegyezzük, hogy az emberek által vezérelt ingadozások nagyon hasznosak. Ugyanakkor veszélyes ellenséggé válhatnak. Ezért képesnek kell lenni arra, hogy tanulmányozza a rezgéseket, ismerje meg tulajdonságait. És itt nem tehetünk matematikai számítások nélkül. Harmonikus oszcillációk a pontnak az a = Asin (t +), ahol A a oszcillációk amplitúdója, frekvenciája, az oszcilláció α-kezdeti fázisa, t az idő koordinátája.
12 A y = A sin (x +) vagy y = A cos (x +) függvényének leképezéséhez szükséges: 1) az adott függvény y = A sin (x + I) vagy y = A cos (x + /); 2) készítsünk egy y = sin x vagy y = cos x görbét; 3) húzza (összenyomja) az y tengelyre együtthatóval; 4) az abszcisszák tengelyével az A együtthatóval megnyújtva (préselés); 5) az abszcissza tengely mentén párhuzamosan haladjon egy mennyiséggel.
13 YXY = cos x Ábrázoljuk a függvény az y = 2 cos (2 x + 2π3) 1), így egy előzetesen meghatározott függvény az űrlap y = 2 cos2 (x + π3) (vegye ki a kifejezést (2 x + 2π3) közös tényező 2 per konzol) 2) ábrázoljuk az y = cos x görbét; 3) A diagramot y = cos x; (tükrözi az y = cos x szimmetrikus az ox tengelyre) y = cos x 4) a koordináta tengelyhez 2-es koefficienssel tömörítjük, megkapjuk az y = cos 2x gráfot; y = cos 2x y = 2 cos2 (x + π3) 5) Az abszcissza tengelyből 2-es együtthatóval húzza ki, akkor kapjuk meg az y = 2cos 2x görbét; 0 6) az abszcisza tengely mentén átadjuk ezt a gráfot balra π3 értékkel; megkapjuk a függvény grafikonját y = 2 cos (2 x + 2π3) y = 2 cos (2 x + 2π3) y = 2cos 2x hasznos kivitelezni kiszámításával, például a függvény értéke a következő képlet szerint y = 2cos (2x + 2π3) x = 0 : y = 2cos (π3) = 2 cos 2π3 = 2 (0,5) = 1 A grafikonnak tartalmaznia kell egy koordinátájú pontot: x = 0, y = 1 π3π3