Clarke-Wright módszer
BEVEZETÉS.
A leírt módszert a "Egyszerű útvonalformáció: Kártyával történő munka: Az optimális szállítási lehetőségek kiszámítása"
A cikk „Optimization tervezés a szállítás. Klaszterek algoritmus k-means (K-means)” volt, azt mutatják, hogyan lehet megszerezni az optimális útvonalat a megadott számú A / teherautók a megadott helyre történő szállítás, a szállítási kapacitás nem veszik figyelembe.
Ebben a cikkben megmutatjuk, hogyan lehet megtudni a számát szükséges A / szállítási figyelembevételével a teherbíró képességét generálni az optimális útvonalat.
Tehát a feladat az, hogy megtalálja a leginkább nyereséges útvonalat a forgalom, átmenve egyszer ezen pontok, majd visszatér a kiindulási pont (alap). A probléma ezen megfogalmazásában az optimális kritériumok a következők: a jármű maximális megtett távolsága a test maximális terhelésével.
A megfogalmazott probléma az úgynevezett "utazó ügynök problémája". Számos matematikai módszer létezik, amelyek lehetővé teszik számunkra, hogy pontos és közelítő megoldást találjunk a feltett problémára. A pontos megoldást nyújtó módszerek közül a legismertebb:
Ezeknek a módszereknek a legfőbb hátránya a magas időbeli és kapacitív komplexitás, amelyet nagy számban kell figyelembe venni. Az "utazási ügynök probléma" megoldásának hatékony (az átfogó keresési módok csökkentése) módszerek heurisztikus módszerek. Ezek közül a legnagyobb alkalmazást találtam:
- "A genetikai algoritmusok módszere"
- "Clark-Wright módszer"
- "A hangyabogó algoritmusa"
- "A legközelebbi szomszéd módszer"
- "A legközelebbi város bevonásának módja"
- "A legolcsóbb befogadás módszere"
A probléma megoldásához a Clark-Wright módszer a legalkalmasabb módszer. Ez a hozzávetőleges, iteratív módszerek számára utal, és számítógépes megoldásként használható a közlekedés problémájára. Az oldat hibája nem haladja meg az átlagos 5-10% -ot. A módszer előnyei az egyszerűség, a megbízhatóság és a rugalmasság, amelyek lehetővé teszik a probléma végső megoldását érintő számos további tényező mérlegelését.
Vegyük például figyelembe a Clark-Wright módszer alkalmazását.
A probléma leírása.
A rakomány terminál (raktár) kiindulópontjától 12 árucikkre kell szállítani.
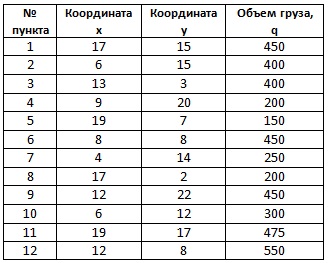
1. táblázat: A címzettek keresletének koordinálása és mennyisége
A rakomány terminál (raktár) koordinátái: x0 = 10, y0 = 15. A szállításhoz a szállítást legfeljebb 1500 egység kapacitással lehet használni.
KÉRDÉS: Mennyit kell szállítani az áruk szállításához? Melyik szállítási rendszer optimális?
ELŐKÉSZÜLETI MUNKA.
Jegyezd meg ezeket a pontokat a Descartes-koordinátarendszerben. A nagykereskedelmi bázis és a 12 címzett helyét, valamint az egyes címzettek szállítási mennyiségét az 1. ábrán mutatjuk be.
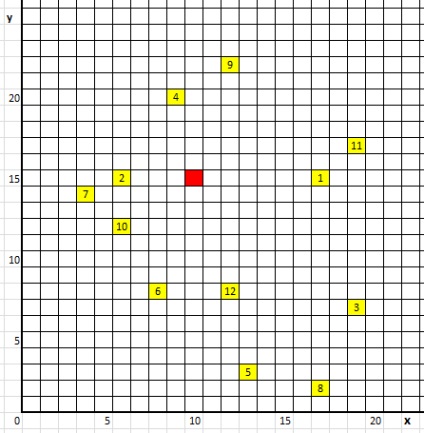
1. ábra: Az alap és a szállítási pontok elhelyezkedése
Az útvonalak kezdeti terve azt feltételezi, hogy a rakomány minden egyes címzett részére külön útvonalat szervez (lásd a 2. ábrát). Például a vezető 450 darabnyi tételt tölt be a szervezetbe. és átveszi az 1-es pontra, kirakja, majd visszatér a bázishoz, és megszerzi a második 400 darabos tételt. és továbbítja a 2. pontba, stb. Így a szállítás kezdeti sémája csak az autó sugárirányú útvonalát foglalja magában, és a radiális útvonalak száma megegyezik a címzettek számával. Ebben az esetben a szállítási rendszer 12 radiális útvonalból áll.
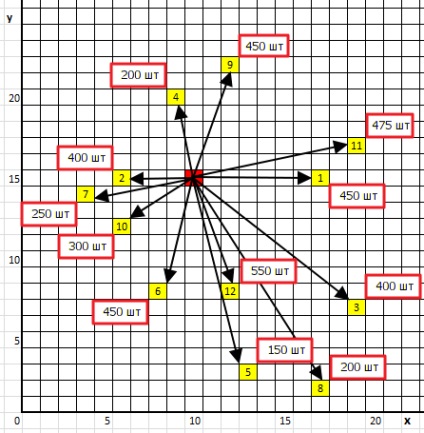
2. ábra A rakomány szállításának kezdeti terve
A módszer lényege, hogy a kezdeti szállítási sémától kezdve az optimális szállítási sémára kell költözni. E célból egy kilométeres győzelem fogalmát vezetik be.
A 3. ábra két szállítási sémát mutat be. Az "A" rendszer (balra) biztosítja az áruk szállítását az 1. és a 2. pontban sugárirányú útvonalak mentén. Ebben az esetben a járművek teljes futásteljesítménye:
La = d01 + d10 + d02 + d20 = 2d01 + 2d02
A B szállítási rendszer feltételezi, hogy az 1. és a 2. pontot a gyűrűút mentén szállítják. Ezután a járművek megtett távolsága:
A B rendszer a járművek kilométerteljesítménye tekintetében általában jobb eredményt biztosít, mint az A rendszer. Ezért az "A" rendszerből a "B" rendszerbe való lépéskor a következő kilométeres győzelmet kapjuk:
S12 = La-LB = d01 + d02-d12
Általában van egy kilométeres kifizetés:
ahol Sij az i és j, km pontok összekapcsolásával nyert kilométer-kifizetés; d0i, d0j - a nagykereskedelmi bázis és az i. és j., km közötti távolság; dij az i és j, km közötti távolság.
A kapott értékeket a 2. táblázatban adjuk meg. Hol vannak a di (a mátrix jobb felső sora) és a kilometer közötti távolságok a Sij (a mátrix bal alsó része) között.
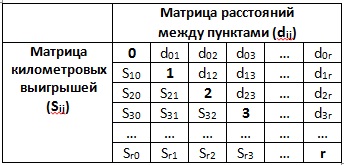
2. Táblázat Távolság mátrix és kilométer győzelem
Most vissza a példánkhoz. A táblázatból. 1 az adatokat vesszük:
- 0. pont (ez az alap): x0 = 10, y0 = 15
- 1. tétel: x1 = 17, y1 = 15
- 2. bekezdés: x2 = 6, y2 = 15
- 3. pont: x3 = 13, y3 = 3
- és így tovább.
A 0 és 1 pont közötti d01 távolságot a képlet szerint számítjuk ki:
Hasonlóképpen megkapjuk a távolságot:
- a 0 és a 2 pontokhoz. d02 = 4
- a 0 és a 3 pontokhoz. d03 = 12,37
- az 1. és 2. tételeknél. d12 = 11
- az 1. és a 3. tételnél. d13 = 12,65
- a 2. és a 3. tételnél. d23 = 13.89
- stb.
Ezután az i és j pontoknál kapjuk meg a Kilométer kifizetést Sij = d0i + d0j - dij.
- az 1. és a 2. pontra. S12 = d01 + d02 - d12 = 7 + 4 - 11 = 0
- az 1. és a 3. pontra. S13 = d01 + d03 - d13 = 7 + 12.37 - 12.65 = 6.72
- a 2. és a 3. pontra. S13 = d02 + d03 - d23 = 4 + 12.37 - 13.89 = 2.48
- és így tovább.
A kapott értékek a 3. táblázatban vannak feltüntetve, ahol a pontok dij (a mátrix jobb felső része) és a kilométeres gyűrű (a mátrix bal alsó része) közötti távolságok a következők:
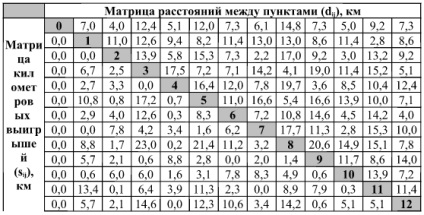
3. táblázat: Becsült távolságmátrix és kilométernyerés
Most, hogy minden szükséges előkészítő munkát elvégeztünk, közvetlenül a probléma megoldására fogunk lépni.
A CLARK-WRIGHT ALGORITHM LEÍRÁSA.
A kilométeres nyerés mátrixban megtaláljuk a cellát (i *, j *) a maximális kilométer-nyeréssel Smax:
A következő három feltételnek teljesülnie kell:
- az i * és j * pontok nem szerepelnek ugyanabban az útvonalon;
- az i * és j * pontok azoknak az útvonalaknak a kezdő és / vagy végpontjai, amelyekhez azokat tartalmazzák;
- a sejt (i *, j *) nincs lezárva (azaz az algoritmus előző lépéseiben).
Ha lehetséges olyan cella megtalálása, amely megfelel a három meghatározott feltételnek, akkor folytassa a 2. lépéssel. Ha ez nem lehetséges, akkor folytassa a 6. lépéssel.
Az i * pontot magában foglaló útvonalat az 1. útvonalnak jelöltük. Ennek megfelelően az útvonalat, amely magában foglalja a j * pontot, a 2. útvonalnak nevezzük.
Bemutatjuk a következő jelölést:
N = - a címzettek halmaza;
- az 1. útvonalon szereplő elemek részhalmaza;
- a 2. útvonalat alkotó elemek részhalmaza.
Nyilvánvalóan (az 1. lépés 1. feltétele szerint).
Az 1-es és 2-es útvonal mentén kiszámítjuk az összes szállítási mennyiséget:
ahol qk a k-edik item kereseti mennyisége, db (lásd a 4. táblázatot).
Ellenőrizzük a következő feltételt:
ahol c az autó rakománya, db.
Ha a feltétel teljesül, folytassa a 4. lépéssel. Ha nem, folytassa az 5. lépéssel.
Összevonása útvonalak 1. és 2. egyetlen körút X. Azt feltételezzük, hogy a lényeg i * a végső cél az útvonal 1 és bekezdés j * - a kiindulási pont az útvonal 2. Amikor láncolás útvonalakat az 1. és 2. megfelelnek a következő feltételeknek:
- az 1-es útvonal pontjai helyének sorrendje az elejétől az i * pontig nem változik;
- az i * pont j * -kal van társítva;
- a 2. ponttól a j * -tól a végéig terjedő pontok helyzete nem változik.
Ismételje meg az 1-4. Lépéseket, amíg a következő ismétlés során nem találja az Smax értéket, amely megfelel az 1. lépésben foglalt három feltételnek.
Számoljuk ki a járművek teljes futásteljesítményét.
A SEKVENCIÓS MEGOLDÁS LEÍRÁSA A CLARK_RIGHT MÓDSZERBEN.
A probléma egymást követő megoldásának teljes folyamata a 4. táblázatban található.
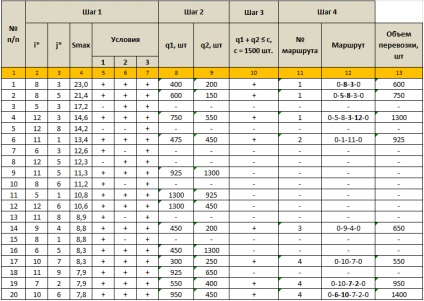
4. táblázat A probléma megoldásának folyamata és közbenső eredményei
Az 1. rovat az iterációs szám.
4. keretes szöveg - az Smax legnagyobb kilométernyeremény értéke.
Az 5., 6. és 7. oszlopok az 1., 2. és 3. ellenőrzési feltételek eredményei az 1. lépésben. "+" Pozitív eredmény, "-" negatív eredmény.
8. és 9. oszlop - az 1. útvonal mentén található forgalom nagysága, amely magában foglalja az i * (q1) pontot és a 2. útvonalat, amely magában foglalja a j * (q2) tételt.
10. rovat - annak a feltételnek a vizsgálata, ahol c a jármű rakomány kapacitása. "+" - állapotfelmérés pozitív eredménye, "-" - negatív eredmény.
11. oszlop - a gyűrűút sorszáma (a döntés során csak négy kerek útvonal érkezett, lásd a 4. ábrát).
12. oszlop - ez az iteráció során kialakult kör alakú út felépítése.
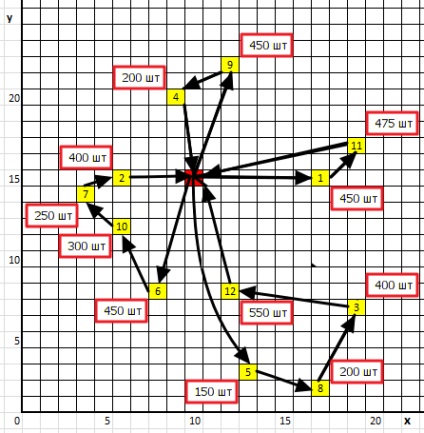
4. ábra: Az optimális szállítási rendszer grafikus ábrázolása
Gondoljuk meg, hogyan történik egy lépésről lépésre történő keresés a probléma optimális megoldására. Kezdjük azzal a ténnyel, hogy a kiindulási terv tizenkét sugárirányú útvonalból áll, amikor a rakomány szállítása minden rendeltetésre külön útvonalon történik (lásd a 2. ábrát). Ugyanakkor a járművek teljes futásteljesítménye (lásd a háromszögletű mátrixot, 3. táblázat):
L0 = 2 * d01 + 2 * d02 +. + 2 * d012 = 2 * 7,0 + 2 * 4,0 + 2 * 12,4 + 2 * 5,1 +. + 2 * 7,3 = 195 km.
Most lépésről lépésre megkezdődünk a probléma új, optimális megoldására való áttérés, amely a sugárirányú útvonalak gyűrűs összekapcsolásával csökkenti a járművek teljes futásteljesítményét (grafikusan ez az új megoldás a 4. ábrán látható).
- Két radiális útvonalat egyesítünk: 0-8-0 (szállítási mennyiség 200 db) és 0-3-0 (szállítási mennyiség 400 db) Az általános körgyűrűhöz (az 1. szám alatt) 0-8-3-0 (szállítási mennyiség: 600 db.). Ugyanakkor a gépjárművek teljes futásteljesítménye 23,0 km-rel csökken.
- A körgyűrűhöz 1 - 0-8-3-0 (600 db) Csatlakoztassa a 0-5-0 sugárirányú útvonalat (150 db). Ugyanakkor az 5. pont a 8. ponthoz kerül. Ennek eredményeképpen kapunk egy új szerkezetet a 0-5-8-3-0 (750 db) gyűrűs útvonalon. A járművek teljes futásteljesítményét további 21,4 km-rel csökkentik.
- Figyelemre méltó az, tapadó pontot szekvencia egy körkörös útvonalon: nevezetesen 0-5-8 -3-0 nem 0-5-3-8-0 vagy 0-8-3-5-0.
- Ha i * = 8 és j * = 5, akkor az egyesítés után meg kell állni az útvonalon egymás után.
- A 3. és 5. pont kombinációja 17,2 km nyereséget jelentene. De ez a társítás lehetetlen, mivel mindkét tétel már része a gyűrűvonalnak 1 - 0-5-8-3-0, és csak különböző útvonalakból lehet kombinálni a pontokat. Így kijelentjük az 1. feltétel megsértését, és folytatjuk a következő iterációt.
- A kerületi útvonal № 1 - 0-5-8-3-0 (. 750 db) szomszédosak a radiális irányban 0-12-0 (150 db.). Ebben az esetben, a fenti 12. csatolja a 3. lépéshez, így kapjuk az új szerkezet a gyűrű útvonal 0-5-8-3-12 -0 (1300 db.). A járművek teljes futásteljesítménye 14,6 km-rel csökken.
- A 12. és a 8. elemek nincsenek kombinálva, mivel már az 1. körgyűrű részét képezik (az 1. feltétel megsérti).
- Két radiális útvonalat egyesítünk: 0-1-0 (450 db) és 0-11-0 (475 db) az általános körgyűrűhöz (2-es szám alatt) 0-11-1-0 (925 db). Ugyanakkor a gépjárművek teljes futásteljesítménye 13,4 km-rel csökken.
- A 3. és 6. pont nem kombinálható a 2. feltétel megsértése miatt. A 3. bekezdés az 1. körgyűrű részét képezi, és ebben az úton egy "közbenső" pozíciót foglal el, vagyis a 8. és 12. pontokhoz kapcsolódik: 0-5-8-3- 12-0. A 0-6-0 sugárirányú útvonalat az "1" gyűrűvonalhoz csatlakoztathatjuk a "szélsőséges" pontok - 5 vagy 12 oldaláról, de nem lehet a "közbülső" 3 és 8 pontokhoz csatolni.
- Ismételje meg az indokolás logikáját, mint az előző 7 iterációban. Csak azt vesszük észre, hogy a 9., 11., 12., 16. és 18. iterációkban az unió nem csak az állapot megsértése miatt történt
Iterációk 21-től 60-ig
- Már nincs értelme, hiszen ezek végrehajtása nem jár a szállítási terv módosításával.
A 20 iteráció teljes kilométernyerése:
S = 23,0 + 21,4 + 14,6 + 13,4 + 8,8 + 8,3 + 7,9 + 7,8 = 105,3 km
és a járművek teljes futásteljesítménye, illetve:
L1 = L0-S = 195 -105,3 = 89,7 km
A grafikailag optimális szállítási sémát az 1. ábrán mutatjuk be. 4. Mint látható, az optimális szállítási rendszer négy kör alakú útvonalat tartalmaz (az eredeti 12 radiális útvonal helyett). A járművek teljes futásteljesítményét a következő képlet határozhatja meg:
, ahol Li az i-es út hossza, km; r az útvonalak száma.
Vegyük például a 0-5-8-3-12-0 gyűrűs útvonalat. Az útvonal hosszát a képlet határozza meg (lásd a 4. táblázatot):
L1 = d0,12 + d12,3 + d3,8 + d8,5 + d5,0 = 7,3 + 5,1 + 4,1 + 5,4 + 12,0 = 33,9 km.
Hasonlóképpen kiszámítjuk a fennmaradó útvonalak hosszát.
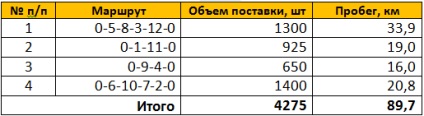
A MEGOLDÁS EREDMÉNYEI.
A probléma megoldásának eredményeit a következő táblázat foglalja össze: