A háromszögek egyenlőségének jelei (15
§1. A háromszög egyenlőségének első jele.
1. Húzza az ABC háromszöget. Adja meg a háromszög meghatározását.
2. a) Írja le a háromszög összes lehetséges szimbólumát.
b) Adja meg: a C szöggel szemben fekvő oldal; az SM oldalán fekvő szög; EU-szomszédos szögek; szög az EU és az EM oldalai között (1.1. ábra).
c) Mérje meg a háromszög kisebb oldalát és nagyobb szöget, és jegyezze fel a mérési eredményt (ábra.1.1).
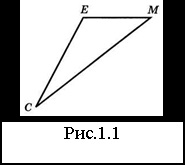

a) # 8710, CEM _____________________;
b) Az oldal ____ a C szöggel szemben helyezkedik el; az SM oldalán __________; Az EU oldalán a sarkok _______; az EU és az EM Felek között - sarok ______;
c) EM = _____ cm; # 8710; CEM = _______.
3. Keressen egyenlő háromszögeket, jelezze egyenlő elemeiket (1.2.
b) Átlátszó film használata.
Tedd fel ABC # 8710; körbe, majd alkalmazza a filmet a # 8710; A1B1C1. Az illeszkedés megkönnyítése érdekében nyomja meg a gombot az A1 gombbal (1.6 ábra).
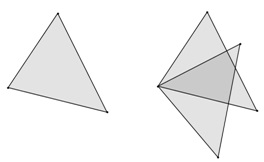
3. Határozza meg, hogy hány pár egyenlő elem elegendő a háromszög egyenlőségéhez. Nevezze meg ezeket az elemeket. Állítsd be a tételt.
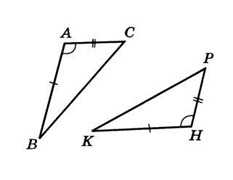
Ha az ABC háromszög a háromszögre helyezkedik el, az AB oldal MCN-je az MC oldala felé mutat. A hangszóró oldalán található az MN oldalán.
A fegyveres erők oldala egybeesett az SC oldalával? Magyarázza el a választ.
A megoldás. Mivel a felek AB és az AU a felekhez igazodtak _____. akkor a B és C pontok egybeesnek a pontokkal ______. Következésképpen a BC és ____ szegmensek végei igazodnak, így a BC és a CN szegmensek ______.
1. Olvassuk el a tankönyv első jelének tételéről szóló nyilatkozatot, a tankönyvben.
2. Írja le a tétel állapotát.
3. Hajtson rajzot.
4. A tankönyv szövegében olvassa el és elemezze a tétel bizonyítékát.
5. Írja le a bizonyíték fogalmát a notebookba:
Válaszolj a kérdésekre:
Ø Miért van egy A1B1C1 háromszög az ABC háromszögnek?
Ø Mit jelent az A1B2C2 háromszög megegyezik az ABC háromszögrel?
Ø Miért egyezik meg a B2 pont a B1 ponttal?
Miért egyezik meg az A1C2 sugár az A1C1 sugárral?
Ø Miért egyezik meg a C2 pont a C1 ponttal?
6. Töltse ki a formanyomtatványokat és bizonyítsa az első tesztet a háromszög egyenlőségére.
Tétel. Ha két oldal és egy háromszög közötti szög egy másik háromszög _____________________________ értékével egyenlő, akkor ezek a háromszögek ___________;
Bizonyítsd be. # 8710; ABC = ________;
1) A tétel hipotéziseÐA =ÐH. Ezért az ABC háromszög
lehet alkalmazni a ___________________-ra úgy, hogy az A csúcs
kombinálódik a H csúccsal. Az AB és AC oldalakat az NK és a _______ sugarakra kell alkalmazni;
2) AB = _____ állapot esetén. AC = ______, ezért az AB oldala igazodik a ___________ párthoz. és a hangszóró oldalán - oldalán ______. különösen a B és ___ pontokat kombinálják. C és ____.
Ezért a felek _________________________;
3) Tehát az ABC és az NKR háromszögek teljesen egyesülnek, tehát ___________. A tétel bizonyított.
Problémák megoldása szájon át a rajzok szerint:
a) Bizonyítsuk be, hogy az ábrán látható háromszögek egyenlőek és írják be ezt az egyenlőséget (1.8 ábra).
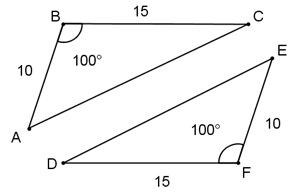

c) Keresse meg a CD-t (1.10 ábra).

Problémák megoldása a kész rajzokon: