Lecke - a származék alkalmazása a funkciók tanulmányozására a maximumra és a minimumra
A dokumentum rövid leírása:
A bemutató a lecke témájának bemutatásával kezdődik. A képernyőn megjelenik az y = f (x) függvény grafikonja. A grafikon azt mutatja, hogy a grafikonon nincs érintőpont az x = -1 pontnál, és x = 0 esetén az érintő vonal párhuzamos az X tengellyel, majd a függvény minimális meghatározását igazolják. Azt állítja, hogy az y = f (x) függvény minimális értéke x = x0. amelyhez létezik egy szomszédság, ahol f (x)> f (x0) érvényes a szomszédság minden pontjára. Az ábrán látható, hogy van egy körzet x = 0 - például (-0.5; 0.5), amelyben a környék összes értéke megfelel az f (x)> f (0) feltételnek. Megjegyzendő, hogy a funkció minimális értéke nem a legkisebb értéke, mivel a legkisebb értékről beszél, ha a definíció teljes tartományát figyelembe vesszük. Olyan gyakran fogunk.
Továbbá bemutatunk egy tételt, amelyben feltárjuk egy függvény és egy extremum származék közötti kapcsolatot. Meg kell jegyezni, hogy ha a függvény egy adott pontján van egy véglet, akkor a származék nem létezik, vagy nulla. Nyilvánvaló, hogy egy függvény vizsgálata során különös pontokat kell találni. A helyhez kötött és a kritikus pontok fogalma kerül bevezetésre. A helyhez kötött pontokat a függvénydefiníció tartományához tartozó pontokként definiálják, és a származék nulla. A kritikus pontok a definíciódomén pontjai, ahol a függvény folyamatos, de a származék nem létezik.
Megfontolandó egy példa, amelyben szükséges egy y = -x 2 + 4x-1 függvény grafikonjának összeállítása. A kvadratikus függvény grafikonjának ismeretében azonnal elmondhatjuk, hogy ennek a függvénynek a grafikája olyan parabola, amelynek ágai lefelé mutatnak, mivel a függvény vezető koefficiense negatív. A függvény maximális értéke a parabola csúcsa. A csúcs érintője az X tengellyel párhuzamos, így az y = 0 feltétel teljesül a csúcson. Megtaláljuk az y = (-x 2 + 4x-1) függvény deriváltját = -2x + 4. Az egyenlet -2x + 4 = 0 megoldásával x = 2 értéket kapunk. Az x = 2 pontnál az y = 3 függvény értéke. A talált (2; 3) pont a parabola csúcspontja. A parabola felépítéséhez két további szimmetrikus pontot választunk, például (0; -1) és (4; 0). Most könnyű ábrázolni a funkció grafikáját.
Továbbá bemutatjuk a 2. tételt, amelyben elegendő feltétel van a szélsőség számára. A tétel megállapítja, hogy egy y = f (x) függvény folyamatos az X intervallumon, amely ebben az intervallumban x = x0 kritikus pontot tartalmaz. igaz:
- ha a szomszédság a kritikus pont közelében van, ahol x<х0. f΄(x)<0, а для х>x0 f (x)> 0, akkor a pont a legkisebb a függvény;
- ha a szomszédság a kritikus pont közelében van, ahol x<х0. f΄(x)>0, és x> x0 f (x) <0, то данная точка есть максимумом функции;
- ha a szomszédság a kritikus pont közelében van, ahol a jel nem változik, amikor egy adott ponton áthalad, akkor nincs szélsőség.
A 2. példában meg kell találni a szélsőségeket, és rajzolnunk kell az y = 3x 4 -16x 3 + 24x 2 -11 függvény grafikonját. Először meghatározzuk az f (x) = (3h 4 -16x 3 + 24h 2-11) származékot. Az átalakulás után a származék f (x) = 12x (x-2) 2 formátumú. Az egyenlet megoldásai x = 0 és x = 2. Ezeket az állandó pontokat a számsor jelöli. A vonalon is megjegyezzük, hogy mi a függvény mindegyik kialakított intervallumban - növekszik vagy csökken. Nyilvánvaló, hogy a függvény csökken az intervallumon (-∞; 0), mivel a származék negatív értékeket vesz fel, és a (0; 2) és (2; + ∞) esetén a származék pozitív, a függvény növekszik. X = 0 esetén a függvény megváltoztatja az irányt a csökkenő értékről a növekvőre, ez a pont minimális, a származék jele nem változik x = 2-ben, így nincs túlsó határ. Egy minimális pontot találunk f (0) = -11. Ennek megfelelően az uinin. = -11.
Grafikon készítéséhez ismerni kell az álló, kritikus pontokat. Meghatározzuk a függvénynek a koordinátatengelyek metszéspontjait - ez (-1; 0), (1; 0). Figyelembe vesszük, hogy a funkció minimális értéke (-11; 0). És az álló pont (2; 5), ahol az érintő párhuzamos az X-vel, az inflexiós pont. Miután megtaláltuk a pontok több koordinátáját, létrehozunk egy függvény grafikát.
A tanulmány összefoglalásával algoritmust állítunk fel tetsz˝oleges y = f (x) folyamatos függvény vizsgálatára. Az algoritmus négy lépésből áll:
- keresse meg az f (x) származékot;
- kritikus, helyhez kötött pontok megtalálása;
- egypontos pontok kialakítása a koordináta vonalon - kritikus és helyhez kötött, jelezve a származék jeleit a keletkező réseken;
- következtetés a monotonitásról, a funkció végpontjairól.
Külön megjegyzést kell fűzni a koordináták egyenes vonalának jelölésére vonatkozó pontok szükségességéről, amelyek a p (x) / q (x) űrlap nevezőjét nullára változtatják. Jelezve, hogy ezek a pontok nem szélsőségesek.
A 3. példában meg kell vizsgálni az y = (x 2 -3) / (x 2 + 1) függvényt. A függvényt az algoritmus szerint vizsgáljuk. Először ott van a f (x) = ((x 2 -3) / (x 2 + 1)) derivált. A hányados deriváltjának megtalálására vonatkozó szabályt használva megtaláljuk az f (x) = 8x / (x2 + 1) származékot. A koordináta soron azt a pontot jelöljük, ahol a származék nulla - x = 0. Ezután rendezze el a származék jeleit a kialakult réseken. Nyilvánvaló, hogy az intervallumon (-∞; 0) a függvény csökken, és növeli a [0; + ∞) értéket. A grafikon tulajdonságai alapján az x = 0 pont a minimális függvény, ahol umin. = -3.
2. A végső függvények és a keresésük
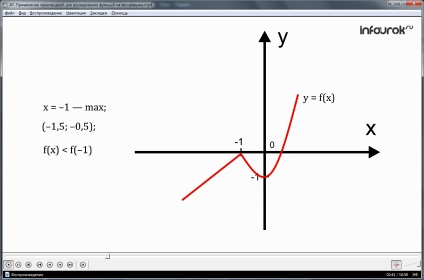
Vegyük figyelembe az 1. ábrán bemutatott függvény grafikonját. Ez a függvénynek nincs érintője az x = -1 pontban, és az x = 0 pontnál ez egyezik meg az y tengellyel (vagyis az x tengelyre merőlegesen).
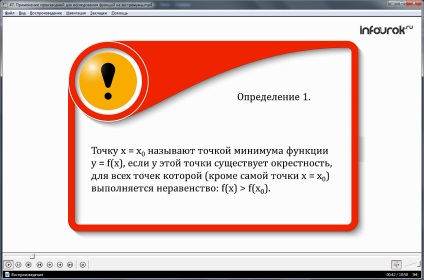
Definíció 1. Az x = x0 pontot az y = f (x) függvény minimális pontjaként nevezik, ha az adott pontnak van egy szomszédja minden pontra (kivéve x = x0 pontot), a következő egyenlőtlenség tartja:
Azaz a függvény, amelynek gráfja a 3. ábrán látható. 1, minimális pontja x = 0. Mivel egy adott pontban létezik egy szomszédság, például (-0.5; 0.5), minden pontnál, kivéve az x = 0, f (x)> f (0) hold értékeket. (ef X-től 0-nál nagyobb nulla)
A minimális ponton a függvény értéke ymin. (legalábbis minimum)
Megjegyzés. De ez az érték nem a funkció legkisebb értéke, mivel a legkisebb értéket a definíció minden tartományában figyelembe veszi, azaz a ymin gyakran eltér a yname-től. (a legkisebb)
Például, amelynek funkcióját a 2. ábrán mutatjuk be. 1, nem rendelkezik a legkisebb értékkel, de létezik a ymin (a minimális érték).
Definíció 2. Az x = x0 pontot az y = f (x) függvény maximális pontjának nevezzük, ha az adott pontnak van egy szomszédja minden pontra, kivéve az x = x0 pontot. a következő egyenlőtlenség: f (x)
Térjünk vissza az 1. ábrára, ez a függvény maximális pont x = -1. Mivel egy adott pontnál van egy szomszédság, például (-1.5, -0.5) minden pontnál, kivéve x = -1, f (x) pontot,
A függvény maximális értéke ymax. (iglok maximum)
Ne tévessze össze ezt az értéket a yanib-rel. (a legnagyobb összeg); a funkció legnagyobb értékével a definíció teljes területén.
Azt állíthatjuk, hogy a legnagyobb érték nincs jelen a vizsgált függvényben, létezik aymax (maximális érték).
A funkció minimális és maximális pontját a közös kifejezés - a végső pontok (a latin extremum - "extreme") egyesíti.
Tétel 1. Ha az y = f (x) függvénynek van egy végső pontja az x = x0 pontban. akkor ekkor a függvény deriváltja nulla vagy nem létezik.
Bemutatunk néhány további megjegyzést: egy függvény azon tartományának pontjai, amelyekben a függvény deriváltja egyenlő nullával, állóállapotúnak nevezzük. és annak a függvénynek a pontjai, ahol a függvény folyamatos, de a függvény nem létezik, kritikus.
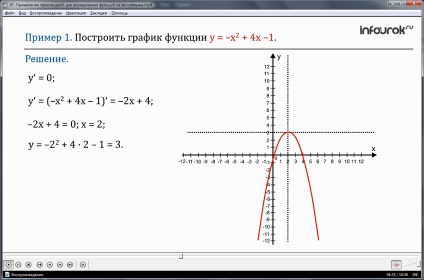
Példa 1. Hozzunk létre egy y = -x 2 + 4x-1 függvény grafikonját.
A megoldás. Tudja, hogy egy adott kvadratikus függvény görbéje egy parabola, a parabola ágak lefelé mutatnak, mivel a x 2 együttható negatív. Ebben az esetben azonban a parabola csúcspontja a függvény maximális pontja, a parabolának a csúcsán lévő érintője az x tengellyel párhuzamos, tehát az y '= 0 feltételnek teljesülnie kell a parabola csúcsán. (a szaggatott vonal nulla)
Van: y '= (-x2 + 4x-1)' = -2x + 4.
A származékot nullára kiegyenlítve megkapjuk a következőket: -2x + 4 = 0; x = 2.
A parabola-egyenletben található x érték helyettesítése:
y = -2 2 + 4 · 2 -1 = 3. (a játék három)
Így a parabola csúcspontja a (2; 3) pont, és az x tengely a parabola tengely. Ellenőrzési pontokként célszerű a (0; -1) és a
szimmetrikusan a parabola pont tengelyére (4; -1). Az 1. ábrán. 2, egy parabola - egy adott kvadratikus függvény grafikonját a talált három pontból állítjuk össze.
Tétel 2 (elégséges feltételek a végtaghoz). Tegyük fel, hogy az y = f (x) függvény folyamatos az X intervallumon, és van egy stacionárius vagy kritikus pontja x = x0 az intervallumon belül. majd:
a) ha ezen a ponton olyan szomszédság létezik, hogy x<х0 выполняется неравенствоf´(х) <0, а при х>x0 az egyenlőtlenség f (x)> 0, majd
b) ha ezen a ponton olyan szomszédság létezik, hogy x<х0 выполняется неравенствоf´(х)>0, és x> x0 esetén az egyenlőtlenség f (x)<0, то
c) ha ez a pont olyan szomszédsággal rendelkezik, hogy a származék jelei azonosak az x0 pont bal és jobb oldalán, akkor x = x0 pontban nincs szélsőség.
2. példa a) Keresse meg az y = 3x 4 -16x 3 + 24x 2 -11 függvény extremum pontját;
b) hozzon létre egy grafikont ennek a funkciónak.
Megoldás a) Keressük meg az adott függvény deriváltját: f '(x) = 12х 3 -48х 2 + 48х
f '(x) = 12x (x2 -4x + 4);
f '(x) = 12x (x-2) 2;
A származék az x = 0 és x = 2 pontokban eltűnik - ezek egy adott függvény két álló pontja. Az 1. ábrán. A 3. ábra vázlatosan jelzett származék jelek és viselkedését időközönként domain a funkció: az intervallum (-, 0) származék negatív, akkor a függvény csökken időközönként (0, 2) és a (2 +) - pozitív funkció növeli. A pont, x = 0, a függvény legkisebb pontja, és x = 2 nem extremum pont.
Az x = 0 minimális ponton f (0) = -11 (helyettesíti az x = 0 értéket
a függvény analitikus hozzárendelése), majd ymin = -11.
b) Egy függvénygrafikon létrehozásához ismerned kell a kritikus pontokat
grafika. Ezek a következők:
- a talált minimális érték (0; -1);
- álló x pont = 2; ezen a ponton f (x) = 3 · 2 4 -16 · 2 3 + 24 · 2 2 -11 = 5;
- metszéspontok a koordinátatengelyekkel; ebben a példában ez a pont (0; -11) már megtalálható, a gráf metszéspontja az y tengellyel. És újra: kitalálhatjuk, hogy f (1) = 0, tehát a gráf metszéspontja az x tengellyel megtalálható a pont (1; 0).
Tehát van egy minimális pont (0; -11), a gráf metszéspontja
Az x tengely a pont (1; 0) és az álló pont (2; 5). Ezen a ponton a függvény grafikonjának érintője vízszintes, de ez nem a végső pont, hanem az inflexiós pont.
A függvény grafikáját vázlatosan az 1. ábrán mutatjuk be. 4. Ne feledje, hogy még van
a grafikon metszéspontja az abszcissza tengellyel, de nem tudtuk megtalálni.
Tanultak általánosító algoritmusként.
A FOLYAMATOS FUNKCIÓ KUTATÁS ALGORITMUSA y = f (x) HA MONOTONITÁS ÉS EXTRÉMUMOK
1. Keresse meg a f '(x) származékot.
2. Keresse meg a helyhez kötött és kritikus pontokat.
3. Jelölje meg a számsoron lévő álló és kritikus pontokat, és határozza meg a származék jeleit a kapott intervallumokban.
4. A tételekre támaszkodva levonhatunk következtetéseket egy függvény monotonitásáról és végpontjairól.
Megjegyzés: Ha az adott funkció y = (y értéke Peh X osztva ku X), majd a számot sorban szükséges megjegyezni a pontok, ahol a nevező a q (x) értéke nulla, hogy meghatározza a származék karakterek. De ezek a pontok nem szélsőségesek.
6. példa: Az y = monotonicitás és extrema függvény vizsgálata.
A megoldás. Megjegyezzük, hogy a függvény mindenütt folyamatos, mivel a nevező bármelyik x pontnál nagyobb, mint nulla. A fenti algoritmust használjuk.
1) Lássuk egy adott függvény származékát:
(ef az X-ből való lökés egyenlő nyolc X-vel, osztva az X négyzet és egy összeg négyzetével).
2) A származék eltűnik az x = 0 pontokban, ez egy álló pont. A származék minden x, kritikus pontnál létezik, és a függvénynek nincsenek megszakítási pontjai.
3) Vegye figyelembe a 0 pontot a számsoron, és rendezze el a származék jeleit a kapott intervallumokban (5.
4) Következtetéseket vonunk le: a sugáron (-, 0) a függvény csökken, a [0, +] sugáron a függvény növekszik.
Továbbá x = 0 a minimális pont, ymin = -3 (a minimális érték mínusz három) (helyettesíti az x = 0 értéket az y = képletben).