Egy determinisztikus turing gép van
Determinisztikus Turing gép
Turing gép (MT) - elvont végrehajtó (absztrakt számítógép). Alan Turing 1936-ban javasolta az algoritmus fogalmának formalizálására.
A Turing-gép a véges automaton kiterjesztése, és az Egyház-Turing-értekezés szerint. utánozhat minden más előadóművészt (az átmeneti szabályok meghatározásával), amelyek valahogy végrehajtják a lépésenkénti számítási folyamatot, amelyben a számítás minden egyes lépése eléggé elemi.
Turing gép építése
A Turing gép mindkét irányból végtelenített szalagból áll (Turing gépek képesek, amelyeknek több végtelen szalagja van), cellákra osztva és egy vezérlő eszközzel. képes számos állam egyikében lenni. A vezérlőeszköz lehetséges állapotainak száma véges és pontosan meghatározott.
A vezérlőegység az átmeneti szabályok szerint működik. amelyek a Turing gép által alkalmazott algoritmust képviselik. Minden egyes átmeneti szabály arra utasítja a gépet, hogy az aktuális állapotban és az aktuális cellában megfigyelt szimbólumtól függően új szimbólumot írjon ebbe a cellába, menjen egy új állapotba, és mozgassa egy cella balra vagy jobbra. A Turing gép néhány állapotát terminálként lehet címkézni. és bármelyikre való átmenet jelenti a munka végét, az algoritmus megállítását.
A Turing-gépet determinisztikusnak hívják. ha az állam és a szalag szimbólum egyes kombinációja a táblázatban nem egynél több szabálynak felel meg. Ha van egy pár (szalag szimbólum - állapot), amelyre 2 vagy több utasítás van, akkor egy ilyen Turing gépet nondeterminisztikusnak neveznek.
A Turing gép leírása
Konkrét Turing-gép van beállítva felsorolja az ábécé halmaz elemeit egy, a beállított Q államok és egy sor szabályt, amellyel a gép működik. Ezek formájában :. Qi aj → qi1 Aj1 dk (ha a fej az állam qi és a megfigyelt sejt írott levelében aj a fej mozog az állami qi1 cella helyett AJ rögzített Aj1 fej teszi mozgás dk, amelynek három lehetőség ....: balra (L), jobbra (R) a cellába, hogy a helyén maradjon (H). Minden lehetséges konfigurációhoz
Példa egy Turing gépre
Íme egy példa a MT számok szorzására egy unary számrendszerben. A gép az alábbi szabályok szerint működik:
A protokoll meghatározza az MT kezdő és záró állapotait, a szalagon lévő kezdeti konfigurációt és a gépfej helyét (aláhúzott szimbólum).
Turing teljessége
Azt mondhatjuk, hogy a Turing gép egy egyszerű, lineáris memóriával rendelkező számítógép, amely a formális szabályok szerint átalakítja a bemeneti adatokat egy elemi műveletsorral. Alapvető művelet az, hogy az akció csak egy kis adatdarabot változtat a memóriában (a Turing-gép esetében csak egy cella), és a lehetséges műveletek száma véges. Annak ellenére, hogy egyszerűen a Turing gép, lehetséges minden olyan számítást kiszámítani rajta, amely kiszámítható bármely más gépen, amely számításokat végez az elemi műveletek sorozatával. Ezt a tulajdonságot teljességnek nevezik.
Az egyik természetes módja annak bizonyítására, hogy az egyik gépen megvalósítható számítási algoritmusok végrehajthatók a másik oldalon, az első gép szimulációja a másodikban.
Amint azt már említettük, a Turing-gépen az átmeneti szabályok beállításával szimulálhatják az összes többi előadót, akik valahogy megvalósítják a lépésenkénti számítások folyamatát, amelyben a számítás minden egyes lépése eléggé elemi.
A Turing gépen szimulálhatja a Post gépét. a normál Markov algoritmusok és minden olyan program, melyet hétköznapi számítógépeken alakítanak ki, hogy valamilyen algoritmust átalakítanak a bemeneti adatok kimenetére. Viszont különböző absztrakt művészek utánozhatják a Turing gépet. Az előadóművészeket, amelyekre ez lehetséges, a teljes Turing (Turing teljes).
Rendelkeznek olyan számítógépekkel, amelyek utánozzák a Turing gép munkáját. De meg kell jegyezni, hogy a szimuláció nem teljes, mivel van egy Turing-gép absztrakt végtelenített szalag. Végtelenített szalag az adatokat lehetetlen teljesen szimulálják a számítógép véges memória (összesen számítógép memóriájában - RAM, merevlemez, a különböző külső adathordozóra, regiszterek, és a CPU cache, stb -. Legyen nagyon nagy, de mégis, mindig véges).
A Turing gép változatai
A Turing gép modellje kiterjesztéseket tesz lehetővé. A Turing-gépek tetszőleges számú szalaggal és többdimenziós szalaggal különféle korlátokkal bírhatnak. Mindazonáltal ezek a gépek Turingben teljesek, és egy hagyományos Turing gép által modellezett
Turing gép egy félig végtelen szalagon dolgozik
Az ilyen információk példájaként vegye figyelembe a következő tételt: Minden Turing-gépen létezik egy egyenértékű Turing-gép, amely félig végtelen szalagon működik.
Tekintsük a Yu.G. Karpov a "The theory of Automata" című könyvében. Ennek a tételnek a bizonyítása konstruktív, azaz. adunk egy olyan algoritmust, amellyel egy Turing-gépet a Turing-géphez tervezhetünk. Először, önkényesen számozzuk meg az MT munkasáv celláit, azaz határozza meg az új információ helyét a kazettán:
Ezután újraszámozzuk a cellákat, és feltételezzük, hogy a "*" szimbólum nem szerepel az MT szótárban:
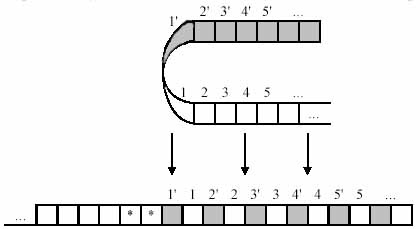
Végül, változtassa meg a Turing-gép, megduplázva a száma annak államok, és a változás a váltás író-olvasó fej úgy, hogy az egyik csoport a gép állapotát egyenértékű lenne munkáját az árnyékolt terület, míg a másik csoport az állam gép fog működni, mint az eredeti gép működik egy árnyékos helyen. Ha az MT műveletben megjelenik a "*" szimbólum, akkor a read-write fej elérte a zónahatárt:
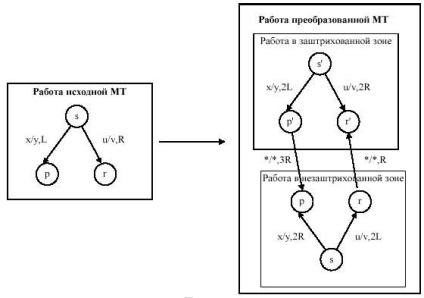
Az új Turing gép kezdeti állapota az egyik vagy a másik zónában van beállítva, attól függően, hogy az eredeti konfigurációban lévő olvasás-írófej hol található a forrásszalag egy részén. Nyilvánvaló, hogy az egyenértékű Turing-szalag szalagját nem használjuk a "*" határolójelzők bal oldalán.