Az olimpiai győztesek társulása
Ma a vektordiagram-módszer egy kissé nem szabványos és néha lényegesen egyszerűbb megoldását vesszük figyelembe.
A kinematikai egyenleteket egy jó fizikai tankönyvben vektor formában adják meg. De megoldani a problémákat, általában a koordináták tengelyein levő vetítésekre írjuk őket, és egy elegáns egyenlet helyett egy nagy rendszert kapunk. Ez a legegyszerűbb esetekben vagy időigényes feladatokban hasznos. A problémák kiterjedt csoportja, ahol ez a megközelítés nem optimális, és a geometriai leírás segíthet. Mivel ezek a problémák "helyes" megoldást kínálnak, a megoldás nagyon szép és elég rövidnek tűnik, gyakran különböző szintű olimpiákon jelenik meg. Figyelembe kell venni a testek szabad hulláma eseteit a gravitációs mezőben a levegőellenállás hiányában. Szekvenciálisan ez képviselhető:
A kinematika alapvető összefüggései vektoros formában írva:
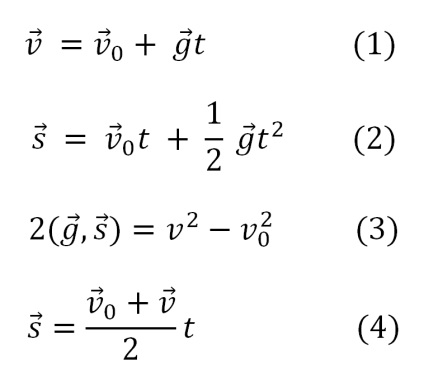
A módszer két kulcsfontosságú vektor háromszöget használ: sebességeket és eltolódásokat:
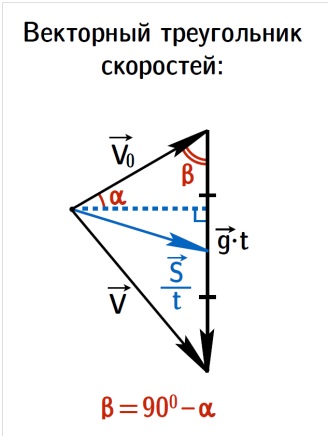
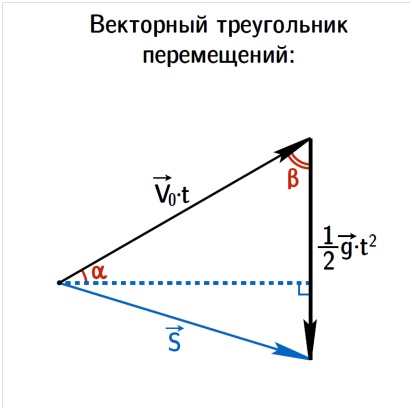
Megépítjük a vektor sebesség háromszöget:
A v0 vektort egy bizonyos α kezdeti szöggel elhalasztjuk a horizontig, végéig a g t vektort lefelé irányítjuk. E két vektor összege az (1) egyenlet szerint adja meg a v vektort.
Egy vektor eltolódásos háromszög megépítése érdekében a v0 v vektort párhuzamosan a v0-val párhuzamozzuk. Végül hozzáadunk egy vektort. A (2) egyenletnek megfelelően a vektort s összegekként kapjuk meg.
Nézzük meg jobban az ábrát: a függőleges oldalon leeresztett magasság a test elmozdulása vízszintesen vagy, ahogy általában nevezik, az L. a hullámtér tartománya - mint korábban, a vízszintes elhúzás szöge. Az a szöggel ellentétes cathetus a függőleges elmozdulás h.
Térjünk vissza a sebesség háromszögbe. A (2) bekezdésből következik:
Eszközök, - az elmozdulás háromszög függőleges oldalán húzott középérték. Ez megfelel a (4) egyenletnek, ahol a háromszögnek a sebességvektorokon felépített középértéke megfelel.
A hasonlóság szempontjairól és két háromszög összehasonlításáról azt állapítjuk meg, hogy az ugyanarra az oldalra húzott magasság egyenlő, és a jobb felső háromszög katéte az α szöggel ellentétes.
Így sikerült két kulcsfontosságú háromszöget összekapcsolni, és geometrikusan kifejteni a kinematika alapvető viszonyait. Nézzünk ki néhány konkrét esetet és a háromszögek kialakuló tulajdonságait:
Ha v0islv. akkor a sebesség háromszög négyszög alakul ki, ami azt jelenti, hogy a medián a hypotenuse fele.
Ha v0islv. akkor a sebesség háromszög két izoelettű háromszögből áll, ezért a v0 sebesség a függőleges és a vektor által alkotott szögfelező mentén irányul.
A sebesség háromszög területe a következőképpen fejezhető ki:.
Példaként elemezzük a problémát:
Egy kő a talajról a szögben a horizont felé dob. Egy τ idő elteltével a domb felszínére esik, amelynek sebessége a kezdeti értékre merőleges. Mi a távolság a dobás pontjai és a leszállás között? A levegővel szembeni ellenállást elhanyagolják.
Tekintsünk egy sebesség háromszöget. A repülések kezdetén és végén merőlegesek a sebességek ⇒ van egy derékszögű háromszög. A medián a hypotenuse fele ⇒.
Javasoljuk, hogy megoldja a következő feladatokat (a források felsorolása a szám mellett).
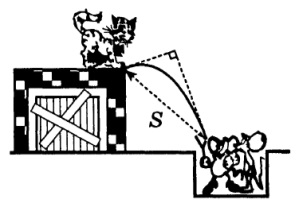
1. A kecske, Slobodian 9.62
Cat Leopold a tető szélén ült. Két csintalan kis egér egy lövedékből kővel lőtte le. Az ív leíró kő a macska lábánál τ = 1 c-ra esett. Milyen messze volt az egér a Leopold macskától, ha a lövedék idején és a bukás idején a kő sebességvektorai egymásra merőlegesek voltak?
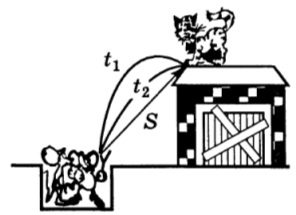
2. A kecske, Slobodyanin 9.71
Leopold macskája a pajta tetejének szélén állt. Két csintalan kis egér egy lövedékből kővel lőtte le. Azonban, kő, amely leírja az ív, t1 = 1,2 és rugalmasan tükrözi a ferde lejtőn a tető a fészer a nagyon macska karmai keresztül t2 = 1,0, hogy elérje az egér mancs shooter. Milyen távolságban volt az egerek a Leopold macska?
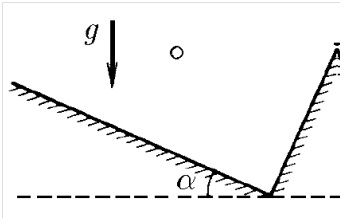
3. Savchenko 1.3.17
Egy téglalap alakú dobozban, amely az alsó és a jobb falhoz támaszkodik, egy labda ugrik egy és ugyanolyan módon oda-vissza. Az alj és a fal közötti ütközések közötti időtartam Δt. A doboz alja egy α szöget alkot a horizonttal. Keresse meg a labda sebességét közvetlenül a lökések után.
Savchenko 1.3.10
A kacsa vízszintes egyenes vonal mentén állandó sebességgel u. Egy tapasztalatlan "vadász" vetette a kő belsejébe, és a dobást elővigyázás nélkül tették, i.e. az öntés pillanatában a kő sebessége pontosan a kacsa felé irányult, a szögben a horizontig. Mennyire magasodott a kacsa, ha a kő belekeveredett?