A megrendelések megrendelésének ütemterve az áruk, munkák, szolgáltatások igényeinek kielégítésére
LESSON: "VEKTOR BOMÁNYOSÍTÁS KÉT NON-COLLINAR VEKTOROKBAN"
Tárgy: Vektor elválasztása két nem-kolináris vektorra vonatkozóan
Osztály: 9. fokozat
Tanár:. igazgatóhelyettes az oktatási munkákért. a matematika és a számítástechnika tanára.
Oktatási intézmény: a Kemerovo régió Shura középiskola
Mostani város: Кемеровская область
Ismerje meg a kollineáris vektorok formulációját és bizonyítékát, valamint a két nem kolináris vektor tágulási tételét;
A problémák megoldása a megszerzett tudás alkalmazásával.
I. Szervezési pillanat: nevezze meg a lecke célkitűzéseit.
III Új anyag magyarázata:
1. Vektor kiterjesztése két nem-kolináris vektorra.
A problémák megoldásakor gyakran szükségessé válik egy vektor kifejeződése a már megadott vektorokon keresztül. Egy ilyen műveletet vektor meghosszabbításának nevezünk a nem kolináris vektorok vonatkozásában.
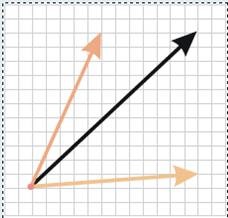
2. A kollineáris vektorok lemma.
A lemma egy segédkifejezés, amellyel bizonyítható a következő tétel vagy több tétel.
Tétel: Ha a vektorok mind kollineárisak, mind pedig # 61625; 0, akkor létezik olyan k szám, hogy = k.
Mivel a vizsgált vektorok kollineárisak hipotézis szerint, ugyanazok az irányok lehetnek. Tekintsünk két olyan esetet, amikor a vektorok mindkettõ irányított és ellenõrzõ irányba mutatnak.
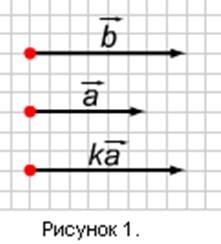
1). Vegyünk egy számot. Mivel k 3, a k vektorok és az egyirányúak (1. ábra). Emellett ezek hossza egyenlő: k1 k1 = k1 1 k1 = k1 1 = k1 1. Ezért = k
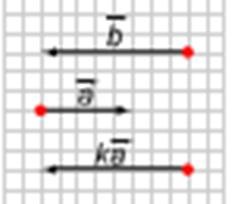
3. Egy vektor bontására vonatkozó tétel két nem-kolináris vektorra vonatkozóan.
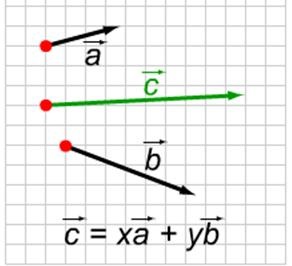
Hagyja, hogy ne legyen hollo-mális vektor, a vektor a formában jelenik meg
= x + y, ahol x és y bizonyos számok. Általában azt mondják, hogy a vektor vektorokba bomlik és. Az x és y számokat kiterjesztési együtthatóknak nevezzük.
Két lehetséges eset van:
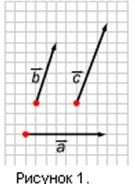
2) A vektor nem kötődik sem a vektorhoz, sem a vektorhoz. Megjegyezzük az O pontot, és elhalasztjuk a vektorokat =, =, = (2. ábra).
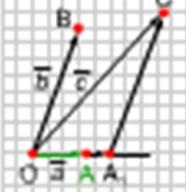
Most bizonyítjuk, hogy az expanzió x és y együtthatói egyedileg vannak meghatározva. Tegyük fel, hogy az x + y bomlás mellett egy másik bomlás is van = x1 + y1. A második egyenlőség elvonását az elsőtől és a vektorok cselekvési szabályainak használatával kapjuk = (x-x1) + (y-y1). Ez az egyenlőség csak akkor teljesíthető, ha az x-x1 és az y-y1 együttható nulla. Valójában, ha feltételezzük, hogy x-x1 0 0, akkor az egyenlõségbõl az = -, és így a vektorok kollineárisak. Ez azonban ellentmond a tétel hipotézisének. Következésképpen x-x1 = 0 és y-y1 = 0, ahonnan x = x1 és y = y1. Ez azt jelenti, hogy a vektor együtthatói egyedileg vannak meghatározva. A tétel bizonyított.
1. A lemma az egy vagy több tétel bizonyításánál használt segédkifejezés.
2. Lemma (collineáris vektorokon). Ha a vektorok mind kollineárisak, mind a # 0 vektor, akkor létezik olyan k szám, hogy k = k
3. Adjunk hacsak nem kollineáris vektorokat, a vektort formában ábrázoljuk
= x + y, ahol x és y bizonyos számok. Általában azt mondják, hogy a vektor vektorokba bomlik és. Az x és y számokat kiterjesztési együtthatóknak nevezzük.
4. Tétel: Bármelyik vektor két nem hengeres vektorra bontható, és a tágulás együtthatói egyedileg vannak meghatározva.
IV. A megszerzett tudás konszolidációja:
1. Az ABCD paralelogramma átlói metszenek az O ponton. Expresszük a vektort a vektorokon keresztül.
4. № 000 (a, d). A parallelogram átlói metszenek az O ponton, és M az AO szegmens középpontja. Találd meg, ha lehetséges, olyan számot, hogy az egyenlőség: = k, = k
5. Adott egy tetszőleges háromszög ABC az AD median. Keresse meg, hogy a vektor hogyan fejeződik ki a vektorok és.
V. Összefoglalva.
VI. Hozzárendelés a házhoz: tétel 86, № 000 (û, г), 912 2,3 oszlop), 916 (в, г)