A kettős integrál definíciója
A kettős integrál definíciója
Hagyja, hogy a sík $ \ mathbf> $ egy korlátos zárt régió $ \ mathbf> $ a szakaszonként sima határ, és hagyja, hogy a területen $ \ mathbf> $ funkciójának meghatározása $ \ mathbf> (\ mathbf> $, $ \ mathbf>) $ .
Osztjuk a régió $ \ mathbf> $ önkényesen $ \ mathbf> $ aldomain $ \ mathbf> _ $, $ \ mathbf> _ $, $ \ mathbf> _ ,, \ mathbf> _ $ ,. A $ \ mathbf> (\ mathbf> _) $ szimbólum a $ \ mathbf> _ $ tartomány tartományát jelöli; szimbólum $ diam (\ mathbf>) $ ide, és továbbra is a legnagyobb távolság két pont között területéhez tartozó $ \ mathbf> $: $$ diam (D) = \ mathop \ limits_ \ Rho (p_1, P_2); $$ jel $ d $ jelöli a legnagyobb átmérője $ \ mathbf> _ $: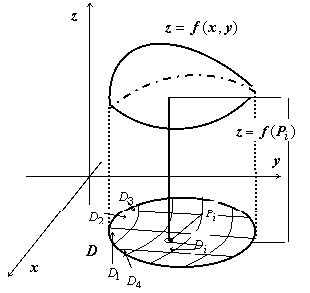
Ha létezik egy korlátozás az Integrált Összegek sorozatára vonatkozóan
$ D = \ mathop \ limits_ diam (D_i) \ 0 $, nem függ sem az eljárás partíciózását mező $ \ mathbf> $ egy aldomain $ \ mathbf> _ $, sem a választott pont $ \ mathbf> _ $, akkor a függvény $ \ mathbf> (\ mathbf> $, $ \ mathbf>) $ nevezik integrálható mező $ \ mathbf> $, de az értéke ez a határ az úgynevezett kettős integrál függvény $ \ mathbf> (\ mathbf> $, $ \ mathbf>) $ a mező $ \ mathbf> $ és jelöljük $ \ iint \ limits_D $.Ha a festék értéke $ \ mathbf> (\ mathbf>) $ a koordinátáit $ \ mathbf> $, és $ \ mathbf> $ a $ \ mathbf> = \ mathbf> $ szerezze egyéb megjelölése kettős integrál: $ \ iint \ limit_D $. Szóval, röviden,A kettős integrál létezési tétele
Ha a $ \ mathbf> (\ mathbf>, \ mathbf>) $ integrandum folytonos a $ \ mathbf> $ tartományban, akkor integrálható ezen a tartományon.
A kettős integrál geometriai jelentése. Az integrált összeg minden egyes kifejezésének geometriai jelentése
A geometriai szempontból az integrál összeg a $ s (D _) $ és $ f (P_i) $ alapú hengerek mennyiségének összege.
Ha $ f (x, y) \ geqslant 0 $, akkor a $ f (P_i) \ cdot s (D_i) $ - a kötet egy egyenes henger egy bázissal $ \ mathbf> _ $ magasság $ \ mathbf> (\ mathbf> _) $ ; Az összes szerves összeg $ \ sum \ limits_ ^ n $ - az összeget a henger kötetek, azaz a kötet egy test lépésben - a lépcső magassága, a fenti a aldomain $ \ mathbf> _ $, egyenlő $ \ mathbf> (\ mathbf> _) $. Amikor a $ d = \ mathop \ limits_ diam (D_i) \ 0 $, ez a lépés a test egyre közelebb az egyetlen ábrán látható teste, korlátozott alsó területen a $ \ mathbf> $, felső - felülete $ \ mathbf> = \ mathbf> ( \ mathbf> $, $ \ mathbf>) $, a hengeres oldalsó felülete mentén, amely a határ az $ \ mathbf> $, a hossztengellyel párhuzamos, és a generátorok $ \ mathbf> $. A kettős integrál $ \ iint \ limits_D $ megegyezik a test mennyiségével.Olvassa el:
Az első fajta felületi integrációja és tulajdonságai
Az első típusú görbe vonalú integrál mechanikus alkalmazása
Az eltérés invariáns definíciója
A hármas integrál mechanikus alkalmazása
Menj a tartalomjegyzékhez $ \ Rightarrow \ Rightarrow \ Rightarrow $