Self-help windows xp, Microsoft Office, juhar, photoshop, corel draw, matematikai programok,

A 3D grafikák, amelyeket 3D-s grafikának is neveznek, az ekvivalens elemek háromdimenziós képét ábrázolják, amelyek két változó funkciói vagy paraméterek által meghatározott objektumok koordinátái. Ez a szakasz a háromdimenziós grafikonok kialakításának számos módját ismerteti, kezdve egyszerű kontúrgrafikonoktól és a funkcionális színű felületek és ábrák grafikonjaival.

Kontúrgrafikonok létrehozása

A kontúrt ábrázoló grafikák vagy egyenlő magasságú vonalak grafikonjai sík felületek megjelenítésére szolgálnak. Ezek alkalmasak arra, hogy a grafikonon belül minden funkciók végét észleljék. Ilyen grafikonok a felület metszésvonalai szomszédos vízszintes síkokkal párhuzamosak egymással. Gyakran használják a térképészetben.

A kontúrgrafikonok kialakításának főbb funkciói és irányelvei a következők:

• ContourPlot [f ,,] - egy f kontúrpléteget generál x és y függvényeként;
• ContourGraphics [array] - a tömb tömb kontúrterve;
• ListContourPlot [tömb] - kontúrpárt alkot egy magassági értéktartományból.

Ezek a funkciók elegendőek az ilyen típusú monokróm grafikonok elkészítéséhez.

A ContourPlot grafikus funkció lehetőségeinek vezérlésére olyan opciókat használnak, amelyek teljes listáját a [ContourGraphics] Opciók parancs mutatja. A korábban megfontolt lehetőségek mellett a következőket használják:

• ColorFunction - meghatározza a területek színét a vonalak között;
• Kontúrok - meghatározza a kontúrvonalak számát;
• ContourLines - meghatározza az explicit (explicit) kontúrvonalak rajzát;
• ContourShading - meghatározza a kontúrvonalak közötti terület árnyékolását;
• ContourSmoothing - a kontúrvonalak simítása;
• ContourStyle - meghatározza a rajzolt vonalak stílusát a kontúrgrafikonokhoz;
• MeshRange - állítja be az x- és y-koordináták régióit.

A 8.15. Ábra a vonalak közötti köztes régiók színének ábrázolását ábrázolja. A színezést a ColorFunction-> Hue opció biztosítja. A ContourSmoothing -> True beállítja a kontúrvonalak simítását.

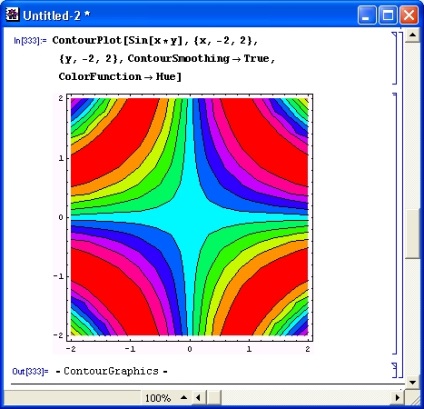
Ábra. 8.15. A felszíni bűn (x y) kontúrterülete, a szürke árnyalatú egyenletű vonalak közötti sötétítéssel

A következő példa (8.16. Ábra) szemlélteti a ContourShading opció hatékonyságát. Ha az értékét False értékre állítja, akkor a vonalak közötti tér kitöltése hiányzik. Így ebben az esetben csak egyenlő szintvonalak vannak kialakítva.

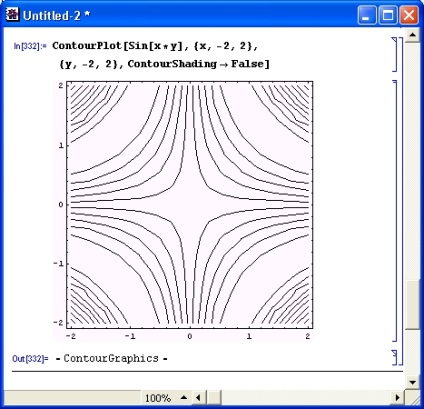
Ábra. 8.16. Kontúrgörbe, amelyet csak egyenlő szintvonalak képviselnek

Néha a grafikon sokkal nyilvánvalóbb, ha eltávolítja a kontúrvonalak építését, de hagyja el a régiókat árnyékolva a vonalak között. A grafikon ilyen változata előnyösebb, ha minőségi képet kell megfigyelni. Egy ilyen gráf elkészítéséhez a ContourLine-> False opciót kell használni (lásd 8.17. Ábra).

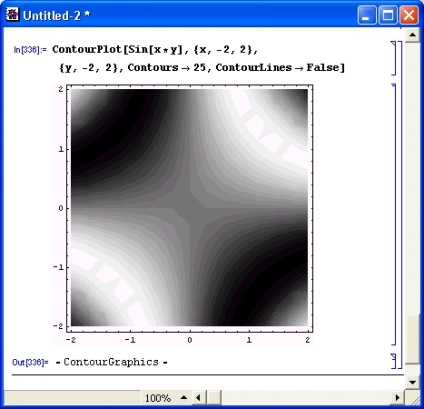
Ábra. 8.17. Egy egyenlő sík nélküli csúcsok

Sűrűségtáblák építése

A közeg sűrűségét két f (x, y) változó függvényében írhatjuk le. A sűrűségi grafikonok ábrázolásához a következő grafikus függvényeket használjuk:

• DensityGraphics [array] - a sűrűségi grafikon ábrázolása;
• SűrűségPlot [f ,,] - a f sűrűség grafikonja az x és y függvényeként;
• ListDensityPlot [tömb] - egy sűrűségi gráfot képez egy magassági értéktartományból.

Ezekkel a funkciókkal sok (többnyire már figyelembe vett) opciót használnak. A listájuk az Opciók funkció segítségével érhető el.

Külsőleg a sűrűségi grafikon hasonló a kontúrtervhez. Ugyanakkor jellemző arra, hogy elválasztja az elemi régiókat (egyenlő sűrűséggel) négyzetek formájában (8.18. Ábra).

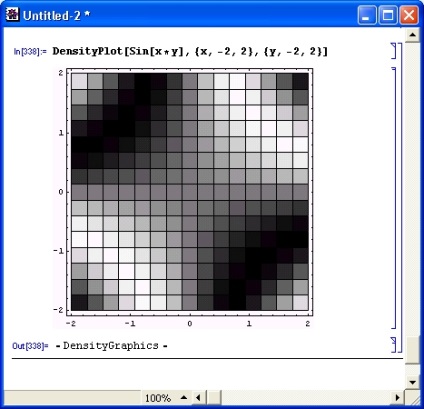
Ábra. 8.18. A sűrűség grafikonja

A felületek ábrázolása - a Plot 3D funkció

A két változó függvénye z = f (x, y) a térben háromdimenziós felületet vagy ábrát alkot. Építésükhöz egy koordináta-rendszert kell használnunk három koordináta-tengellyel: x, y és z. Mivel a kijelző képernyője lapos, sőt, a számok nagy része csak szimulált - jól ismert módszert alkalmaz a háromdimenziós ábrák vizualizálásához axonometrikus vetítéssel.

Ahelyett, hogy egy szám összes pontját megépítenénk, általában egy drótváz modellt készítünk, amely az alak vágási vonalát tartalmazza kölcsönösen merőleges síkok mentén. Ennek eredményeképpen az ábrát görbe vonalú négyszögek sorozataként ábrázoltuk. Annak érdekében, hogy az ábra természetesbb legyen, a láthatatlan keretvonalak eltávolítására szolgáló algoritmust és a négyszögek funkcionális festését használják az ábrán az oldalirányú megvilágítás szimulálására.

A háromdimenziós felületek grafikonjának ábrázolásához a Plot 3D fő grafikai funkciót használjuk:

• Plot3D [f,] - az x és y változók f függvényének háromdimenziós diagramja;
• Plot3D [,,] - egy háromdimenziós grafikont hoz létre, amelyben a felület magassága határozza meg az f paramétert, és az árnyékolás az s paraméter.

Az 1. ábrán. A 8.19. Ábrán példaként bemutatunk egy olyan felületet, amelyet két, y (xy) változó függvényében írunk le az x és y változókra, amelyek értéke -3 és 3 között változik. A felület funkcionális színű, négyszögletes cellákkal rendelkező keretként van kialakítva. Minden beállítás alapértelmezés szerint be van állítva.

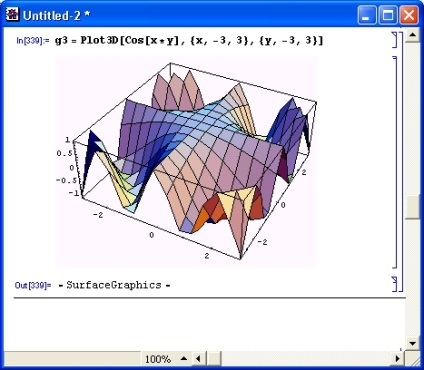
Ábra. 8.19. Példa a felületi cos (xy) Plott3D függvény ábrázolására az alapértelmezett beállításokkal

Ezt az ütemtervet a módosítások bemutatásának kiindulópontjaként fogják tekinteni.

3D grafikus opciók és irányelvek

A háromdimenziós grafikonok módosításához számos opció és irányelv használható, amelyek listáját a függelék tartalmazza. Használatuk lehetővé teszi számos különböző típusú grafikon felépítését, még akkor is, ha azonos felületet ad meg. Példaként tekintse meg a dokumentum egyes képkockáit, amelyek bemutatják az opciók hatását a háromdimenziós matematikai felület megjelenésére.

Az 1. ábrán. A 8.20. Ábrán az eredeti felület látható (lásd a 8.19. Ábrát), amelyet a PlotPoint-> 50 opcióval készítettünk. Ez azt jelenti, hogy az egyes tengelyek felszínét 50 részre osztják (az eredeti grafikonon alapértelmezés szerint a 10 részre osztás). A függőleges skála automatikusan úgy van beállítva, hogy a felület minden emelkedése ne legyen korlátozva.

Az 1. ábrán. A 8.21 ábra ugyanazt a felületet mutatja, mint a PlotRange-> opciót, amely a felület tetejét vágja (0,5 pont felett lévő pontok). A felületi grafikon jelentősen megváltozik (összehasonlítás a 8.20. Ábrával).

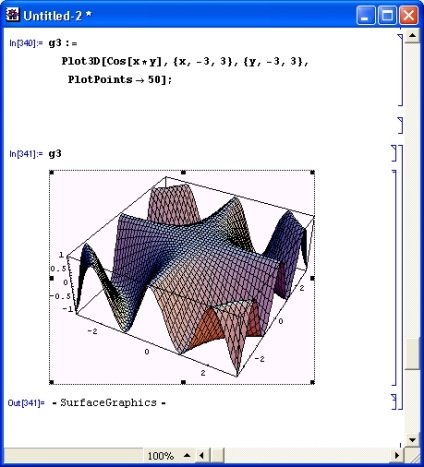
Ábra. 8.20. Az 1. ábra felülete 8.19 nagyszámú cellával

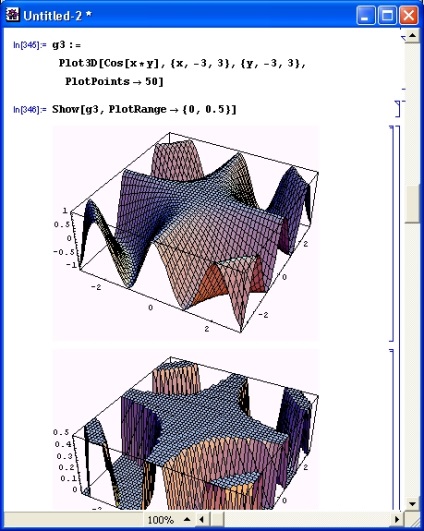
Ábra. 8.21. Matematikai felület vágott felülettel

A Boxed -> False opció eltávolítja azokat a határoló dobozokat, amelyek a "doboz" formáját alkotják, amelybe a felépített 3D felület illeszkedik (lásd a 8.22. Ábrát). Csak a koordinátatengelyek maradnak.

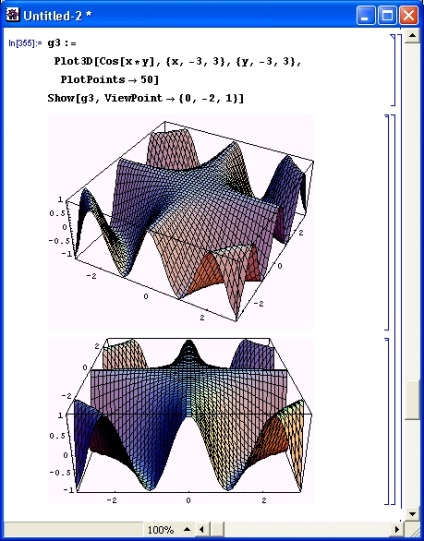
A Nézet opció lehetővé teszi a perspektív leképezést az építésbe és változtassa meg a szögeket, amelyek alatt az ábrán látható. A 8.23. Ábra szemlélteti az opció használatát.

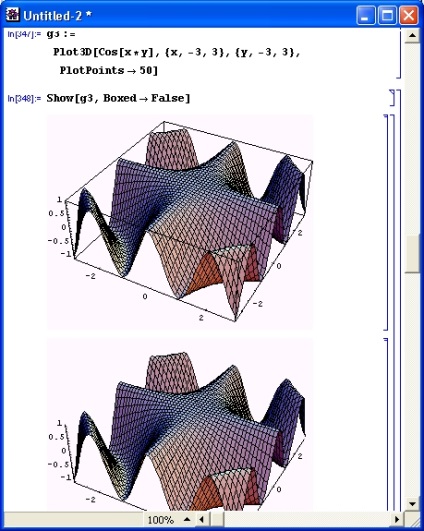
Ábra. 8.22. A háromdimenziós felület megalkotása korlátozó "doboz" nélkül

Ábra. 8.23. A matematikai felület perspektivikusan van kialakítva

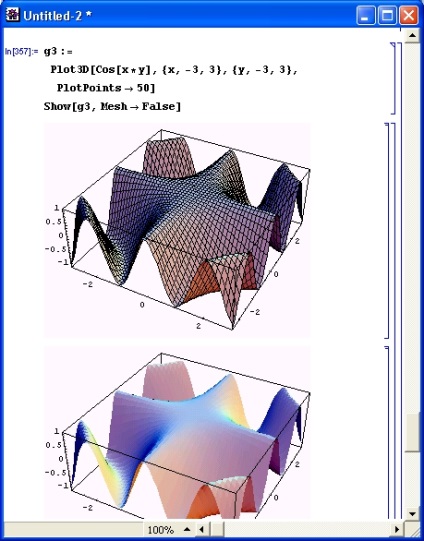
Option Mesh -> False lehetővé teszi, hogy törölje az ábra vázának vonalát. Gyakran ez adja az ábrát egy természetes megjelenésnek (8.24. Ábra) - általában ilyen számokat látunk a drótvázas vonalak nélkül.

Számos esetben éppen ellenkezőleg, a hasított testek fontos információkat hordoznak. A rendszer kétféleképpen képes háromdimenziós felületek vázára - algoritmussal és anélkül, hogy láthatatlan vonalakat eltávolítanának. A 8.25. Ábra az építmény eredményét mutatja a láthatatlan vonalak eltávolítására szolgáló algoritmussal. Látható, hogy ebben az esetben a felület funkcionális árnyékolás nélkül is esztétikailag kellemesnek tűnik.

Ábra. 8.24. A matematikai felület a csontváz elvont vonalaiból

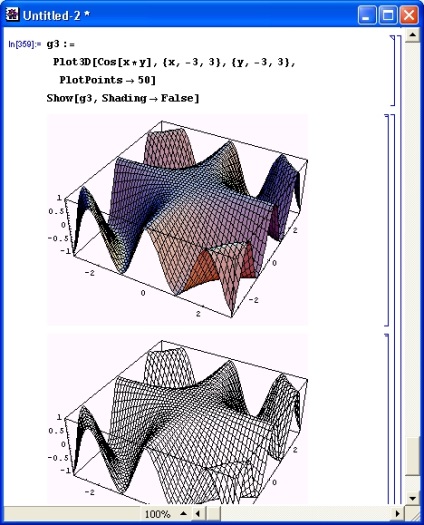
Ábra. 8.25. A matematikai felület keretének kialakítása a láthatatlan vonalak eltávolítására szolgáló algoritmussal

Az 1. ábrán. A 8.26. Ábra mutatja a keret építését láthatatlan vonalak eltávolítása nélkül. Ez a fajta matematikai felület, ha elképzelhető, hogy a térben lógó vékony vezetékekből épül fel. Ez további információt ad a térbeli alakról, de esztétikailag rosszabbnak tűnik, mint a láthatatlan keretvonalak eltávolítására szolgáló algoritmussal konstruált alak.

Így, mint korábban, az opciók használata megkönnyíti a grafikonok jellegének és típusának ellenőrzését, így egy adott alkalmazás számára megfelelő nézetet biztosít. Az 1. ábrán. A 8.27. Ábra egy háromdimenziós grafikon kialakítását mutatja, több lehetőség egyidejű alkalmazásával.

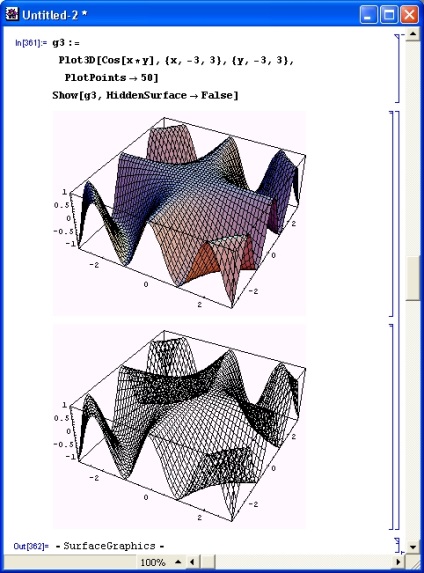
Ric. 8.26. A matematikai felület keretének megépítése algoritmussal a láthatatlan vonalak eltávolítására

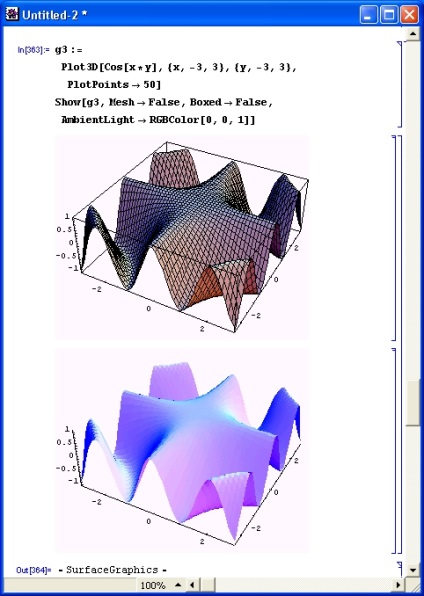
Ric. 8.27. Példa egy háromdimenziós grafikon létrehozására több lehetőséggel

A legrajzolódóbb példákkal szemléltetett példák azt mutatják, hogy a grafika milyen egyszerűen módosítható különböző lehetőségek segítségével. Természetesen sok lehetőség van más módosításokra, amelyeket a felhasználó egyedül megpróbálhat.

Az alkalmazás ebbe a leckébe szánt részében több további irányelv és lehetőség van a 3D grafikákra. Segítségükkel kibővítheti a rajzolás lehetőségeit. Az olvasó javasolja, hogy különböző felületek grafikonjait egymástól függetlenül készítsék el különböző lehetőségekkel.

Grafikus funkció ListPlot3D

Gyakran a háromdimenziós felületet egy magassági tömb (applikátor) határozza meg. Ebben az esetben egy grafikon létrehozásához használja a ListPlotSD grafikus függvényt:

• ListPlot3D [array] - felépít egy háromdimenziós gráfot a felülettel, amelyet egy magassági tömb képvisel;
• ListPlot3D [array, shades] - gráfot hoz létre, hogy a felület minden egyes eleme árnyékolva legyen (árnyékolt) az árnyalatok specifikációjának megfelelően.

A Plot csatlakozás opcionális opció a ListPlot számára, jelezve, hogy a diagramon megjelölt pontokat egy sorral összekapcsolja-e.

A ListPlotSD funkció használatának egyik példája az 1. ábrán látható. 8.28. A grafikon a tS táblázatból származó adatokból épül fel, amely a cos app funkció (xy) függvényében leírja a felületi applikáció értékét.

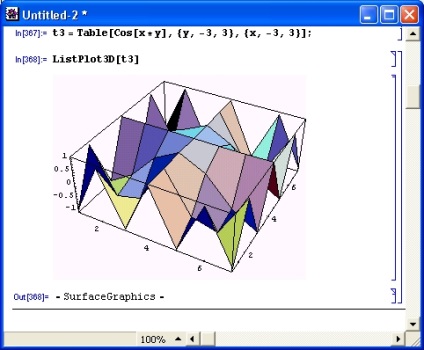
Ábra. 8.28. Példa a ListPlotSD függvény használatára

Az ebben a fejezetben leírt grafikus funkciók mellett azok opcióival, irányelveivel és primitívjeivel nagyszámú háromdimenziós grafikon létrehozható. Azonban sok ilyen grafikát hozhat létre a Graphics kiterjesztés csomagban található további funkciók segítségével. A leírást a 13. lecke írja le.

Az Opciók [ListPlot3D] paranccsal megjelenítheti a funkciók teljes listáját, amelyek használatával módosíthatja a függvény grafikonjait.