Mi integráns, és miért kell ezt tudnom?
Képzeld el, hogy van valami függőség valamitől.
Így például, hogy nagyjából grafikusan ábrázolhatja a munkám sebességét, a napszaktól függően:
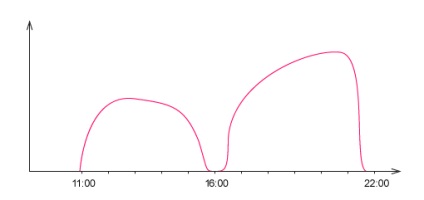
A sebességet a kódsorok percenkénti mérésével percenként, a valós életben programozó vagyok.
A munka mennyisége a munkamenet szorzata az idővel. Azaz, ha írok 3 vonal percenként, az óra kapjuk 180. Ha van egy ilyen táblázatot, akkor láthatod, hogy mennyi munka tettem a nap: ez az a terület, a diagram alatt. De hogyan számítható ki?
A gráfot egyforma szélességű oszlopokra osztjuk fel óránként. És ezeknek az oszlopoknak a magassága megegyezik a munka sebességével az óra közepén.
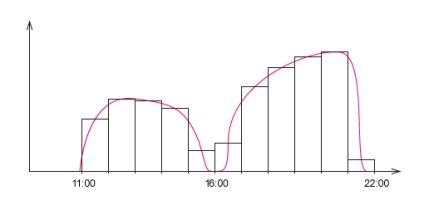
Az egyes oszlopok területét egyedileg lehet számolni, a szélességet magasságra kell szorozni. Kiderül, hogy az egyes oszlopok területe - ez az, hogy mennyire tettem minden órában a munkát. És ha összefoglalja az összes oszlopot, akkor a napi hozzávetőleges munkám.
A probléma az, hogy az eredmény közelítő lesz, de pontos számra van szükségünk. Fél óra múlva megtörjük a gráf oszlopokat:
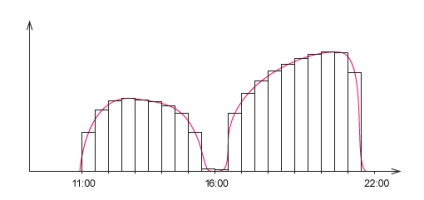
A kép azt mutatja, hogy ez sokkal közelebb áll ahhoz, amit keresünk.
Így a szegmensek csökkentése a grafikonon végtelenségig lehetséges, és minden egyes alkalommal közelebb és közelebb kerülünk az ütemterv szerinti területhez. És ha az oszlopok szélessége nullára növekszik, akkor területük összege a grafikon alatti területre irányul. Ezt az integráltnak nevezik, és így jelölik:
Ebben a képletben f (x) olyan függvénynek felel meg, amely az x értékétől függ, és az a és b betűk azok a szegmensek, amelyeken megtalálni az integrált értéket.
Miért szükséges ez?
A tudósok megpróbálnak minden fizikai jelenséget matematikai képlet formájában kifejezni. Ha van egy képletünk, akkor számíthatsz vele. És az integrál az egyik legfontosabb eszköz a funkciók kezeléséhez.
Például, ha van egy körképletünk, kiszámíthatjuk annak területét az integrál segítségével. Ha van egy labda formula, akkor kiszámíthatjuk a hangerőt. Az integráció, energia, munka, nyomás, tömeg, elektromos töltés és sok más mennyiség megtalálható.
Nem, miért van szükségem erre?
Igen, semmi - éppen ezért, a kíváncsiságtól. Tény, hogy az integrálások még az iskolai tantervben is szerepelnek, de nem annyira sok ember emlékszik arra, mi az.