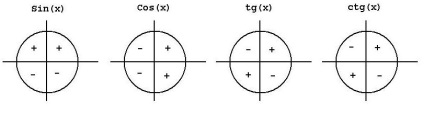
A szinusz, a koszinusz, a tangens és a cotangens tulajdonságai
legfontosabb nbsp> nbsp Wiki bemutató nbsp> nbsp Math nbsp> nbsp9 osztályban nbsp> nbsp A szinusz, a koszinusz, a tangens és a cotangent tulajdonságai
Sinus tulajdonságok
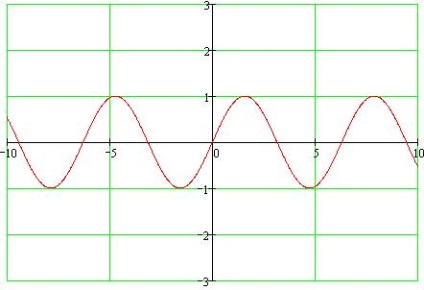
- 1. A meghatározás köre: az egész számozási tengely
- 2. Értéktartomány: [-1; 1]
- 3. A furcsa funkció.
- 4. A legkisebb pozitív idő: 2 * pi
- 5. A függvény gráfjának metszéspontjainak koordinátái az Ox tengelytől: (pi * n; 0)
- 6. A függvény görbéjének metszéspontjainak koordinátái az Oy tengelyével: (0; 0)
- 7. Az intervallumok, amelyeknél a függvény pozitív: (2 * pi * n; pi + 2 * pi * n)
- 8. Intervallumok, amelyeken a függvény negatív: (-pi + 2 * pi * n; 2 * pi * n)
- 9. A növekedési intervallumok: [-pi / 2 + 2 * pi * n; pi / 2 + 2 * pi * n]
- 10. A csökkenés intervalluma: [pi / 2 + 2 * pi * n; 3 * pi / 2 + 2 * pi * n]
- 11. A minimális pontok: -pi / 2 + 2 * pi * n
- 12. A funkció minimális értéke: -1
- 13. A maximális pontok: pi / 2 + 2 * pi * n
- 14. A funkció maximális értéke: 1
Cosine tulajdonságok
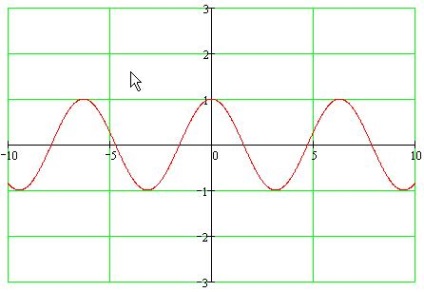
- 1. A meghatározás köre: az egész számtengely
- 2. Értéktartomány: [-1; 1]
- 3. Páros funkció.
- 4. A legkisebb pozitív idő: 2 * pi
- 5. A függvény gráfjának metszéspontjainak koordinátái az Ox tengelyével: (pi / 2 + pi * n; 0)
- 6. A függvény görbéjének metszéspontjainak koordinátái az Oy tengellyel: (0; 1)
- 7. Az intervallumok, amelyeknél a függvény pozitív: (-pi / 2 + 2 * pi * n; pi / 2 + 2 * pi * n)
- 8. Az intervallumok, amelyeknél a függvény negatív: (pi / 2 + 2 * pi * n; 3 * pi / 2 + 2 * pi * n)
- 9. A növekedés hézagai: [-pi + 2 * pi * n; 2 * pi * n]
- 10. A csökkenés intervalluma: [2 * pi * n; pi + 2 * pi * n]
- 11. A minimális pontok: pi + 2 * pi * n
- 12. A funkció minimális értéke: -1
- 13. Maximális pontok: 2 * pi * n
- 14. A funkció maximális értéke: 1
Az érintő tulajdonságai
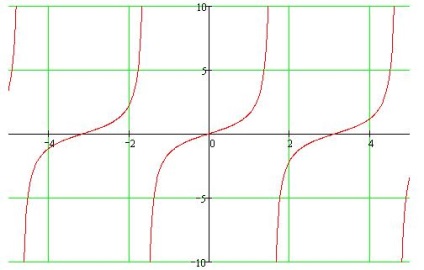
- 1. A meghatározás területe: (-pi / 2 + pi * n; pi / 2 + pi * n)
- 2. Értékek terjedelme: az egész numerikus tengely
- 3. A furcsa funkció.
- 4. A legkisebb pozitív időszak: pi
- 5. A függvény gráfjának metszéspontjainak koordinátái az Ox tengelytől: (pi * n; 0)
- 6. A függvény görbéjének metszéspontjainak koordinátái az Oy tengelyével: (0; 0)
- 7. Az intervallumok, amelyeknél a függvény pozitív: (pi * n; pi / 2 + pi * n)
- 8. Intervallumok, amelyeken a függvény negatív: (-pi / 2 + pi * n; pi * n)
- 9. A függvény növekszik az intervallumokban (-pi / 2 + pi * n; pi / 2 + pi * n)
- 10. Nincsenek magas és alacsony pontok.
Cotangent tulajdonságok
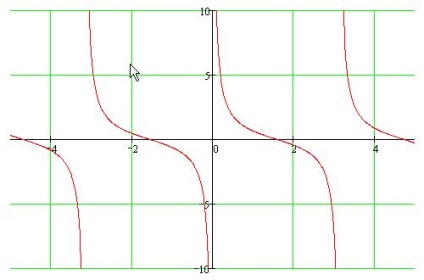
- 1. A meghatározás területe: (pi * n; pi + pi * n)
- 2. Értékek terjedelme: az egész numerikus tengely
- 3. A furcsa funkció.
- 4. A legkisebb pozitív időszak: pi
- 5. A függvény gráfjának metszéspontjainak koordinátái az Ox tengelyével: (pi / 2 + pi * n; 0)
- 6. A funkciógörbe metszéspontjainak koordinátái az Oy tengelyével: No.
- 7. Az intervallumok, amelyeknél a függvény pozitív: (pi * n; pi / 2 + pi * n)
- 8. Intervallumok, amelyeken a függvény negatív: (-pi / 2 + pi * n; pi * n)
- 9. A függvény időközönként csökken (pi * n; pi + pi * n)
- 10. Nincsenek magas és alacsony pontok.
Az alábbi ábrán több egykörös kör látható, amelyekben a szinusz, a koszinusz, a tangens és a cotangens jelek különböző koordinátarendszerekben jelennek meg.