Kartográfiai előrejelzések 1
CARTOGRAPHIC PROJECTIONS, matematikai módszerek a Föld ellipszoid teljes felületének vagy annak részének a térkép síkjára történő leképezésére. A térképi vetületek a térképen a pontok geodetikai koordinátáit (B szélesség és L hosszúság) és a téglalap alakú koordináta (X és Y) között egyeznek meg:
Az f1 funkciók konkrét megvalósítása. és f2 gyakran összetett, számuk végtelen, ezért a kartográfiai előrejelzések sokfélesége korlátlan. A kartográfiai vetületek kezdeti axiómája, hogy a gömbfelület nem hajtható le a síkban deformációk, összehúzódások és törzsek nélkül, nagyságrenddel és irányban eltérően. A matematikai térképészet mindenfajta torzítást tanulmányoz, és olyan módszereket dolgoz ki, amelyekben a torzítások a legkisebb (bizonyos értelemben vett) értékeket vagy előre meghatározott eloszlást eredményeznék. A különböző térképészeti vetületek a következő típusú torzítással rendelkezhetnek: Hosszú torzítások - a hosszúságok és távolságok skála instabil a térkép különböző pontjain és különböző irányokban; a területek torzítása - a térkép különböző pontjain lévő területek mértéke eltérő, ami megtöri a tárgyak méretét; Sarok torzulások - a térképen lévő irányok közötti szögek torzulnak a terepen lévő sarkokhoz képest; alakzatok torzulása - a térképen lévő ábrák deformálódnak, és nem hasonlítanak a terepen lévő ábrákhoz, ami a sarkok torzulásának következménye.
Mindenesetre vetületi megkülönböztetni főskála hosszúságban és területeken - az arány jelzi az csökkentés mértékét az ellipszoid mérete (gömb), tekintettel a képet a térképen és részleges mértékben - az arány a infinitezimális intervallum (vagy térben), ábrázolt a térképen a megfelelő infinitezimális érték ellipszoid (golyó). Kartográfiai animációk is időskála t. E. Az arány a kártyák demonstrációs időt a valós idejű, a képalkotás.
Természete által torzítás felmerülő az átmenet a gömbfelület egy síkban vetülettani oszlanak egyenlő, amelyek megtartják a tér méretei, konform, nem hagyva torzítás szögek és formájú kontúrok (korábbi néven őket konform) és önkényes, ahol a hely és szögeket ferde különböző arányok. Speciális esete a tetszőleges vetületi - egyenlő távolságra vetítés, ahol a skála állandó az egyik fő terület (meridián vagy párhuzamos). Lásd: Projections Maps.
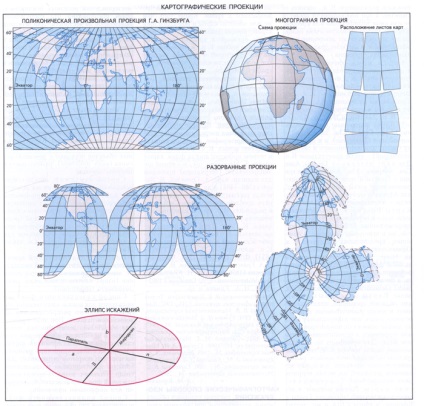
Mérjük deformációk a vetületi ellipszis torzítás (vagy Tissot mutatószám). Bármilyen végtelenül kerülete a világon (ellipszoid) jelenik meg a térképen végtelenül ellipszis méretét és alakját, amely tükrözi a torzítás hosszúságú, területek és szögek. A hossza és orientációja a nagytengely iránya egyeznie a maximális torzítás nyújtás (a) egy adott ponton, és a kistengely - maximális összehúzódást (b), a szegmensek mentén, a meridián és párhuzamos jellemzésére részleges mértékben ezek mentén (m és n).
A térképek torzulása speciális izolinok - isokol, azaz egyenlõ torzítású vonalak, területek, szögek vagy alakzatok segítségével is kimutatható.
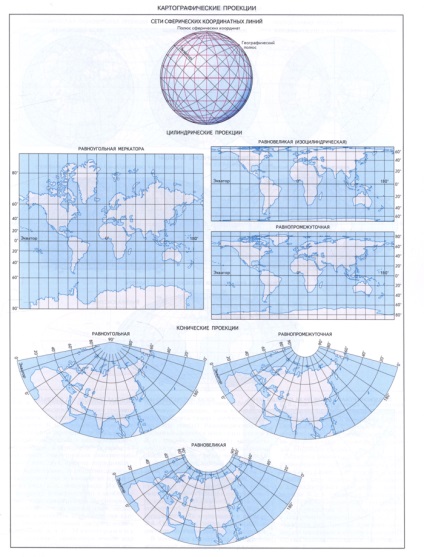
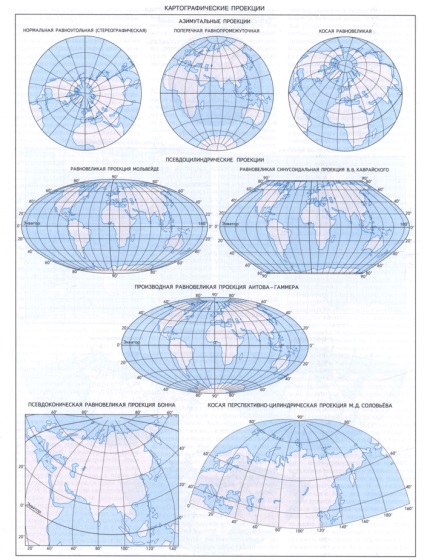
Attól függően, hogy a pozíció tengelyen, használt rendszer megtervezésénél gömbi koordináták, megkülönböztetni vetülettani normál (gömbi koordináta tengely egybeesik a Föld forgástengelyének), keresztirányú (gömbi koordináta tengely síkjában fekszik szélesség) és a ferde (gömbi koordináta tengelyt szögben az egyenlítői síkkal ).
Hivatkozva a normál rács meridiánok és szélességi izoláljuk hengeres vetületi amelyben szélességi és hosszúsági körök a szokásos rács egyenes, kölcsönösen merőleges vonalak; más szavakkal, a világon (ellipszoid), ahogy ez vetítik alátámasztó felületre érintőleges vagy szelő hengert, amelyet azután kibontakozott síkba. A kúpos térképi vetülete a felület a földgömb is vetítik alátámasztó felületre érintőleges vagy szekáns kúp, így a normál kúpvetület meridiánok - egyenes, érkező a pole pont, és párhuzamos - ívek a koncentrikus körök. A normál (poláros) azimutális vetületi felülete a világon átkerül a kisegítő merőleges síkban a forgástengellyel párhuzamosan rá - koncentrikus körök, és meridiánok - átmérők e körök. Ebben a vetületben a poláris régiókat mindig leképezik. Ha a sík vetülete síkjára merőleges az egyenlítőtől, kiderül oldalsó (egyenlítői) azimut vetítés, amely mindig használható térképeket a félgömbön. Kiegészítő érintőleges felületek, így a közös vonal vagy pont egy ellipszoid (labda), és a gép a kártyát, ahol torzítás nélkül. Szegélyes felület esetén két közös vonal jelenik meg. Ezzel párhuzamosan Pseudocylindrical vetülettani - közvetlen (mint a hengeres nyúlványok), a középső meridián - azokra merőleges egyenes és a másik meridiánok - görbék, növelve a görbület a távolság a központi meridián. A psevdokonicheskih vetülettani tűnik az összes párhuzamos ív koncentrikus körök (ahogy ez a szokásos kúp), a középső meridián - egy egyenes vonal, és a többi a meridiánok - a görbék, azok görbületi növekszik távolság a központi meridián. Normális polikonikus vetülettani bemutatott párhuzamos ív excentrikus körök és hosszúsági - görbék, szimmetrikus közvetlen központi meridián. Polar psevdoazimutalnye Vetülettan - ez egy módosított azimutális vetítés, amely párhuzamos ábrázoltuk koncentrikus körök, és meridiánok - formájában görbék, szimmetrikus egy vagy két egyenes meridiánok.
A számítógépes technológiák lehetővé teszik, hogy ezeket és sok tetszőleges kartográfiai előrejelzést bármilyen módon megkapják. Tulajdonságaik a térképes terület és a globális helyzetének megfelelően vannak meghatározva, a térkép használatának célját és módját, a torzítások előnyben részesített eloszlását és hasonlókat. Sokrétű kartográfiai vetületeket kapunk, ha a gömböt egy poliéder felületére vetítjük. Leggyakrabban minden oldal egy egyenlő oldalú trapéz, bár más változatok is lehetségesek (például hatszögek, négyzetek, rombuszok). A sokoldalú többsávos kartográfiai vetületek, és a sávok "vághatók" a meridiánok mentén és párhuzamosan. Az ilyen kivetítések kényelmesek, mivel az egyes arcokon vagy szalagon belüli torzítások kicsiek, ezért mindig többlevelű térképekhez használják őket. A topográfiai és felmérési topográfiai térképek kizárólag egy polyhedrikus vetületben jönnek létre, és az egyes lapok kerete egy szférikus trapéz alakú, amely a meridiánok és a párhuzamok soraiból áll. Azonban a térképek blokkja nem kombinálható közös keretek között szünetek nélkül.
A nagy számú vetületi oka, hogy a különböző feladatokat, amelyek a kártyákat (például a tengeri és a légiforgalmi térképek szükséges konform és kataszteri mérések - az egyenlő térképi vetület), a földrajzi elhelyezkedés, a terület (a sarki régiókat mutat normál térkép előrejelzések, és a félgömb - egy cross-azimut a vetületek), kinevezés kártyák (különböző vetítési igényeit az iskolai és tudományos referencia kártya). Alkotó speciális elektronikus atlaszok Vetülettan, amellyel megtalálja a megfelelő vetületi, hogy értékelje annak tulajdonságait, és tartsa azokat, vagy más módosítása vagy átalakítása, ha szükséges. A lehetőségek széles választéka nagyon nagy, de vannak még néhány kedvelt és leginkább hagyományos térképészeti vetület.
A világtérképek általában hengeres, pszeudocylindrikus és polikonikus térképkialakításokból állnak. Hogy csökkentse a torzítás gyakran metsző hengerek és Pseudocylindrical térképi vetülete adott szünetekkel az óceánokban. A félgömbök térképei mindig az azimutális térképező vetületekből állnak. laterális (egyenlítői) használtunk a nyugati és keleti félteke az északi és a déli féltekén - normál (poláris), más esetekben (pl a kontinentális és óceáni féltekén) - ferde azimut vetületek. Mert térképeket a kontinensek, Európa, Ázsia, Észak-Amerika, Dél-Amerika, Ausztrália és Óceánia a leggyakrabban használt egyenlő ferde azimutáiis vetülettani for Africa - a keresztet, és az Antarktisz - normál azimut vetületek. Oroszország kártyák általában teszik ki leggyakrabban a szokásos kúp egyenlő távolságra vetülettani a szelő kúp, de bizonyos esetekben - a polikonikus, önkényes és egyéb vetületek. Azonban a kúpos térképkialakítások rács nem mindig megfelelő. Például az orosz térképek általános iskola köteles vetület, ahol a meridiánok konvergál a pólusok, és a legészakibb pontja a föld (Cape Chelyuskin) legközelebb eső az északi határon. Térképek az egyes országok közigazgatási régiók, tartományok, államok végre a ferde konform és egyenlő kúp vagy azimut vetületi, de sok múlik a konfiguráció a területen is, és a helyét a világon. Kis területeken a feladatot területek kiválasztására térképvetületekről elveszíti relevanciáját, lehetséges, hogy különböző konform előrejelzések, mivel a területek torzítás kis területen malooschutimy. A topográfiai térképek Oroszország hozzon létre egy kereszt alakú Gauss - Krüger és térképek az USA és számos más nyugati országokban - az Általános Mercator henger alakú kiemelkedést (rövidítve UTM). Mindkét vetület közel áll a tulajdonságaihoz, és mindkettő alapvetően több sávú. Tengeri és légi térképek kivételes teljesítményt egy hengeres nyúlvány Mercator és tematikus térképek a tengerek és óceánok nyújtanak sokféle néha meglehetősen bonyolult előrejelzések. Például a közös kiállítás az Atlanti-óceán és a Jeges használt különleges vetítési izokolami ovális, és a kép az óceánok - az egyenlő vetítés hézagokkal a kontinensen.
Mindenesetre, a választás a vetítés, különösen a tematikus térképek, meg kell jegyezni, hogy általában minimális torzítás a térképen a központban, és gyorsan növekszik a szélek felé. Ezen túlmenően, a kisebb léptékű, a térképek és a részletes térbeli lefedettség, annál nagyobb figyelmet kell fordítani a matematikai tényezők megválasztása térkép előrejelzések, és fordítva, kis területekre és nagyléptékű egyre jelentősebb földrajzi tényezők.
Rövid történelmi információk. Az első térképeket meridiánok és párhuzamokat használó görög tudósok, Eratosthenes, Hipparchus hozta létre. Claudius Ptolemy írta le a "földrajzi útmutató" néhány kúpos előrejelzésének elveit. Nagy földrajzi felfedezések a térképészet jelentős fejlődésének szolgálták, és hozzájárultak az új kartográfiai előrejelzések megteremtéséhez. A nagy hozzájárulása az elméleti előrejelzések által flamand térképész :. G. Mercator, aki egy hengeres (Mercator) vetítés navigációs térképek, Ortelius A., J. Jansson (1588-1664) stb Az elmélet vetítés úgy tartják számon, mint a legfontosabb tudományos feltérképezése probléma. Hozzájárulnak a térképvetületekről készült híres matematikus I. Lambert, Euler, Lagrange, Gauss. A 19. század közepén a francia kutató A. Tissot a kartográfiai előrejelzések torzításainak általános elmélete volt. Oroszországban, az elmélet a térkép nyúlványok részt AP Bolotov (1803-1853), F. Schubert, Csebisev, DA Grave, Dmitry Mengyelejev, V. Witkowski (1856-1924 ), FN Krasovskiy, VV Kavraiskii, G. A. Ginzburg (1905-1975), N. A. és munkatársai Urman.