A Mobius örvénylapja
A Wikipédiából, a szabad enciklopédiából

Möbius-szalag (Möbius sávban, Mobius hurok) -topologicheskiyobekt, prosteyshayaneorientiruemayapoverhnosts él-oldalú beruházással a szokásos trohmernoeevklidovo prostranstvoR³. A felület egyik pontjáról bármilyen más felületre juthat anélkül, hogy átlépné a széleket.
2 Geometria és topológia
5Art és technológia
6Mobius zenekar és végtelen jel
Ha vágni a szalagot egy vonal mentén egyenlő távolságra a szélek helyett két Möbius sáv kap egy hosszú kétoldalas (kétszer csavart, mint a Möbius-szalag) frekvenciasávban, amely az úgynevezett „Afganisztán szalag”. Ha most levágja ezt a szalagot a közepén, két szalagot kapsz egymás köré.
Ha megvágja a Möbius, onnan a szélén mintegy egyharmada a szélessége, megkapjuk a két szalag, az egyik - vékonyabb Möbius-szalag, a másik - egy hosszú csík két fél fordulattal (afgán szalag).
A szalagok más érdekes kombinációi két vagy több fél fordulattal rendelkező szalagokból is beszerezhetők. Például, ha három féle fordulattal szalagot vágsz, kapsz egy szalagot, egy sárgabarack gömbölyű borotváját. A szalag további kanyarokkal történő bemetszése váratlan alakokat eredményez, az úgynevezett parafmikus gyűrűk.
Geometria és topológia
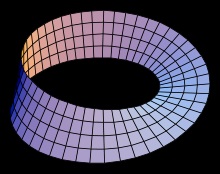
A Möbius leaf paraméteres leírása.
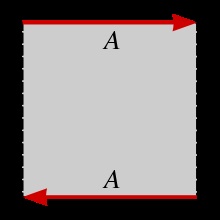
A négyzetet Mobius lapra forgatva csatlakoztassa a megjelölt éleket úgy, hogy a nyilak iránya egybeessen.
Az egyik módja annak, hogy egy Mobius csíkot mutassanak be részhalmazként a parametrizáció:
hol és. Ezek a képletek meghatározzák az 1. szélességű Möbius-csíkot, amelynek központi körének 1. sugara a középső b xy-központjában van. A paraméter a szalag mentén halad, míg a széltől a távolság határozható meg.
A hengeres koordinátákban a Mobius szalag korlátlan változata az alábbi egyenlettel ábrázolható:
A topológiai Mobius lehet egy négyzet tér az egyenértékűség szempontjából.
A Mobius szalag egy nem irányítható felületi felület.
A Móbius szalag egy nem triviális köteg helyszíne is egy körön vágott vonallal.
Hasonló tárgyak
Egy közeli "furcsa" geometriai tárgy a Klein palack. A Klein palack két Möbius-sáv ragasztásával érhető el. A szokásos háromdimenziós térben ez nem lehetséges, anélkül, hogy saját kereszteződést hozna létre.
Egy másik hasonló készlet egy filmes gömb. Ha a szférában lyukasztja a lyukat egy filmmel, akkor a maradék Mobius szalag lesz. Másrészt, ha lemezt ragaszt a Möbius szalaghoz, a határaik ötvözésével, az eredmény egy gömb lesz egy filmmel. Ennek felismerése érdekében hasznos a Möbius-sáv deformálódása, úgy, hogy a határa közönséges körré váljon. Ezt a számot "keresztre feszített fedőnek" nevezik (egy átfedő fedél ugyanazt a számot jelentheti egy ragasztott lemezzel, vagyis a projektív sík bemerítésével).
Általános félreértés van, hogy egy keresztezett fedelet nem lehet három dimenzióban kialakítani önzáró felület nélkül. Valójában lehetséges a Mobius szalagot elhelyezni az ideális körhatárral. Az ötlet a következő: vesszük fontolóra a kör alakú kört a síkban. Soedinivantipodnyetochki mindannyian, hogy ez az a pont, uglamiθiθ + πdugoy kör, azt találjuk, hogy dlyaθmezhdu0iπ / 2dugi fölött fekszenek ploskostixy és drugihθnizhe (és két helyen ív hazugság ploskostixy).
Megjegyezhető, hogy ha a lemezt ragasztják a határoló körhöz, akkor az eredményül kapott gömb és a film öncsomópontja elkerülhetetlen háromdimenziós térben. A négyzet oldalainak meghatározása tekintetében, amint azt fentebb bemutattuk, a gömböt a filmből úgy kapjuk meg, hogy ragasztjuk a két fennmaradó oldalt az orientáció megőrzésével.