A laboratóriumi munkába való felvétel
A laboratóriumi munka elkezdéséhez először be kell szereznie a tanár felvételét, amely az óra után szükséges:
Figyelmesen olvassa el a munka irányelveit.
A munkaismeret elsajátításához szükséges elméleti anyag tanulmányozása. Szükség esetén további szakirodalom tanulmányozása (az irodalmi források listája csatolt).
A lecke elkészítésekor ismerkedjen meg a laboratóriumi felszereléssel, megtudja, mit és mit mérjen.
Egy auditorium laborban bejuthat a tanárhoz.
Hogyan szervezzen laboratóriumi munkát?
Címlap: Az RK Oktatási és Tudományügyi Minisztériuma, a YuKU Állami Egyetem neve. M.Auezova, "Fizika" osztály, a laboratóriumi munka neve és száma, a hallgató teljes neve, csoport, a tanár teljes neve, város, év.
Az iránymutatások szövegének Xerox letapogatása nem megengedett.
Ha grafikát kell készíteni a munkádra, akkor azt milliméteres papírra kell vinni.
Laboratóriumi munka védelme és értékelése
A laboratóriumi munka védelme érdekében írásos és szóbeli jelentést kell adnia a tanárnak a munkáról. A laboratóriumi munka maximális pontszámát (lásd tantervet) a diáknak kell kitéve, ha:
A diák teljes egészében elvégezte a munkát.
A hallgató tudja, hogy a munka, a laboratóriumi felszerelés, a technika és a szerszámok megmutatják, hogyan végezte a munkát, mit és hogyan mért.
A hallgató teljes és helyes választ ad a kontroll kérdésekre.
A laboratóriumi munka minimális pontszámát (lásd a tantervet) a diáknak mutatják be, ha teljes egészében elvégezte a munkát, helyesen megtervezte, de a védelem alatt csak írásbeli jelentést nyújtott be.
Laboratóriumi munka száma 1. A közvetlen mérések eredményeinek matematikai feldolgozása
Célok és célkitűzések: Értékelje a feldolgozási eljárásának eredményét közvetlen méréseket többszörös adatmérési például egy matematikai inga oszcilláció időszakban meghatározni a legvalószínűbb érték és a mért értékek, standard eltérés, konfidencia intervallum egy adott nadezhnosti
Az emberi érzékelések és mérőeszközök tökéletlenségei miatti mérések pontatlanságokkal járnak. Az összes mérést lehetővé teszik bizonyos hibák a mérési eredmények lehetővé teszik számunkra, nem igaz, de csak közelítő értéket mért velichiny létesítése megengedett mérési hiba a tartomány, amelyben fekszik a valódi értéke a mérendő, és előfeltétele a megbízhatóság eksperimenta mérési hibák osztva a kombiné és szintén szisztematikus és véletlenszerű hibák
Csúszások miatt meghibásodást a készülék vagy figyelmetlenség megfigyelő, megsérti a kísérleti eljárás feltételeit, illetve a saját provedeniya A legtöbb esetben csúszik szembetűnő, mivel összeillik minták nagymértékben különböznek az ilyen mérési eredmény otschetov tartalmazó csúszás, nem lehet figyelembe venni az adatok feldolgozása - az egyszerűen el kell dobni
Szisztematikus hibák által okozott hibák és pontatlanságok kalibrációs mérőműszerek, ha azt a pontatlan adatok kiszámítása, és azért is, mert a hiányosságokat a módszer izmereniya Ezek a hibák befolyásolják a mérési eredményeket mindig odnostoronne Nyilvánvaló, hogy a hatás a rendszeres hibák nem lehet csökkenteni számának növelésével izmereniy Azonban, ha jellegét és tulajdonságait a rendszeres hibák ismertek, ezek hatása a mérési eredményt lehet elszámolni által bevezetett módosítások és hagyni.
Véletlen hibák okozta ingadozások és a mért értékek, a megjelenés nem lehet megakadályozni, így azok valamilyen hatással van az egyes mérési eredmény változó mindkét irányban, azaz mind növelni vagy csökkenteni ih Úgy tartsa be a törvényeket a statisztika, így a hatás véletlenszerű hibák a mérési eredmény lehet elszámolni, vagy jelentősen umenshit alkalmazva valószínűség törvényei, a legvalószínűbb meghatározni a mért értékek és a lehetséges eltéréseket ezeket az értékeket.
Engedje meg, amikor ismételten megmértünk egy bizonyos fizikai mennyiséget

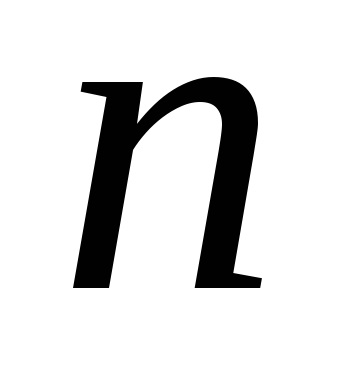
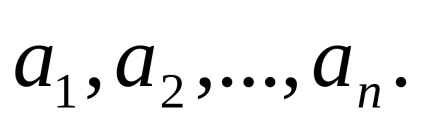
Minden egyes mérés eltér a számtani átlagtól

eltérés
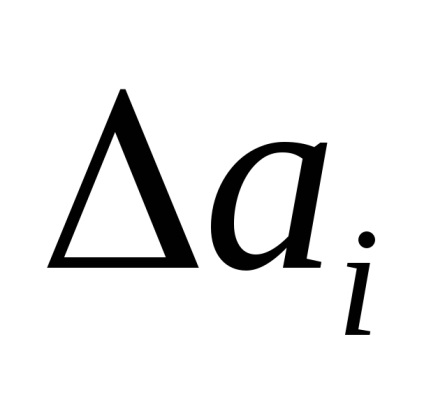
Tapasztalatból tudjuk: minél nagyobb a hiba, a valószínűsége annak megnyilvánulása menshe Ezen felül, ha a mérések száma igen nagy, a hibák, azonos nagyságú, de ellenkező előjellel, de egyformán chasto Fast csökkenti a valószínűségét a hiba
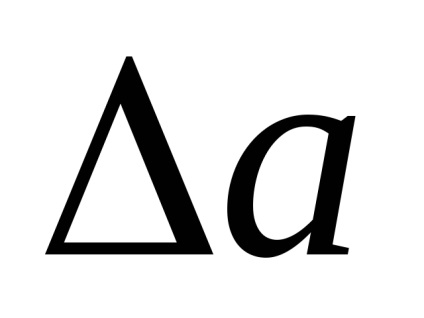
Minél kisebb a variancia, annál kisebb egy nagyobb véletlen hiba valószínűsége és kisebb az egyedi értékek terjedése
A mérési variancia négyzetgyöke az átlagos négyzetes hiba
Ha helyett
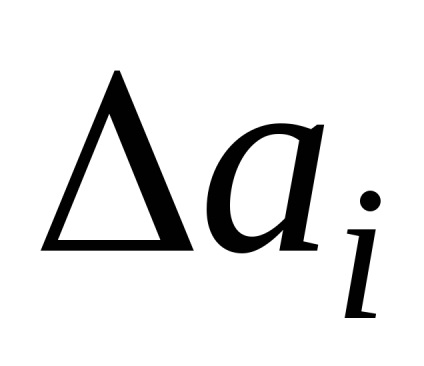
A kifejezés (1.1.7) tartalmazza a mennyiséget

A variancia becslései
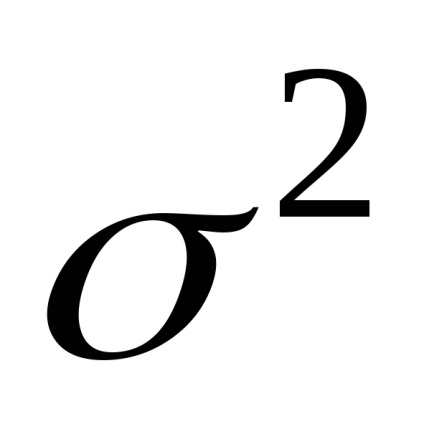
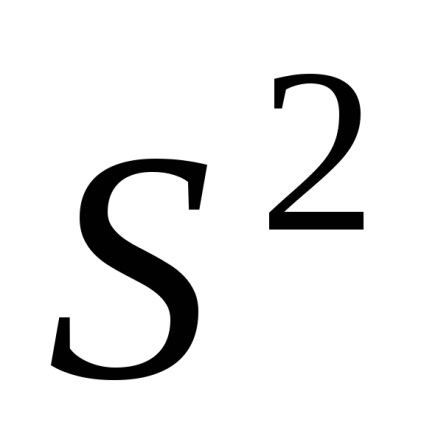
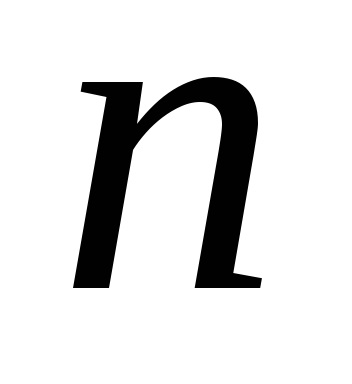
A mérések feldolgozásának feladata meghatározni az intervallumot
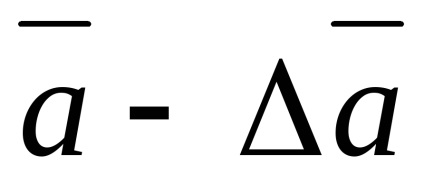

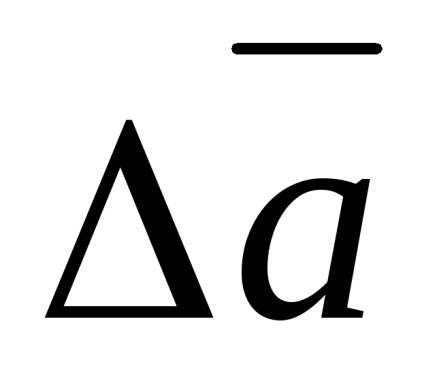

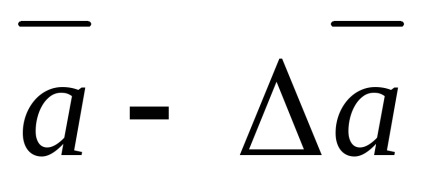
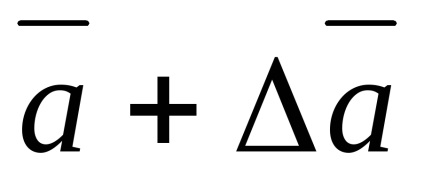

Ha a mérések száma elég nagy, akkor a konfidencia valószínűsége a teljes mérési szám azon töredékét fejezi ki, amelyben a mért érték a konfidenciaintervallumon belül van, például ha 100 mérést végeznek,
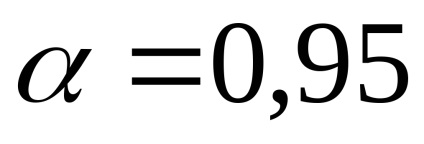
A hibák elméletéből következik, hogy számos mérésnél (több mint száz kísérletnél) az intervallum konfidencia valószínűsége
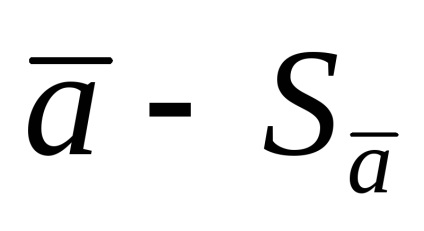
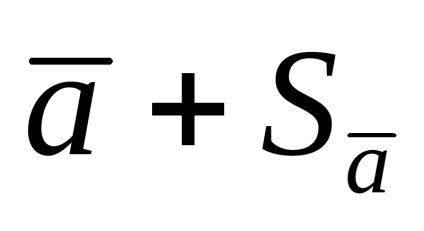
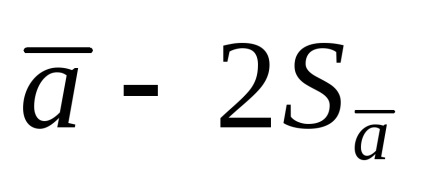
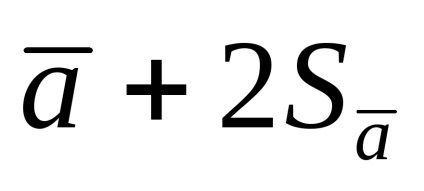
Azokban az esetekben, amikor a mérések száma kicsi, a véletlenszerű hibák meghatározásának alapjául szolgáló statisztikai szabályszerűségek szigorú megnyilvánulására nincsenek feltételek, ami a középértéktől való szórás eltérését jelenti. (1.1.9.) alapján számított, pontatlan, és a pontatlanság nagyobb, annál kisebb a mérések száma.
Ezért annak érdekében, hogy a mért mennyiség valós értéke egy adott valószínűséggel a konfidencia intervallumon belül legyen, az utóbbit meg kell növelni, korlátozott számú mérés esetén a Sa nem tekinthető a konfidenciaintervallum határának. és a következő érték:
A számérték
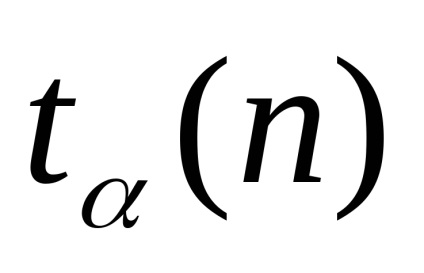
A mérési eredmények az eltérő értékek nem lehet összehasonlítani egymással az abszolút oshibkam Összehasonlításképpen, a mérési pontosság az ilyen mennyiségek a relatív hiba kerül bevezetésre - az arány az abszolút hiba a középértékhez a mért velichiny
Relatív hiba esetén célszerű összehasonlítani a homogén mennyiségek mérési eredményeit
Berendezés: matematikai inga, stopper.
A munka sorrendje:
Mérjük meg az inga 20-30 oszcillációjának időtartamát (az inga N oszcillációinak számát a tanár állítja be) • Ismételje meg az n-t (a kísérletek n száma a tanár által állítható)
Minden egyes kísérletnél meg kell találni az inga ingadozásának időtartamát az alábbi képlet szerint:
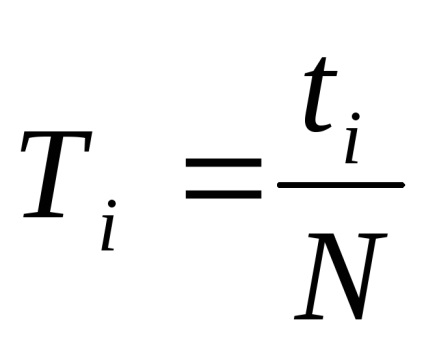
Határozzuk meg az inga oszcillációs periódusának átlagos számtani értékét a képlet szerint:
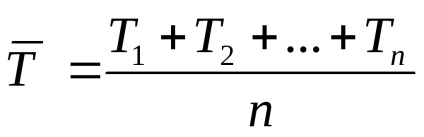
Keresse meg az egyes kísérletekhez tartozó értékeket
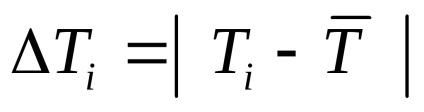
egyenesen
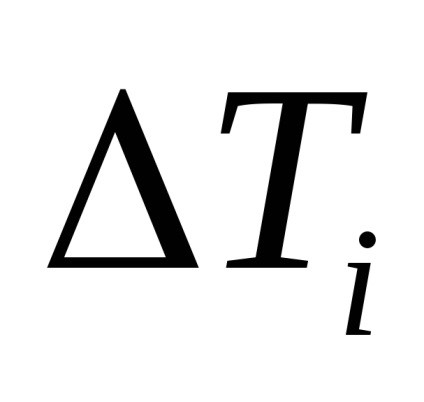
Keresse meg az oszcillációs periódus szórását a következő képlet segítségével:
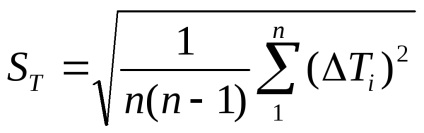
A laboratóriumban rendelkezésre álló táblázat szerint keresse meg a tanulói együttható értékét, amely megfelel a tanár megbízhatóságának és a kísérletek számának.
Számolja ki a mérések abszolút hibáját a következő képlet segítségével:
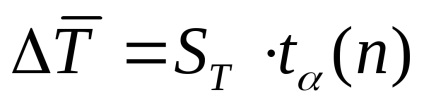
Számítsa ki a relatív hibát a képlet segítségével
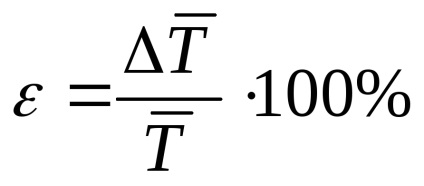
A mérések és számítások eredményeit a táblázatba kell beírni: